Advances in Applied Mathematics
Vol.
09
No.
02
(
2020
), Article ID:
34280
,
7
pages
10.12677/AAM.2020.92028
Approximation Properties of Bivariate (p, q)-Bernstein Operators
Pan Gao, HuiHui Liu, Xianxiang Leng
School of Mathematics and Statistics, Chaohu University, Hefei Anhui
Received: Feb. 2nd, 2020; accepted: Feb. 17th, 2020; published: Feb. 24th, 2020

ABSTRACT
In this paper, we introduce the bivariate (p, q)-Bernstein operator on the basis of (p, q)-Bernstein operator, and obtain the approximation theorem of the operator. The uniform convergence of the operator is verified by applying Volkov theorem, and its convergence rate is estimated. Those results further promote some of the conclusions of (p, q)-Bernstein operator.
Keywords:Bivariate (p, q)-Bernstein Operators, Rate of Convergence, Lipschitz Function

二元(p, q)-Bernstein算子的逼近性质
高盼,刘辉辉,冷献祥
巢湖学院数学与统计学院,安徽 合肥

收稿日期:2020年2月2日;录用日期:2020年2月17日;发布日期:2020年2月24日

摘 要
本文在(p, q)-Bernstein算子的基础上构建二元(p, q)-Bernstein算子,证明该算子的逼近定理;应用Volkov定理验证了该算子的一致收敛性,并估计其收敛速度,此结论推广了一元(p, q)-Bernstein算子的逼近结果。
关键词 :二元(p, q)-Bernstein算子,收敛速度,Lipschitz函数

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
算子是逼近理论重要的研究对象,其中经典的算子之一为Bernstein算子。最早于1912年,Bernstein首次提出。其后,众多研究者开始关注研究Bernstein算子的推广。于是,Bernstein算子的各种变形算子纷纷被讨论,如Szász-Mirakjan-Kantorovich算子 [1],Baskakov算子 [2] 等。
随着数学与生产生活各领域的交错发展,学者们将q微积分引入逼近理论,构造出大量q型算子。2007年,Dalmanoglu Ö. [3] 研究了q-Bernstein-Kantorovich算子;2011年,Muraru C V [4] 提出q-Bernstein-Schurer算子,并研究其逼近问题;伴随着研究的进一步深化,二元或多元算子相继被提出,故得到了大量二元算子关于逼近的相关理论,详见文献 [5] [6] [7] 等。
q微积分在逼近中的发展推动了(p, q)微分学步入逼近理论。Mursaleen于2015年首次在q-Bernstein算子的基础上提出(p, q)-Bernstein算子 [8],实现了q-Bernstein算子性质的推广。自此,有关于(p, q)型算子呈现于世人面前。2016年,Acar在文献 [9] 中构建了两元(p, q)-Bernstein-Kantorovich算子并证明该算子一些的逼近结论。由此可知,关于(p, q)型二元算子逼近问题的研究正在持续发展中。本文构建出二元(p, q)Bernstein算子,证明算子的一些逼近相关的定理,从而更进一步推广一元算子的逼近性质,更加丰富逼近理论的完整性。
2. 知识储备
下文中出现的符号:
主要定义为:
定义1 [8] :设
,,,则(p, q)-Bernstein算子定义为下式:
其中
。
定义2:设
,,定义二元(p, q)-Bernstein算子为:
其中
引理1 [8] :设
,,则有
引理2:设
,,,(
为正整数),则有下列等式成立:
证明:根据算子定义式与引理1,计算可得
同理可证出
;
,故引理成立。
引理3:设
,,则有下列等式成立:
证明:根据引理2与算子的线性性质易得结论。
3. 主要结果
首先介绍一些记号:设
,,,则关于f的连续性模可以表示为:
;
并且
满足以下性质:
阶Lipschitz条件的二元函数f:对于
,,,则存在常数
,使得
;记为
。
定理1:若
,且
,,则对于
,都有
。
证明:根据引理2得到
又因为当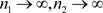 时,
时,
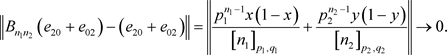
故根据Volkov定理的内容可以得到 。
。
定理2:若 ,有不等式
,有不等式

其中 。
。
证明:根据二元函数连续模的性质,则有
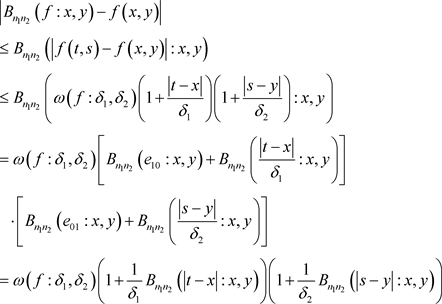
又利用Cauchy-Schwarz不等式与引理3,有


因此,得到

取 ,即
,即 成立。
成立。
定理3:设 且
且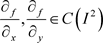 ,则有
,则有
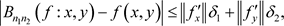
其中
证明:因为 ,可得
,可得
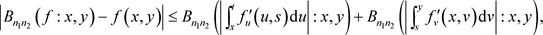
又因为
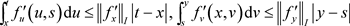
利用算子作用与柯西–施瓦茨不等式计算有

定理4:若 ,则存在一个常数
,则存在一个常数 ,有下式成立:
,有下式成立:

其中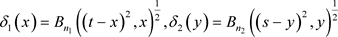 。
。
证明:由 ,计算可得
,计算可得
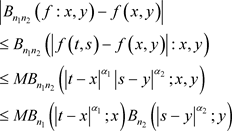
利用Hölder不等式,取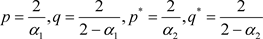
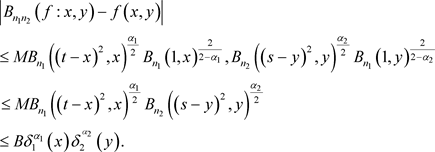
取 即定理成立。
即定理成立。
致谢
本文的写作感谢查星星老师的指导。
基金项目
巢湖学院国家级大学生创新创业训练计划资助项目(201910380035),巢湖学院省级大学生创新创业训练计划资助项目(S201910380068)。
文章引用
高 盼,刘辉辉,冷献祥. 二元(p, q)-Bernstein算子的逼近性质
Approximation Properties of Bivariate (p, q)-Bernstein Operators[J]. 应用数学进展, 2020, 09(02): 244-250. https://doi.org/10.12677/AAM.2020.92028
参考文献
- 1. Totik, V. (1983) Approximation by Szász-Mirakjan-Kantorovich Operators in Lp (p > 1). Analysis Mathematica, 9, 147-167. https://doi.org/10.1007/BF01982010
- 2. Pethe, S. (1984) On the Baskakov Operator. Indian Journal of Mathematics, 26, 43-48.
- 3. Dalmanoglu, Ö. (2007) Approximation by Kantorovich Type q-Bernstein Operators. Proceedings of the 12th WSEAS International Conference on Applied Mathematics, Cairo, Egypt, 29-31 December 2007, 113-117.
- 4. Muraru, C.V. (2011) Note on q-Bernstein-Schurer Operators. Studia Universitatis Babes-Bolyai Mathematica, 56, 489-495.
- 5. Simeonov, P. and Zafiris, V. (2008) Geometric Applications of Bivariate q-Bernstein and q-Orthogonal Polynomials. American Conference on Applied Mathematics, 3, 25-28.
- 6. Agrawal, P.N., Finta, Z. and Kumar, A.S. (2015) Bivariate q-Bernstein-Schurer-Kantorovich Operators. Results in Mathematics, 67, 365-380. https://doi.org/10.1007/s00025-014-0417-z
- 7. Pop, O.T. and Fărcaş, M.D. (2009) About the Bivariate Operators of Durrmeyer-Type. Demonstratio Mathematica, 42, 97-107. https://doi.org/10.1515/dema-2009-0110
- 8. Mursaleen, M., Ansari. K.J. and Khan, A. (2016) Erratum to “On (p, q)-Analogue of Bernstein Operators [Appl. Math. Comput. 266 (2015) 874-882]. Applied Mathematics and Computation, 278, 70-71.
https://doi.org/10.1016/j.amc.2016.02.008
- 9. Acar, T., Aral, A. and Mohiuddine, S.A. (2016) Approximation by Bivariate (p, q)-Bernstein-Kantorovich Operators. Iranian Journal of Science and Technology, Transactions A: Science, 42, 655-662.
https://doi.org/10.1007/s40995-016-0045-4







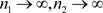 时,
时,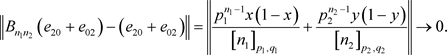
 。
。 ,有不等式
,有不等式
 。
。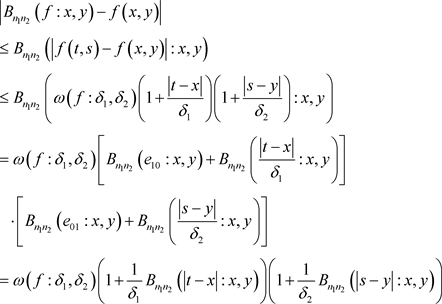



 ,即
,即 成立。
成立。 且
且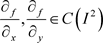 ,则有
,则有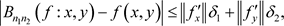

 ,可得
,可得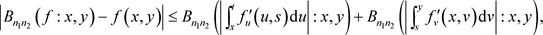
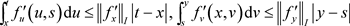

 ,则存在一个常数
,则存在一个常数 ,有下式成立:
,有下式成立:
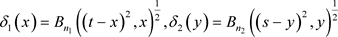 。
。 ,计算可得
,计算可得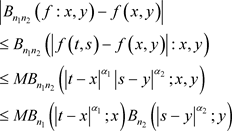
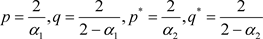
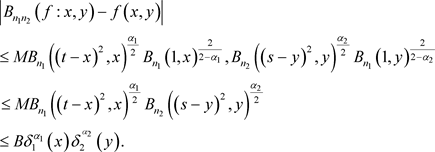
 即定理成立。
即定理成立。