Advances in Applied Mathematics
Vol.
09
No.
04
(
2020
), Article ID:
35285
,
10
pages
10.12677/AAM.2020.94069
The WENO Reconstruction Based on the Artificial Neural Network
Qi Liu1, Xiao Wen2
1School of Mathematical Sciences, Ocean University of China, Qingdao Shandong
2College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao Shandong

Received: Apr. 5th, 2020; accepted: Apr. 20th, 2020; published: Apr. 27th, 2020

ABSTRACT
A method for WENO reconstruction based on the artificial neural network (ANN) is proposed, which uses the ANN to approximate the non-linear weights in WENO-JS, where the input of the ANN is the value of the five-point function in the stencil for fifth-order WENO scheme, and the output is the smoothness indicators of the three sub-stencils. The smoothness indicators can be directly converted into corresponding non-linear weights for WENO reconstruction. Numerical experiments show that, compared with the WENO-JS scheme, the WENO-ANN can maintain accuracy, the numerical dispersion and dissipation are lower.
Keywords:Artificial Neural Network, WENO Scheme, Non-Linear Weights

基于人工神经网络的WENO重构方法
刘 琪1,温 晓2
1中国海洋大学数学科学学院,山东 青岛
2山东科技大学数学与系统科学学院,山东 青岛

收稿日期:2020年4月5日;录用日期:2020年4月20日;发布日期:2020年4月27日

摘 要
本文提出了一种基于人工神经网络(ANN)的WENO重构方法,用ANN来近似WENO-JS中的非线性权重,其中ANN的输入为用于五阶WENO求解的模板中的五点函数值,输出为三个子模板的光滑性指标,光滑性指标可直接转化为对应的非线性权重,用于WENO重构。数值实验表明,与WENO-JS相比,WENO-ANN能保持精度,且数值色散耗散较低。
关键词 :人工神经网络,WENO格式,非线性权重

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
对于流体力学中的某些初边界值问题(IBVP),在求解过程中,它们的数值解可能会在有限时间内形成不连续性,即冲击波。为了更好的处理这些不连续性,必须专门研究用于求解这类偏微分方程(PDE)的数值方法 [1]。
1987年,Harten等人 [2] 提出了一类称为本质无振荡(ENO)格式的高分辨率方法,该方法衡量了数值解在多个子模板上的光滑度,然后根据最光滑的子模板计算通量,以此来避免通过不连续性进行插值。1996年,Jiang和Shu等人 [3] 对ENO进行了改进,提出了加权本质无振荡方法(WENO-JS),该方法再次在多个子模板上计算光滑度。但是,WENO-JS不是仅采用最光滑的模板,而是采用每个模板上预测的通量的加权平均值来强调较平滑的模板。
之后的许多工作都是建立在原始的WENO-JS方法上,如修改光滑指示因子 [4] [5] [6],修改非线性权重 [7] [8] [9] 等。但是通过这类WENO-JS方法得到的数值解都会依赖于光滑指示因子和灵敏度参数,尽管现在已经有比较精确的光滑指示因子计算方法,但并没有研究表明,它们就是最优的选择。并且根据传统的光滑指示因子 [3] 得出的权重,在通量函数的一阶或高阶倒数消失的点上,无法恢复解的最高阶数 [7]。
在过去的几十年中,机器学习已在数据分析中变得无处不在,并且在求解PDE的数值解方面也得到了很多的重视。Lagaris等人 [10] 将微分方程解的形式参数化,用神经网络进行训练,并优化权重以减小解的残差。Yu等人 [11] 训练了一个神经网络来对局部光滑度进行分类,并根据此分类计算了人工粘度。Bar-Sinai等人 [12] 使用模拟数据将粗粒度模型嵌入到涉及神经网络的有限差分格式中,从而使它们可以在相对粗网格上实现低误差。Pfau等人 [13] 将特征值问题的特征函数参数化为神经网络,并将训练转化为双级优化问题以减少偏差,从而显著降低了内存需求。Hsieh等人 [14] 通过学习如何使用深度神经网络迭代地改进数值解,得到了特定领域的快速PDE求解器,与最先进的求解器 [15] 相比,其速度提高了2~3倍 [16]。
在本文中,我们构造了利用人工神经网络(ANN)求非线性权重的WENO方法(记为WENO-ANN)。其中ANN的输入为用于WENO求解的模板中的五点函数值,输出为三个子模板的光滑性指标, 光滑性指标可直接转化为对应的非线性权重,用于WENO重构。因此WENO-ANN在求解过程中不需要人工参数,提高了算法的稳定性。数值实验表明与WENO-JS相比,WENO-ANN能保持精度,且数值色散耗散较低。在高分辨率情况下,能有效提高计算效率。
2. 加权本质无振荡WENO-JS格式
满足双曲守恒律的可压缩流数值模型为
, (1)
考虑均匀网格点 ,公式(1)的离散格式可表示为
, (2)
其中 是点值 的数值近似。用于双曲守恒律的守恒有限差分公式要求在单元边界 处具有高阶一致的数值通量,以便在均匀分布的单元上形成通量差。可以通过隐式地定义
数值通量函数
来达到空间离散的守恒性质,从而使得(2)式中的空间导数可以在单元边界处通过守恒有限差分公式得到精确近似,
其中 。
处的高阶多项式插值可以通过已知网格点处的值 来计算。经典的五阶WENO格式如图1所示,
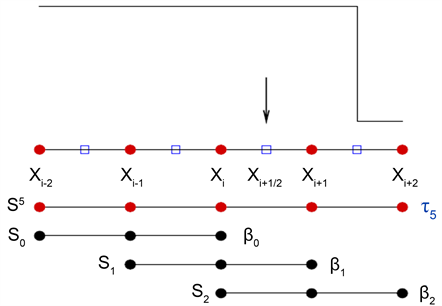
Figure 1. The model of the fifth-order WENO scheme
图1. 五阶WENO示意图
它把包含五个点的大模板 分成了三个子模板 ,其中每个子模板包含三个点。通过插值点值 的凸组合建立五阶多项式逼近 ,这里 是定义在每个子模板 上的三阶多项式,即单元边界 处的五阶WENO重构可表示为:
其中 为三个子模板上二次多项式 在 处的函数值:
五阶WENO-JS格式的非线性权重 为
其中灵敏度参数为 , 为理想权重且取值为 。 为光滑指示因子,用来
衡量子模板上的光滑性,可显式地写为
3. 基于BP神经网络的WENO权重算法
BP神经网络能学习和存储大量的输入–输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程,其网络模型拓扑结构包括输入层(input layer)、隐含层(hidden layer)和输出层(output layer)。BP神经网络的学习过程由前向计算过程和误差反向传播过程组成。在前向计算过程中,输入量从输入层经隐含层逐层计算,并传向输出层,每层神经元的状态只影响下一层神经元的状态。如果输出层不能得到期望的输出,则转入误差反向传播过程,误差信号沿原来的连接通路返回,逐次调整网络各层的权值和阈值,直至达到输入层,再重复向计算。这两个过程依次反复进行,不断调整各层的权重和阈值,使得网络误差最小或达到人们所期望的要求时,学习过程结束。
由公式(1)可知,计算每个单元边界 处的值时,都要重新计算非线性权重 ,并且在计算非线性权重时,会依赖于灵敏度参数和光滑指示因子的选择。因此我们考虑用BP神经网络来近似式(1)中的权重 ,从而避免人工参数的选择,输入 及其附近的函数值 ,可以快速的输出每个子模板上函数的光滑性,记为Index,然后将输出的光滑性指标Index转化为定每个子模板上的权重 ,两者的对应关系如表1所示。
Table 1. The corresponding relationship between the smoothness index and the weights of the sub-stencils ω k ( k = 0 , 1 , 2 )
表1. 光滑性指标Index与子模版上权重 的对应关系
3.1. 网络的输入输出
网络的输入为 及其附近的函数值 ,因此输入层神经元个数 。网络输出层神经元个数 ,为子模版光滑性指标Index,其与三个子模板的光滑性有关,具体见表2:
Table 2. The corresponding relationship between the smoothness index and the smoothness of the three sub-stencils S 0 , S 1 , S 2
表2. 三个子模板 上光滑性与子模版光滑性指标Index的对应关系
3.2. 数据集的设计
如3.1中所述,数据集的输入取函数 定义域D内某一点 及其左右两点处的函数值 ,函数 、参数取值、定义域、间断标识及每类函数的选取数量如表3所示。在神经网络训练过程中,随机选取80%进行训练,剩余的20%用于网络测试。
Table 3. The function f ( x ) , the value of the parameters, the domain, the smoothness index and the number of the functions in the data base
表3. 数据集中的函数 、参数取值、定义域、光滑性指标及训练集中每类函数的数量
3.3. 网络结构的确定
1) 网络的层数
1989年,Robert Hecht-Nielsen [17] 证明了对于任何闭区间内的一个连续函数,都可以用一个隐含层的BP网络来逼近,当学习不连续函数时BP网络需要两个隐含层。因此,本文选择两个隐含层 的BP网络。
2) 隐含层节点数
各隐藏层节点数的选取会影响神经网络的性能。若隐藏层中节点数太少,会出现网络识别未经训练样本能力差,容错性低等问题;若隐藏层节点数太多,则会导致网络学习时间大幅加长,样本中一些如干扰、噪声等非规律性内容存储进网络等问题。隐藏层的节点数往往与求解问题的要求,输入输出节点数有不可分割的联系。在本文中设置的隐含层节点数 。
3) 激活函数(activation function)
引入激活函数的目的是在模型中引入非线性。如果没有激活函数,那么无论神经网络有多少层,最终都是一个线性映射,单纯的线性映射无法解决线性不可分问题。
本文在隐含层 中均选用Relu激活函数( ),以增加特征效应;在输出层中选用
sigmoid激活函数( ),将输出数据映射到 的范围内,从而进行分类。
4) 数据的归一化处理。
对于大小不一致的输入函数值,本文中选取的S型激活函数(sigmoid)在输入数据过大时变化平缓,区分度太小。因此需要采取归一化算法对输入数据进行预处理,本文中采用线性归一化算法将数据归一化到 区间:
其中 是 的归一化向量。
综上所述,本文设计采用的间断点检测的BP神经网络模型为(图2):
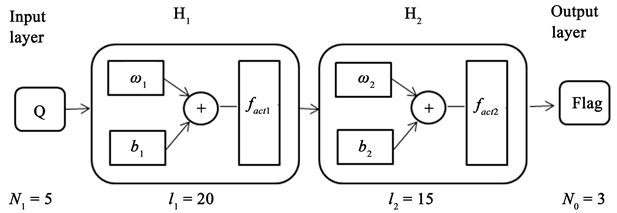
Figure 2. The model of the BP neural network
图2. BP神经网络模型
4. WENO-ANN格式
应用第二节中构造的人工神经网络,通过五个点的大模板 上的函数值计算非线性权重 ,并应用于WENO重构。算法如下:
算法1 WENO-ANN方法
1) 构建并训练神经网络,得出由五点函数值 计算三个子模板的光滑性指标Index的网络N。
2) 在计算过程中,对某一点 ,其左右两点处的函数值 作为网络输入,计算得出三个子模板的光滑性指标Index。
3) 根据表1,将神经网络输出的光滑性指标Index转化为非线性权重 ;
4) WENO重构: 。
5. 数值结果
在本节的数值实验中,PDEs离散后得到的关于时间的ODEs,使用了三阶TVD Runge-Kutta方法
其中,L是空间离散算子,CFL条件数为0.45。
5.1. 标量方程
本节首先考虑具有周期边界条件的波动方程
,其中初始条件考虑了光滑和间断两种情况:光滑初始条件为
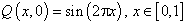 ,终止时间为
;间断初始条件为
,终止时间为
;间断初始条件为
终止时间 。
表4给出了在光滑初始条件下,WENO-ANN格式的 误差和 误差,可以看出WENO-ANN格式能保持五阶精度。
Table 4. The precision test of the wave equation with smooth initial condition
表4. 具有光滑初始条件的波动方程的精度测试
图3(左)展示了在间断初始条件下,WENO-ANN和WENO-JS格式所求得的数值解的比较,可以看出WENO-ANN格式具有相对较高的分辨率,数值耗散较低。
其次考虑具有周期边界条件的Burgers方程
其数值解如图3(右)所示,与WENO-JS格式相比具有同等精度。此外,表5给出了Burgers方程在两种格式下的CPU时间对比,可以看出,WENO-ANN格式在高分辨率下,会明显地提高计算效率。
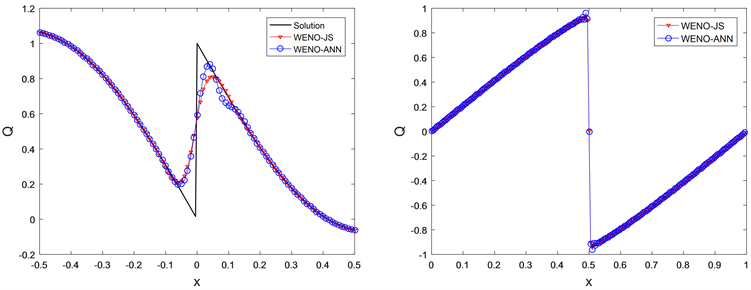
Figure 3. (Left) The numerical solution of the wave equation with the discotinuous initial condition, (Right) The numerical solution of the Burgers equation with
图3. (左) 具有间断初始条件的波动方程的数值解,(右) Burgers方程的数值解:网格节点数均为
Table 5. The comparison of the CPU time for Burgers equation
表5. Burgers方程的CPU时间对比
5.2. 一维欧拉方程
在本节中,考虑强守恒形式的一维欧拉方程
其中,
状态方程 , 分别是密度,速度,压力和总能量。
下面将对一维欧拉方程中的典型问题Sod问题、Lax问题、Shock-Density问题以及Shock-Entropy问题进行数值实验,来验证所提方法的准确性和有效性。
Sod问题的初始条件为
终止时间 ,网格节点数 。
Lax问题的初始条件为
终止时间 ,网格节点数 。
Shock-Density问题的初始条件为
其中, ,终止时间 ,网格节点数 。
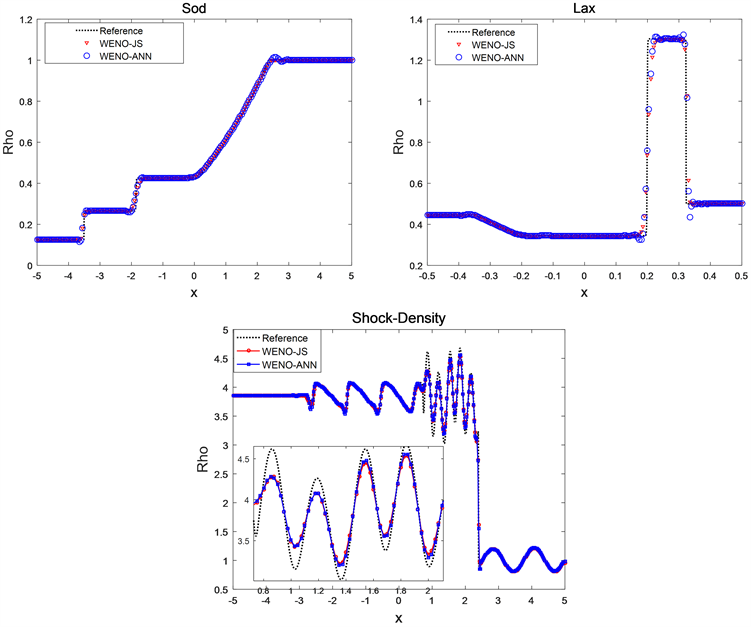
Figure 4. The solutions of the density for the Sod problem, the Lax problem and the Shock-Density problem
图4. Sod问题、Lax问题和Shock-Density问题的密度解
图中Sod问题、Lax问题和Shock-Density问题的参考解是五阶WENO-JS格式在网格节点数 下的数值解。如图4所示,WENO-ANN格式能很好的捕捉间断结构,且与WENO-JS格式相比,WENO-ANN格式的数值耗散更小,具有更高的精度。
6. 结论
本文在五阶WENO-JS的基础上,用人工神经网络(ANN)代替传统的非线性权重计算方法,将用于五阶WENO求解的模板中的五点函数值作为ANN的输入,三个子模板的光滑性指标作为输出,光滑性指标可直接转化为对应的非线性权重,用于WENO重构。数值实验表明,该网络能很好的捕捉间断,与WENO-JS相比,WENO-ANN能保持精度,且数值色散耗散较低,在高分辨率下,能有效提高计算效率。
文章引用
刘 琪,温 晓. 基于人工神经网络的WENO重构方法
The WENO Reconstruction Based on the Artificial Neural Network[J]. 应用数学进展, 2020, 09(04): 574-583. https://doi.org/10.12677/AAM.2020.94069
参考文献
- 1. LeVeque, R.J. (2002) Finite Volume Methods for Hyperbolic Problems. Cambridge University Press, Cambridge, 31. https://doi.org/10.1017/CBO9780511791253
- 2. Harten, A., Engquist, B., Osher, S. and Chakravarthy, S.R. (1987) Uniformly High Order Accurate Essentially Non-Oscillatory Schemes, III. In: Upwind and High-Resolution Schemes, Springer, Berlin, 231-303. https://doi.org/10.1007/978-3-642-60543-7_12
- 3. Jiang, G. and Shu, C.-W. (1996) Efficient Implementation of Weighted Eno Schemes. Journal of Computational Physics, 126, 202-228. https://doi.org/10.1006/jcph.1996.0130
- 4. Ha, Y., Kim, C., Lee, Y. and Yoon, J. (2013) An Improved Weighted Essentially Non-Oscillatory Scheme with a New Smoothness Indicator. Journal of Computational Physics, 232, 68-86. https://doi.org/10.1016/j.jcp.2012.06.016
- 5. Kim, C., Ha, Y. and Yoon, J. (2016) Modified Non-Linear Weights for Fifth-Order Weighted Essentially Non-Oscillatory Schemes. Journal of Computational Physics, 67, 299-323. https://doi.org/10.1007/s10915-015-0079-3
- 6. Rathan, S. and Raju, G. (2018b) A Modified Fifth-Order WENO Scheme for Hyperbolic Conservation Laws. Computers & Mathematics with Applications, 75, 1531-1549. https://doi.org/10.1016/j.camwa.2017.11.020
- 7. Borges, R., Carmona, M., Costa, B. and Don, W.S. (2008) An Improved Weighted Essentially Non-Oscillatory Scheme for Hyperbolic Conservation Laws. Journal of Computational Physics, 227, 3191-3211. https://doi.org/10.1016/j.jcp.2007.11.038
- 8. Castro, M., Costa, B. and Don, W.S. (2011) High Order Weighted Essentially Non-Oscillatory Weno-Z Schemes for Hyperbolic Conservation Laws. Journal of Computational Physics, 230, 1766-1792. https://doi.org/10.1016/j.jcp.2010.11.028
- 9. Rathan, S. and Raju, G. (2018) Improved Weighted Eno Scheme Based on Parameters Involved in Nonlinear Weights. Applied Mathematics and Computation, 331, 120-129. https://doi.org/10.1016/j.amc.2018.03.034
- 10. Lagaris, I., Likas, A. and Fotiadis, D. (1998) Artificial Neural Networks for Solving Ordinary and Partial Differential Equations. IEEE Transactions on Neural Networks, 9, 987-1000. https://doi.org/10.1109/72.712178
- 11. Yu, J., Hesthaven, J.S. and Yan, C. (2018) A Data-Driven Shock Capturing Approach for Discontinuous Galerkin Methods. Technical Report.
- 12. Bar-Sinai, Y., Hoyer, S., Hickey, J. and Brenner, M. (2019) Learning Data-Driven Discretizations for Partial Differential Equations. PNAS, 116, 15344-15349. https://doi.org/10.1073/pnas.1814058116
- 13. Pfau, D., Petersen, S., Agarwal, A., Barrett, D.G.T. and Stachenfeld, K.L. (2018) Spectral Inference Networks: Unifying Deep and Spectral Learning.
- 14. Hsieh, J.T., Zhao, S.J., Eismann, S., Mirabella, L. and Ermon, S. (2019) Learning Neural PDE Solvers with Convergence Guaran-tees.
- 15. Logg, A., Mardal, K.A. and Wells, G. (2012) Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book. Springer, Berlin. https://doi.org/10.1007/978-3-642-23099-8
- 16. Stevens, B. and Colonius, T. (2020) Enhancement of Shock-Capturing Methods via Machine Learning.
- 17. Hecht-Nielsen, R. (1988) Theory of the Back-Propagation Neural Network. Neural Networks, 1, 445. https://doi.org/10.1016/0893-6080(88)90469-8
