ABSTRACT

Stochastic interest rate is an important issue in the research of actuarial science. The basic theory of probability statistics, financial mathematics and stochastic processes is used to establish the double stochastic model consisting of Brownian motion and Poisson process for the interest force function. The actuarial present value of death insurance and survival annuities for individual and four-unit joint life insurance models is derived, and specific expressions for fully discrete annual equilibrium net premium and net liability reserve are given. For four-unit joint life insurance, we mainly study the actuarial theory in the joint survival state and the last survivor state. The conclusions obtained have a high application value for the development and design of life insurance products.

Keywords:Stochastic Interest, Double-Stochastic Model, Fully Discrete Insurance, Life Insurance Actuarial Model

随机利率下完全离散险种的寿险精算模型

吕嘉全

曲阜师范大学统计学院，山东 曲阜

收稿日期：2020年6月7日；录用日期：2020年6月22日；发布日期：2020年6月28日

摘 要

随机利率是寿险精算学研究的重要问题。本文利用概率统计、金融数学、随机过程的基本理论对利息力函数建立由反射布朗运动和泊松过程组成的双随机模型，推导出个人和四元联合寿险模型的死亡保险和生存年金的精算现值，并给出完全离散险种的年均衡净保费和净责任准备金的具体表达式。对于四元联合寿险保单，本文主要研究在联合生存状态和最后生存者状态下的精算理论。所得到的结论对寿险产品的开发与设计具有较高的应用价值。

关键词 :随机利率，双随机模型，完全离散险种，寿险精算模型

Copyright © 2020 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

保险业在国民经济中具有举足轻重的作用。习近平总书记在报告中提出，“十三五”时期是我国全面建设小康社会的决定性阶段，也是由保险大国向保险强国转变的关键时期。2019年全国保费收入42,645亿元占国内生产总值的4.3%，较2018年增长12.17%，较2015年增长75.6%，但远低于世界平均水平。近年来，寿险缴纳的保费占保费总收入的比例高于50%。由此可见：我国寿险具有广阔的市场前景。2019年全国银行系统会议指出，我国利率市场化改革正稳步进行。利率的细微波动对寿险产品的定价有着重要的影响，所以我们基于随机利率下来探讨寿险精算模型。另外，随着“二孩政策”的全面实施，一家四口的社会状况逐渐增多，故对于四元联合寿险的研究显得尤为重要。

最初学者为使计算简单，在固定利率的假设下对寿险精算理论进行了研究，现在此类成果十分丰富。1971年，Pollard J. H. [1] 首次在精算模型研究中将利率视为随机变量。随后，学者们开始对利息力或利息力累积函数建立随机模型。2008年，程海兵 [2] 对利率建立由反射布朗运动和负二项分布组成的双随机模型，研究了全连续型变额寿险精算模型中的相关理论。2008年，郭春增 [3] 建立由维纳过程和负二项分布组成的双随机利率模型，推导出半连续型寿险精算模型中的相关表达式。2009年，贾念念 [4] 对利息力累积函数建立了由高斯过程与泊松过程组成的双随机模型，研究了半连续型变额寿险保单中的相关精算理论。2013年，郭欣 [5] 选取正态分布和布朗运动对利息力函数分别进行建模，推导出完全离散型险种的均衡净保费以及责任准备金的表达式。

2006年，东明 [6] 研究了随机利率下的联合寿险模型，给出了精算现值和与其相对应方差的表达式。2012年，纪艳辉 [7] 对利息力积累函数建立由负二项分布和维纳过程组成的双随机模型，研究了服从Weibull死亡力假设的二元寿险模型，推导出半连续型年缴纯保费和责任准备金的具体表达式。2016年，钟远威 [8] 在固定利率的前提下，研究了三元寿险精算模型，分别给出连续型和离散型险种的趸交净保费和年金精算现值的公式，并且选取“布朗运动 + 常见分布”建立随机利率模型，推导出联合生存状态和最后生存状态下的趸交纯保费和年金现值的具体表达式。2018年，张潇月 [9] 选取反射布朗运动和泊松过程对利息力函数建立随机模型，讨论了四元寿险模型中的精算现值，给出了连续型均衡纯保费的具体表达式。

通过阅读文献发现：学者对于完全离散型险种的研究还比较少；家庭联合寿险模型的研究多限于夫妻联合寿险模型和三元家庭联合寿险模型，有关四元家庭联合寿险的研究还不是特别多。鉴于此，本文选取目前最具有广泛性的反射布朗运动和泊松过程建立随机利率模型，在此基础上讨论完全离散型险种的寿险精算模型，即以期初付生存年金的方式缴纳保费并且在被保险人的死亡年度末给付保险金。此类保单更符合现实情况，有较强的实用价值。

2. 预备知识

2.1. 生存模型

2.1.1. 一元生存模型

我们用(x)表示x岁的个体， $T\left(x\right)$ 表示(x)未来生存的时间， $K\left(x\right)$ 表示(x)未来生存时间的整数年。 定义 $F_{T\left(x\right)}\left(t\right)$ 为 $T\left(x\right)$ 的分布函数，即

$F_{T\left(x\right)}\left(t\right)=P\left[T\left(x\right)\le t\right].$ (2-1)

显然，它表示x岁的个体在未来t年内死亡的概率。在精算学中，我们用 ${}_{t}q{}_x$ 来表示。 特别地， ${}_{t|u}q{}_x$ 表示(x)活过 $x+u$ 岁但在 $x+u+t$ 岁之前死亡的概率，即

${}_{u|t}q{}_x={}_{u}p{}_x-{}_{u+t}p{}_x={}_{u}p{}_x{}_{t}q{}_{x+u}.$ (2-2)

与之对应的为生存函数 $s_{T\left(x\right)}\left(t\right)$，即

$s_{T\left(x\right)}\left(t\right)=1-F_{T\left(x\right)}\left(t\right)=1-P\left[T\left(x\right)\le t\right]=P\left[T\left(x\right)>t\right].$ (2-3)

在精算学中，它表示(x)活过 $x+t$ 岁的概率，记作 ${}_{t}p{}_x$。

2.1.2. 四元生存模型

我们先引入两个基本概念：由(x)，(y)，(w)，(z)组成的四元联合生存状态和最后生存者状态，分别用 $\left(xywz\right)$ 和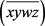来表示。所谓联合生存状态，就是指四元联合保单中的每个个体都存在时的状态。最后生存者状态是指四元联合保单中至少有一个个体存在时的状态。显然，最后生存者状态包含联合生存状态。本文关于联合保单的讨论，均假设个体之间是相互独立的，也就是说个体之间是不相关的。记由(x)，(y)，(w)，(z)组成的四元联合体为M。

我们用 $T\left(xywz\right)$ 表示 $\left(xywz\right)$ 未来生存的时间， $K\left(xywz\right)$ 表示 $\left(xywz\right)$ 未来生存时间的整数年。根据定义，容易写出

$T\left(xywz\right)=\min \left\{T\left(x\right),T\left(y\right),T\left(w\right),T\left(z\right)\right\}.$

定义 $T\left(xywz\right)$ 的生存函数为 $s_{T\left(xywz\right)}\left(t\right)$，即

$\begin{array}{c}{s}_{T\left(xywz\right)}\left(t\right)=P\left[T\left(xywz>t\right)\right]\\ =P\left[\min \left\{T\left(x\right),T\left(y\right),T\left(w\right),T\left(z\right)\right\}>t\right]\\ =P\left[T\left(x\right)>t,T\left(y\right)>t,T\left(w\right)>t,T\left(z\right)>t\right]\\ =P\left[T\left(x\right)>t\right]P\left[T\left(y\right)>t\right]P\left[T\left(w\right)>t\right]P\left[T\left(z\right)>t\right]\\ ={}_{t}p{}_x{}_{t}p{}_y{}_{t}p{}_w{}_{t}p{}_z.\end{array}$ (2-4)

在精算学中，它表示 $\left(xywz\right)$ 未来时刻t仍存在的概率，记作 ${}_{t}p{}_{xywz}$。与生存概率 ${}_{t}p{}_{xywz}$ 对应的是死亡概率 ${}_{t}q{}_{xywz}$，它表示 $\left(xywz\right)$ 在未来t年内终止的概率，即 $T\left(xywz\right)$ 的分布函数 $F_{T\left(xywz\right)}(\; t\; )$

$\begin{array}{c}{F}_{T\left(xywz\right)}\left(t\right)=P\left[T\left(xywz\right)\le t\right]\\ =1-P\left[T\left(xywz\right)>t\right]\\ =1-{}_{t}p{}_x{}_{t}p{}_y{}_{t}p{}_w{}_{t}p{}_z.\end{array}$ (2-5)

我们考虑 $K\left(xywz\right)$ 的概率函数，即

$\begin{array}{c}P\left[K\left(xywz\right)=j\right]=P\left[j\le K\left(xywz\right)<j+1\right]\\ =P\left[j\le T\left(xywz\right)<j+1\right]\\ ={}_{j|}q{}_{xywz}\\ ={}_{j}p{}_{xywz}{q}_{x+j:y+j:w+j:z+j},j=1,2,3,\cdots \end{array}$ (2-6)

同样地，我们用 $T\left(\overline{xywz}\right)$ 表示 $\left(\overline{xywz}\right)$ 未来生存的时间， $K\left(\overline{xywz}\right)$ 表示 $\left(\overline{xywz}\right)$ 未来生存时间的整数年。 根据定义，显然有下面等式成立

$T\left(\overline{xywz}\right)=\max \left\{T\left(x\right),T\left(y\right),T\left(w\right),T\left(z\right)\right\}.$

我们定义 $T\left(\overline{xywz}\right)$ 的分布函数为 $F_{T\left(\overline{xywz}\right)}\left(t\right)$，即

$\begin{array}{c}{F}_{T\left(\overline{xywz}\right)}\left(t\right)=P\left[T\left(\overline{xywz}\right)\le t\right]\\ =P\left[\max \left\{T\left(x\right),T\left(y\right),T\left(w\right),T\left(z\right)\right\}\le t\right]\\ =P\left[T\left(x\right)\le t\right]P\left[T\left(y\right)\le t\right]P\left[T\left(w\right)\le t\right]P\left[T\left(z\right)\le t\right]\\ ={}_{t}q{}_x{}_{t}q{}_y{}_{t}q{}_w{}_{t}q{}_z=\left(1-{}_{t}p{}_x\right)\left(1-{}_{t}p{}_y\right)\left(1-{}_{t}p{}_w\right)\left(1-{}_{t}p{}_z\right).\end{array}$ (2-7)

在精算学中，它表示 $\left(\overline{xywz}\right)$ 在未来t年内终止的概率，记作 ${}_{t}q{}_{\overline{xywz}}$。与分布函数 $F_{T\left(\overline{xywz}\right)}\left(t\right)$ 对应的是生存函数 $s_{T\left(\overline{xywz}\right)}\left(t\right)$，即

$\begin{array}{c}{s}_{T\left(\overline{xywz}\right)}\left(t\right)=P\left[T\left(\overline{xywz}\right)>t\right]=1-P\left[T\left(\overline{xywz}\right)\le t\right]\\ =1-P\left[\max \left\{T\left(x\right),T\left(y\right),T\left(w\right),T\left(z\right)\right\}\le t\right]\\ =1-P\left[T\left(x\right)\le t\right]P\left[T\left(y\right)\le t\right]P\left[T\left(w\right)\le t\right]P\left[T\left(z\right)\le t\right]\\ =1-\left(1-{}_{t}p{}_x\right)\left(1-{}_{t}p{}_y\right)\left(1-{}_{t}p{}_w\right)\left(1-{}_{t}p{}_z\right)\\ =1-{}_{t}q{}_x{}_{t}q{}_y{}_{t}q{}_w{}_{t}q{}_z.\end{array}$ (2-8)

显然，它表示 $\left(\overline{xywz}\right)$ 在未来时刻t仍存在的概率，用精算符号记作 ${}_{t}p{}_{\overline{xywz}}$。接下来，我们考察 $K\left(\overline{xywz}\right)$ 的概率密度函数

$\begin{array}{c}P\left[K\left(\overline{xywz}\right)=j\right]=P\left[T\left(\overline{xywz}\right)<j+1\right]-P\left[T\left(\overline{xywz}\right)<j\right]\\ ={}_{j+1}q{}_{\overline{xywz}}-{}_{j}q{}_{\overline{xywz}}\\ ={}_{j+1}q{}_x{}_{j+1}q{}_y{}_{j+1}q{}_w{}_{j+1}q{}_z-{}_{j}q{}_x{}_{j}q{}_y{}_{j}q{}_w{}_{j}q{}_z.\end{array}$ (2-9)

2.2. 模型构建

2.2.1. 反射布朗运动

定义2.1 [10] 若一个随机过程 $\left\{B\left(t\right),t\ge 0\right\}$ 满足：

1) $B\left(t\right)$ 是独立增量过程；

2) $\forall s,t>0$，$B\left(s+t\right)-B\left(s\right)~N\left(0,t\right)$，即 $B\left(s+t\right)-B\left(s\right)$ 是期望为0，方差t的正态分布；

3) $B\left(t\right)$ 是关于t的连续函数。

那么称 $\left\{B\left(t\right),t\ge 0\right\}$ 为标准布朗运动。它在t时刻的密度函数为

$f_t\left(x\right)=\frac{1}{\sqrt{2\pi t}}{\text{e}}^{-\frac{x^2}{2t}}.$ (2-10)

若 $G\left(t\right)=\left|B\left(t\right)\right|$，则称 $G\left(t\right)$ 为反射布朗运动。

性质2.1 若 $\left\{B\left(t\right),t\ge 0\right\}$ 为标准布朗运动，则 $E\left[{\text{e}}^{-\alpha \left|B\left(t\right)\right|}\right]=2{\text{e}}^{\frac{{\alpha }^{2}t}{2}}\left[1-\Phi \left(\alpha \sqrt{t}\right)\right]$。

2.2.2. 泊松过程

定义2.2 [11] 若一个随机过程 $\left\{N\left(t\right),t\ge 0\right\}$ 满足：

1) $N\left(t\right)=0$ ；

2) $\left\{N\left(t\right),t\ge 0\right\}$ 过程有平稳增量和独立增量；

3) $P\left\{N\left(t+h\right)-N\left(t\right)=1\right\}=\lambda h+o\left(h\right)$ ；

4) $P\left\{N\left(t+h\right)-N\left(t\right)\ge 2\right\}=o\left(h\right)$。

那么称 $\left\{N\left(t\right),t\ge 0\right\}$ 为具有速率 $\lambda \left(\lambda >0\right)$ 的泊松过程。

性质2.2 [11] 若 $\left\{N\left(t\right),t\ge 0\right\}$ 是具有速率 $\lambda \left(\lambda >0\right)$ 的泊松过程，则对一切 $s>0$，$t>0$，$N\left(s+t\right)-N\left(s\right)$ 是均值 $\lambda t$ 的泊松随机变量。即

$P\left[N\left(s+t\right)-N\left(s\right)=k\right]={\text{e}}^{-\lambda t}\frac{{\left(\lambda t\right)}^k}{k!}.$ (2-11)

性质2.3 若 $\left\{N\left(t\right),t\ge 0\right\}$ 是具有速率 $\lambda \left(\lambda >0\right)$ 的泊松过程，则 $\left[{\text{e}}^{-\beta N\left(t\right)}\right]={\text{e}}^{\lambda t\left({\text{e}}^{-\beta }-1\right)}$。

2.2.3. 利息力函数模型

通常情况下利率总是围绕均值上下波动并且是非负的，反射布朗运动恰好具有这样良好的性质可以描述此类过程。泊松过程是一类计数过程，可以很好的描述突发事件对利率的影响。基于此，我们选用反射布朗运动和泊松过程对利息力函数建立双随机模型。设利息力函数为

$\delta \left(t\right)=\delta t+\alpha \left|B\left(t\right)\right|+\beta N(\; t\; )$

其中，假设B(t)与N(t)是相互独立的。则贴现函数为

$v\left(t\right)={\text{e}}^{-\delta \left(t\right)}={\text{e}}^{-\left[\delta t+\alpha \left|B\left(t\right)\right|+\beta N\left(t\right)\right]}.$

3. 一元寿险精算模型

3.1. 精算现值理论

这一节我们主要讨论寿险模型中的精算现值理论。我们先明确两个基本概念：现值和精算现值。 现值是指未来资金在现在的价值。 所谓精算现值指的是未来给付额对现在贴现值的期望，也就是现值的期望。下面我们分别介绍死亡保险和生存年金的精算现值。

3.1.1. 死亡保单年度末给付的死亡保险

死亡保险是以被保险人的死亡作为给付标的的险种，若被保险人在签单有效期内死亡，则保险人按照保险合同给付保险金，否则不予给付。

对于x岁的个体购买保险金为1的终身死亡保险，假设被保险人(x)的死亡时刻为 $T\left(x\right)$，则保险金给付的时刻为 $K\left(x\right)+1$。那么它的现值可以表示为

$Z=v^{K\left(x\right)+1}.$

我们记Z的精算现值为A_x

$\begin{array}{c}{A}_x=E\left[{\text{e}}^{-\delta \left(t\right)}\right]=E_B{E}_N{E}_T\left[{\text{e}}^{-\delta \left(t\right)}\right]\\ =E_B{E}_N\left[{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{}_{j}p{}_x}{q}_{x+j}\right]\\ ={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-{\text{e}}^{-\delta \left(j+1\right)}}{E}_B\left[{\text{e}}^{-\alpha \left|B\left(j+1\right)\right|}\right]E_N\left[{\text{e}}^{-\beta N\left(j+1\right)}\right]}{}_{j}p{}_x{q}_{x+j}\\ =2{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_x{q}_{x+j}.\end{array}$ (3-1)

3.1.2. 期初领取的生存年金

生存年金是以年金领取人的生存作为给付标的的险种，若领取人(x)在合同期限内的每年年初还生存，则领取1单位的生存年金，否则不予给付。

对于终身生存年金，假设领取人(x)的死亡时刻为 $T\left(x\right)$，则领取年金的时间长度为 $K\left(x\right)+1$。我们用

${\ddot{a}}_{\overline{K\left(x\right)+1\hspace{.2em}|}}$ 来表示它的现值，即

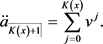
其精算现值我们记为 ${\ddot{a}}_x$

$\begin{array}{c}{\ddot{a}}_x=E\left[{\ddot{a}}_{\overline{K\left(x\right)+1\hspace{.2em}|}}\right]=E_B{E}_N{E}_T\left[{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j\right)}}{I}_{\left\{K\left(x\right)\ge j\right\}}\right]\\ ={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{E}_B\left[{\text{e}}^{-\alpha \left|B\left(j\right)\right|}\right]E_N\left[{\text{e}}^{-\beta N\left(j\right)}\right]}{}_{j}p{}_x\\ =2{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{\text{e}}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_x.\end{array}$ (3-2)

3.2. 完全离散险种的年均衡净保费

对于一个完整的寿险精算模型，我们还需要考虑保费的缴纳方式。通常情况下，保费缴纳分为趸缴净保费和分期缴纳保费。所谓趸缴就是指在签单时一次性缴完保费。分期缴纳保费就是把保费分成若干个时期进行缴纳，最常见的形式是以年均衡净保费的方式缴纳。本文主要讨论完全离散险种的年均衡净保费问题，即以期初付生存年金的方式缴纳保费并且在被保险人的死亡年度末给付保险金。

保费的厘定需满足平衡准则 [12]：缴纳保费的精算现值等于保险金给付的精算现值。由平衡准则我们可知：趸缴净保费在数值上等于死亡保险的精算现值，所以本文不再讨论趸缴净保费。我们考虑此类保单：x岁的个体购买单位保额的完全离散型终身死亡保险。假设被保险人的死亡时刻为 $T\left(x\right)$，则停止缴

费的时刻为 $K\left(x\right)+1$ 那么保费缴纳的现值可以表示为 $P_x{\ddot{a}}_{\overline{K\left(x\right)+1\hspace{.2em}|}}$，保险金给付的现值记为 $v^{K\left(x\right)+1}$。故保单损

失量可以表示为

$L=v^{K\left(x\right)+1}-P_x{\ddot{a}}_{\overline{K\left(x\right)+1\hspace{.2em}|}}.$

利用平衡准则可以推出

$A_x-P_x{\ddot{a}}_x=0.$

所以年均衡净保费为

$P_x=\frac{A_x}{{\ddot{a}}_x}=\frac{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_x{q}_{x+j}}{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{e}^{-\delta j}{e}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_x}.$ (3-3)

3.3. 完全离散险种的净责任准备金

我们在上一节探讨了基于完全离散险种的年均衡净保费问题，在此基础上，这一节我们讨论完全离散险种的净责任准备金。净责任准备金 [12] 是保险人为了能够应对未来有效保单的索赔，提前准备的一些资金。通常情况下计算准备金的方法有两种：过去法和未来法。过去法是根据保险人过去的收支差额来计算准备金，未来法是根据保险人未来的收支差额来计算准备金。

我们考虑此类保单：年龄为x岁的个体购买保额为1的完全离散型终身死亡保险，保费以年均衡净保费的形式缴纳。则在第t个保单年度末的未来损失量可以表示为

${}_{t}L{}_x=\left(v^{K\left(x\right)-t+1}-P_x{\ddot{a}}_{\overline{K\left(x\right)-t+1\hspace{.2em}|}}\right)I_{\left\{K\left(x\right)\ge t\right\}}.$

我们记它的净责任准备金为 ${}_{t}V{}_x$，利用未来法可以推出

$\begin{array}{c}{}_{t}V{}_x=A_{x+t}-P_x{\ddot{a}}_{x+t}\\ =2{\displaystyle \underset{j=\text{0}}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{x+t}{q}_{x+t+j}\\ -2\frac{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_x{q}_{x+j}}{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{e}^{-\delta j}{e}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_x}\\ \times {\displaystyle \underset{j=\text{0}}{\overset{\infty }{\sum }}{e}^{-\delta j}{e}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{x+t}.\end{array}$ (3-4)

4. 四元联合寿险精算模型

本章是第三章的推广，即在随机利率下由一元寿险精算模型向四元联合寿险精算模型的推广。 这一章我们主要讨论四元联合生存状态和最后生存者状态下的有关问题。

4.1. 死亡保单年度末给付的死亡保险

对于联合体M购买保险金为1的终身死亡保险。在联合生存状态下，假设 $\left(xywz\right)$ 的终止时刻为 $T\left(xywz\right)$，则保险金给付的时刻为 $K\left(xywz\right)+1$。那么它的精算现值为

$\begin{array}{c}{A}_{xywz}=E\left[{\text{e}}^{-\delta \left(t\right)}\right]=E_B{E}_N{E}_T\left[{\text{e}}^{-\delta \left(t\right)}\right]\\ =E_B{E}_N\left[{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{}_{j}p{}_{xywz}}{q}_{x+j:y+j:w+j:z+j}\right]\\ ={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{E}_B\left[{\text{e}}^{-\alpha \left|B\left(j+1\right)\right|}\right]E_N\left[{\text{e}}^{-\beta N\left(j+1\right)}\right]}{}_{j}p{}_{xywz}{q}_{x+j:y+j:w+j:z+j}\\ =2{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{xywz}{q}_{x+j:y+j:w+j:z+j}.\end{array}$ (4-1)

在最后生存者状态下，假设 $\left(\overline{xywz}\right)$ 的终止时刻为 $T\left(\overline{xywz}\right)$，则保险金给付的时刻为 $K\left(\overline{xywz}\right)+1$。那么它的精算现值为

$\begin{array}{c}{A}_{\overline{xywz}}=E\left[{\text{e}}^{-\delta \left(t\right)}\right]=E_B{E}_N{E}_T\left[{\text{e}}^{-\delta \left(t\right)}\right]\\ =E_B{E}_N\left[{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}\left({}_{j+1}q{}_{\overline{xywz}}-{}_{j}q{}_{\overline{xywz}}\right)}\right]\\ ={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{E}_B\left[{\text{e}}^{-\alpha \left|B\left(j+1\right)\right|}\right]E_N\left[{\text{e}}^{-\beta N\left(j+1\right)}\right]}\left({}_{j+1}q{}_{\overline{xywz}}-{}_{j}q{}_{\overline{xywz}}\right)\\ =2{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}\left({}_{j+1}q{}_{\overline{xywz}}-{}_{j}q{}_{\overline{xywz}}\right).\end{array}$ (4-2)

4.2. 期初领取的生存年金

对于联合体M参加单位保额的终身生存年金。在联合生存状态下，假设 $\left(xywz\right)$ 的终止时刻为 $T\left(xywz\right)$，则年金领取的时间长度为 $K\left(xywz\right)+1$。那么它的精算现值为

$\begin{array}{c}{\ddot{a}}_{xywz}=E\left[{\ddot{a}}_{\overline{K\left(xywz\right)+1\hspace{.2em}|}}\right]\\ =E_B{E}_N{E}_T\left[{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j\right)}}{I}_{\left\{K\left(xywz\right)\ge j\right\}}\right]\\ ={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{E}_B\left[{\text{e}}^{-\alpha \left|B\left(j\right)\right|}\right]E_N\left[{\text{e}}^{-\beta N\left(j\right)}\right]}{}_{j}p{}_{xywz}\\ =2{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{\text{e}}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{xywz}.\end{array}$ (4-3)

在最后生存者状态下，假设 $\left(\overline{xywz}\right)$ 的终止时刻为 $T\left(\overline{xywz}\right)$，则年金领取的时间长度为 $K\left(\overline{xywz}\right)+1$ 那么它的精算现值为

$\begin{array}{c}{\ddot{a}}_{\overline{xywz}}=E\left[{\ddot{a}}_{\overline{K\left(\overline{xywz}\right)+1\hspace{.2em}|}}\right]\\ =E_B{E}_N{E}_T\left[{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j\right)}}{I}_{\left\{K\left(\overline{xywz}\right)\ge j\right\}}\right]\\ ={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{E}_B\left[{\text{e}}^{-\alpha \left|B\left(j\right)\right|}\right]E_N\left[{\text{e}}^{-\beta N\left(j\right)}\right]}{}_{j}p{}_{\overline{xywz}}\\ =2{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{\text{e}}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{\overline{xywz}}.\end{array}$ (4-4)

4.3. 完全离散险种的年均衡净保费

对于联合体M购买保险金为1的完全离散型终身死亡保险。 在联合生存状态下，假设 $\left(xywz\right)$ 的终止时刻为 $T\left(xywz\right)$，那么根据(4-1)、(4-3)可得它的年均衡净保费

$P_{xywz}=\frac{A_{xywz}}{{\ddot{a}}_{xywz}}=\frac{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{xywz}{q}_{x+j:y+j:w+j:z+j}}{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{\text{e}}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{xywz}}.$ (4-5)

在最后生存者状态下，假设 $\left(\overline{xywz}\right)$ 的终止时刻为 $T\left(\overline{xywz}\right)$，那么根据(4-2)、(4-4)可得它的年均衡净保费

$P_{\overline{xywz}}=\frac{A_{\overline{xywz}}}{{\ddot{a}}_{\overline{xywz}}}=\frac{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}\left({}_{j+1}q{}_{\overline{xywz}}-{}_{j}q{}_{\overline{xywz}}\right)}{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{\text{e}}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{\overline{xywz}}}.$ (4-6)

4.4. 完全离散险种的净责任准备金

对于联合体M购买保险金为1的完全离散型终身死亡保险。在联合生存状态下，假设 $\left(xywz\right)$ 的终止时刻为 $T\left(xywz\right)$，那么根据(4-1)、(4-3)、(4-5)可得它的净责任准备金

$\begin{array}{c}{}_{t}V{}_{xywz}=A_{x+t:y+t:w+t:z+t}-P_{xywz}{\ddot{a}}_{x+t:y+t:w+t:z+t}\\ =2{\displaystyle \underset{j=\text{0}}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{x+t:y+t:w+t:z+t}{q}_{x+t+j:y+t+j:w+t+j:z+t+j}\\ -\frac{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{xywz}{q}_{x+j:y+j:w+j:z+j}}{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{\text{e}}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{xywz}}\\ \times 2{\displaystyle \underset{j=\text{0}}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{\text{e}}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{x+t:y+t:w+t:z+t}.\end{array}$ (4-7)

在最后生存者状态下，假设 $\left(\overline{xywz}\right)$ 的终止时刻为 $T\left(\overline{xywz}\right)$，那么根据(4-2)、(4-4)、(4-6)可得它的年均衡净保费

$\begin{array}{c}{}_{t}V{}_{\overline{xywz}}=A_{\overline{xywz}+t}-P_{\overline{xywz}}{\ddot{a}}_{\overline{xywz}+t}\\ =2{\displaystyle \underset{j=\text{0}}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}\left({}_{j+1}q{}_{\overline{xywz}+t}-{}_{j}q{}_{\overline{xywz}+t}\right)\\ -\frac{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta \left(j+1\right)}{\text{e}}^{\frac{1}{2}{\alpha }^2\left(j+1\right)}\left[1-\Phi \left(\alpha \sqrt{j+1}\right)\right]{\text{e}}^{\lambda \left(j+1\right)\left({\text{e}}^{-\beta }-1\right)}}\left({}_{j+1}q{}_{\overline{xywz}+t}-{}_{j}q{}_{\overline{xywz}+t}\right)}{{\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{\text{e}}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{\overline{xywz}}}\\ \times 2{\displaystyle \underset{j=\text{0}}{\overset{\infty }{\sum }}{\text{e}}^{-\delta j}{\text{e}}^{\frac{1}{2}{\alpha }^{2}j}\left[1-\Phi \left(\alpha \sqrt{j}\right)\right]{\text{e}}^{\lambda j\left({\text{e}}^{-\beta }-1\right)}}{}_{j}p{}_{\overline{xywz}+t}.\end{array}$ (4-8)

5. 总结

随着我国利率市场的不断开放，“二孩政策”的全面放开，国民经济水平的不断提升以及人们理财意识的不断增强，所以人寿保险业的未来发展前景非常乐观。对于保险公司来说，为了吸引客户，给寿险产品的保费进行合理的定价是十分重要的。现实生活中的利率不是静态的，而是不断地变化，所以我们选取“反射布朗运动 + 泊松过程”的组合建立双随机利率模型，在此基础上研究了完全离散险种的寿险精算模型。第一部分引言介绍了前人对寿险模型研究的状况，明确了本文研究的内容，第二部分介绍了生存模型以及随机过程的基础知识，第三部分推导出随机利率下一元寿险精算模型中的有关结论，第四部分讨论了随机利率下四元联合寿险精算理论的有关表达式。

本文为了公式推导的简单，均假设个体之间是相互独立的。但是在实际生活中一个个体的死亡，有很大概率会影响其余个体的剩余寿命，因此未来可以探究个体之间存在相依关系的多元寿险精算模型。对于四元联合寿险精算理论的研究，本文只讨论了联合生存状态和最后死亡者状态，没有对死亡顺序进行研究，因此未来可以考虑个体死亡顺序的寿险精算模型。

文章引用

吕嘉全. 随机利率下完全离散险种的寿险精算模型
Fully Discrete Life Insurance Actuarial Model with the Stochastic Interest Rate[J]. 应用数学进展, 2020, 09(06): 925-934. https://doi.org/10.12677/AAM.2020.96110

参考文献