Advances in Applied Mathematics
Vol.
10
No.
11
(
2021
), Article ID:
46357
,
6
pages
10.12677/AAM.2021.1011392
具有先序约束的平行机排序问题
陈雪1,廖礼琴1,张同全2*
1云南民族大学数学与计算机科学学院,云南 昆明
2云南民族大学预科教育学院,云南 昆明
收稿日期:2021年10月8日;录用日期:2021年10月29日;发布日期:2021年11月9日

摘要
根据财务系统中的回避原则,构造了具有先序约束的平行机排序问题的模型,目标函数为最小化最大负载,证明了具有先序约束的平行机排序问题是一个NP-完备问题。为之设计了LPTM算法,并分析了其近似比为 。
关键词
平行机,排序,先序约束,近似算法

Parallel Machine Scheduling Problem with Precedence Constraints
Xue Chen1, Liqin Liao1, Tongquan Zhang2*
1School of Mathematics and Computer Science, Yunnan Minzu University, Kunming Yunnan
2School of Preparatory Education, Yunnan Minzu University, Kunming Yunnan
Received: Oct. 8th, 2021; accepted: Oct. 29th, 2021; published: Nov. 9th, 2021

ABSTRACT
According to the avoidance principle in the financial system, a model of the parallel machine scheduling problem with precedence constraints is constructed, and the objective function is to minimize the maximum load, which is proved that the parallel machine scheduling problem with precedence constraints is an NP-complete problem. We design the LPTM algorithm and analyze its approximate ratio to .
Keywords:Parallel Identical Machines, Scheduling, Precedence Constraints, Approximation Algorithms

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在财务系统中,同一个服务者即可以核算,也可以总付。对于同一工件,服务者进行核算就不能进行总付,且每个工件的核算要在总付之前。因此,需要制定相应的分配策略,使得工件量较大时,尽可能在较短的时间完成工作。此问题实际上可以转化成具有先序约束的平行机排序问题。由于该问题在现实生活中有着广泛的应用,深受大家的重视,一直以来都有许多的研究者对此类问题进行研究。用Graham等 [1] 提出的三符号表示法来表示拟研究的排序问题。
在具有先序的平行机排序问题中,对于加工不允许被打断的情况Prot等 [2] 在2018年的一项调查中描述了先序约束结构是如何改变一个排序问题的复杂性的。Sarahí Báez等 [3] 在2019年对具有开始时间约束的平行机排序问题设计了混合元启发算法。2019年柴幸 [4] 对带有工件约束的平行机排序问题的近似算法进行了研究,考虑了m台平行机上工件带有链组约束的在线排序,工件具有相同的加工长度,目标是最小化最大完工时间。考虑了 的情形。证明该问题在线算法竞争比的下界为 ,其中当 时, 是方程 的唯一正根;当 时, 是方程 的唯一正根。其次给出达到该竞争比的最好可能的在线算法。
2021年Lee等 [5] 对于平行机的理想排序做了调查和总结,通过对比发现,经过几十年的研究,已经取得了一些研究成果,但对于具有先序约束的平行机排序问题找到最优排序依旧困难。 是Dolev等 [6] 研究的问题的一个特殊情况。本文所研究的问题相比较 ,不同点在于 。
Graham [7] 证明,如果没有优先约束,并且根据LPT (最长处理时间优先)算法对工件进行排序,
在LPT算法下的近似比为 ,受LPT算法的启发,本文针对具有先序约束的平行机排序问题设计了LPTM算法,并分析当每台机器只含有一个第一道工序时近似比为 ,当每台机器至少含两个第一道工序时近似比为 。
2. 问题描述
2.1. 问题的数学模型描述
2.1.1. 理论模型
m台机器,n个工件,每个工件i有两道工序,记为i1、i2,i1要先于i2完成,用符号表示,即 ,完成i1、i2的时间记为 ,,且i1与i2不能在同一台机器上加工。目标为将n个工件的两道工序分配到m台机器上,最后完工的机器运行时间达到最小。
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(1)表示目标函数,使负载最大的机器加工所用的时间最小,(2)表示i1完成之后i2的加工才可以开始,(3)表示同一个工件的不同工序不能在同一台机器上加工,(4)、(5)表示i1和i2在加工的过程中不会被打断,(6)表示i1或i2是否在第k台机器上加工,或者是否在第k台机器的第j个位置加工,若在则为1,反之为0,(7)表示i1和i2在不同机器上的加工时间相等,(8)表示i,k的取值范围。
2.2. 问题的NP-完全性证明
定理1具有先序约束的平行机排序问题是一个NP-完备问题。
证明:我们把2-划分问题的任何一个实例多项式归结到工件不同工序不能在同一台机器上加工的平行机排序问题的一个实例。
考虑2-划分问题的一个实例P:给定了n个数的集合 。问是否存在A一个划分 使得: ,,满足 ?
构造工件不同工序不能在同一台机器上加工的平行机排序问题的实例P'如下:
,,,,,.
下面证明论断:2-划分问题的实例P有解当且仅当工件不同工序不能在同一台机器上加工的平行机排序问题的实例P'有目标函数值为B的最优解。
(必要性)设2-划分问题的实例P有解为
,.
下面构造P'的可行解 。由于
说明 是P'有目标函数值为B的一个最优解。
(充分性)设工件不同工序不能在同一台机器上加工的平行机排序问题的实例P'有目标函数值为B的最优解 有
取 ,,则 ,说明2-划分问题有解 ,。
由于2-划分问题是NP-完全的 [7],说明,工件不同工序不能在同一台机器上加工的平行机排序问题的实例P'也是完全的。因此,工件不同工序不能在同一台机器上加工的平行机排序问题是一个NP-完备问题。
3. 算法设计思路
首先按LPT算法将i1 ( )安排在m台机器上,此时得到m个互不相交的集合 , 表示在第j台机器上加工的i1所组成的集合,加工 中的i1所用的时间为 ,。令集合 。
其次,以负载最大的机器加工时间 作为所有i2最早开始加工时间,此时相应会产生m个互不相交的集合 ,令集合 ,
表示在第j台机器上加工的i1对应的i2所组成的集合。
最后,依次将 中的i2按LPT算法分配到除第j台机器外的其他m-1台机器上加工。在分配 时,若 ,将大于其他机器加工时间所安排的 取出,按LPT算法排到除第k台机器与第m台机器外的其他m-2台机器上。反之将 中的i2按LPT算法分配到除第m台机器外的其他m-1台机器上。令 表示分配完所有i2,第j台机器加工i2的时间。此时,最大负载的机器加工时间为 。
4. 算法设计
LPTM
输入:具有先序约束的平行机排序问题的一个实例 。
Begin
输出:最大负载的机器所加工的时间 。
Step 1按LPT算法对n个工件的第一道工序进行分配,分配完成得最大负载机器所加工的总时间为
,得到集合 与 ,记此时 。
Step 2 ,m台机器加工i2的最早开始时间均为 。将 中的i2按LPT分配到除第k台及其外的m-1台机器,得到此时每台机器上加工的时间
。
Step 3 若 ,转Step 2,否则转Step 4。
Step 4 若 ,转4.1,否则转4.2。
4.1 若此时最大负载的机器为第m台机器,则取出多出的工件 ,按LPT规则排到除第j台和第m台机器外的其他机器上,否则,转Step 2。
4.2 输出最大负载的机器所加工的时间 。
End
例 考虑工件不同工序不能在同一台机器上加工的平行机排序问题,其中m = 4,n = 10, ,求其算法1排序及相应的时间表长。
OPT = 5 (如图1所示)
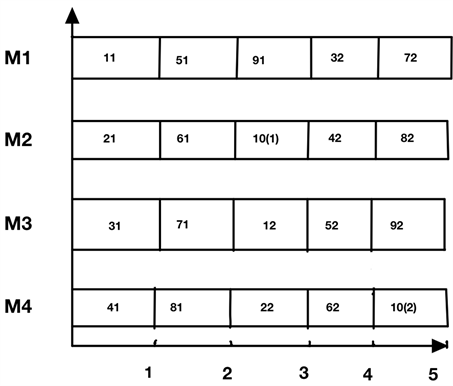
Figure 1. Example of parallel machine sequencing where different processes cannot be processed on the same machine
图1. 不同工序不能在同一台机器上加工的平行机排序实例
5. 算法的可行性分析
由于LPT算法的时间复杂度为 ,易得LPTM算法的时间复杂度也为 。
定理2 [8] 对于 ,LPT算法是 近似算法。
定理3 LPTM2算法是 近似算法。
证明:考虑负载最大的机器 ,令n1表示最后分配的i1,n2表示最后分配的i2。
因为
所以
得证。
注:当每台机器只含有一个第一道工序时近似比为 ,当每台机器至少含两个第一道工序时,由于 ,所以此时近似比为 。
6. 结语
根据财务系统中的回避原则,构造了具有先序约束的平行机排序问题的数学模型,参考LPT算法对两台及多台机器设计出LPTM算法来解决此类问题,并证明此问题是一个NP-完备问题,同时分析得算法的近似比。为财务系统中工作分配提供了新的思路,有一定的现实意义和应用价值。本文只研究了每个工件有两道工序的情形,后续还可以研究每个工件有超过两道工序以及每个工件的工序数不尽相同的情况。
文章引用
陈 雪,廖礼琴,张同全. 具有先序约束的平行机排序问题
Parallel Machine Scheduling Problem with Precedence Constraints[J]. 应用数学进展, 2021, 10(11): 3693-3698. https://doi.org/10.12677/AAM.2021.1011392
参考文献
- 1. Graham, R.L., Lawler, E.L., Lenstra, J.K., et al. (1979) Optimization and Approximation in Deterministic Sequencing and Scheduling: A Survey. Annals of Discrete Mathematics, 5, 287-326. https://doi.org/10.1016/S0167-5060(08)70356-X
- 2. Prot, D. and Bellenguez-Morineau, O. (2018) A Survey on How the Structure of Precedence Constraints May Change the Complexity Class of scheduling Problems. Journal of Scheduling, 21, 3-16. https://doi.org/10.1007/s10951-017-0519-z
- 3. Báez, S. and Angel-Belloa, F. (2019) A Hybrid Metaheuristic Algorithm for a Parallel Machine Scheduling Problem with Dependent Setup Times. Computers & Industrial Engineering, 131, 295-305. https://doi.org/10.1016/j.cie.2019.03.051
- 4. 柴幸. 带有工件约束的平行机排序问题的近似算法研究[D]: [博士学位论文]. 郑州: 郑州大学, 2019.
- 5. Jiang, X., Lee, K. and Pinedo, L. (2021) Ideal Schedules in Parallel Machine Settings. European Journal of Operational Research, 290, 405-806. https://doi.org/10.1016/j.ejor.2020.08.010
- 6. Dolev, D. and Warmuth, M.K. (1984) Scheduling Precedence Graphs of Bounded Height. Journal of Algorithms, 5, 48-59. https://doi.org/10.1016/0196-6774(84)90039-7
- 7. Graham, R.L. (1969) Bounds on Multiprocessing Timing Anomalies. SIAM Journal of Applied Mathematics, 17, 416-429. https://doi.org/10.1137/0117039
- 8. David, P.W. and David, B.S. (2010) The Design of Approximation Algorithms. Cambridge University Press, New York, 39-42.
NOTES
*通讯作者。