Open Journal of Nature Science
Vol.05 No.02(2017), Article ID:20733,13
pages
10.12677/OJNS.2017.52026
Analysis of Shear Stress Concentration of Slip System for Nickel-Based Single Crystal Superalloys
Wanchao Sun
Aircraft Strength Research Institute, Aero-Engine Strength Research Department, Xi’an Shaanxi

Received: May 6th, 2017; accepted: May 20th, 2017; published: May 27th, 2017

ABSTRACT
In order to perfect the crystal slip theory and its engineering application and evaluation of the low cycle fatigue and creep life model that developed on the crystal slip theory, the related definition of slip system shear stress concentration factor for nickel-based single crystal alloy was proposed .Through theoretical derivation and finite element method, the slip system stress concentration factor of nickel base single crystal superalloy was analyzed, it can be deduced that: 1) There exists obvious difference in stress concentration effect between isotropic alloy and nickel-based single crystal alloy. So it would be inappropriate to use the stress concentration coefficient of isotropic alloy to handle nickel-based single crystal alloy; 2) For plane problem, the shear stress concentration coefficient in slip system only determined by component’s shape and crystal orientation, and has nothing to do with the material elastic constants; 3) For nickel-based single crystal alloy, stress concentration coefficient is anisotropic with crystal orientation. Under the same shape and load conditions, stress concentration coefficient in [111] orientation takes its maximum, in [011] orientation second, and in [001] orientation the minimal.
Keywords:Stress Concentration, Slip System, Crystal Orientation, Nickel-Based Single Crystal, Shear Stress Concentration
镍基单晶高温合金滑移系剪应力集中分析
孙万超
中航工业飞机强度研究所,航空发动机强度研究室,陕西 西安
收稿日期:2017年5月6日;录用日期:2017年5月20日;发布日期:2017年5月27日

摘 要
为了完善晶体滑移理论及基于该理论而发展起来的低周疲劳寿命模型、蠕变寿命模型在工程中的应用及评价,提出了镍基单晶合金滑移系剪应力集中系数的相关定义。通过理论推导和有限元方法分析了镍基单晶高温合金的滑移系应力集中系数,得到以下结论:1) 各向同性材料与镍基单晶合金的应力集中效应有着明显的差异,采用各向同性材料应力集中系数处理镍基单晶合金材料是不合适的;2) 对于平面问题,滑移系剪应力集中系数只决定于构件的形状、晶体方向、而与材料的弹性常数无关;3)对于镍基单晶合金材料,应力集中系数具有晶体取向各向异性。形状与载荷条件相同下,[111]取向具有最大的应力集中系数,[011]取向次之,[001]取向最小。
关键词 :应力集中,滑移系,晶体取向,镍基单晶,剪应力集中系数

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
镍基单晶合金材料因其具有卓越的高温性能被用于先进航空、航天发动机涡轮叶片而受到材料学家、力学家及工程师的广泛关注和研究 [1] [2] [3] 。镍基单晶合金主要由γ'和γ相以共晶结合的形式组成,这两相都是面心立方体结构,整个晶体无晶界,γ'相总是在γ基体中共格析出。正是这种规律性的微观组织结构,使得镍基单晶合金在宏观上表现出力学性能的高度正交各向异性和疲劳损伤的高度取向相关性 [4] [5] [6] [7] 。
对比各向同性合金,镍基单晶合金的力学行为有着很大的差异,为了充分的利用其先进的性能,准确的预测镍基单晶合金构件的使用寿命至关重要。不准确的寿命计算,会导致不是材料的性能没有得到充分的利用,就是构件寿命没有达到指定的要求。目前学者对镍基单晶合金疲劳失效的研究,取得了很大的进展,然而这些研究绝大多数都是对其微观损伤的机理性研究 [8] [9] [10] 和基于材料标准试验件在单向应力状态下的疲劳寿命分析 [1] [2] 。孙万超、陆山对不同取向、带应力集中状态下镍基单晶合金构件的低周疲劳寿命进行了研究,发现考虑应力集中效应的疲劳预测寿命和不考虑应力集中效应的疲劳预测寿命相差487倍 [11] 。然而,该文章并未对镍基单晶高温合金滑移系剪应力集中系数的定义和分析进行研究。对于镍基单晶合金低周疲劳寿命在多轴应力状态考虑应力集中效应分析的文献还不够全面,在工程应用方面进行低周疲劳分析存在的问题还尚待研究。
应力集中现象普遍存在于各种工程结构中:起重机 [12] 、舰船 [13] 、高速铁路 [14] 、水利枢纽 [15] 、桥梁 [16] [17] 、航空发动机 [18] 。影响结构疲劳寿命的因素比较多,其中应力集中对结构疲劳寿命的影响最为显著 [19] [20] 。同时,可靠性作为产品质量的主要指标和最重要的技术指标之一,已经受到工程界的广泛重视。在实际工程结构中,应力集中的部位往往是最易被损坏的部位。因此应力集中是影响工程结构可靠性的一个重要因素。上世纪,结构、力学工程师对于传统的高温合金应力集中系数有了深入的研究。最近十几年,具有各种不同性能的新材料被广泛的应用,这些材料以其独特的性能逐步在某些领域替换传统高温合金,然而对这些材料的应力集中系数的研究没有跟上时代的步伐,对应力集中的认识基本停步在上世纪80~90年代。以至于目前对于镍基单晶合金的分析,往往采用各向同性材料应力集中系数手册计算单晶合金应力集中系数 [21] [22] 。
目前,对于镍基单晶这样特殊的正交各向异性材料,尤其是与滑移系相关的应力集中现象,据笔者所知尚无相关定义及分析。因此为了完善晶体滑移理论及基于该理论而发展起来的低周疲劳寿命模型、蠕变寿命模型在工程中的应用及评价,本文拟对滑移系剪应力集中现象进行深入的研究。
2. 滑移系剪应力集中系数定义
在一定程度上,滑移系的应力集中效应成为晶体滑移理论 [23] [24] 与基于该理论而发展起来的低周疲劳寿命模型、蠕变寿命模型之间的桥梁 [25] [26] 。晶体滑移理论及相应的低周疲劳寿命模型中均采用六面体({100}<110>)、八面体({111}<110>)和十二面体滑移系({111}<112>),分别包含12、6、12个滑移系 [26] 。本文选取具有代表性的八面体滑移系簇和十二面体滑移系簇为例对滑移系剪应力集中现象进行分析,见图1。各滑移系滑移面法向和滑移方向矢量见表1。本文定义滑移系剪应力集中系数相关概念和定义如下:
1) 应力集中处,A滑移系簇第α滑移系剪应力绝对值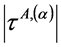 与适当选取的A滑移系簇第α滑移系基准剪应力绝对值
与适当选取的A滑移系簇第α滑移系基准剪应力绝对值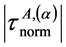 之比,定义为:A滑移系簇第α滑移系绝对理论剪应力集中系数,用符号
之比,定义为:A滑移系簇第α滑移系绝对理论剪应力集中系数,用符号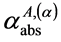 表示
表示
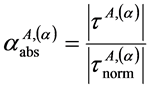 (1)
(1)
式中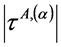 表示:应力集中构件在载荷作用下,客观存在的A滑移系簇第α滑移系剪应力绝对值。
表示:应力集中构件在载荷作用下,客观存在的A滑移系簇第α滑移系剪应力绝对值。 为适当选取的A滑移系簇第α滑移系基准剪应力,是人为规定的剪应力比的基准。
为适当选取的A滑移系簇第α滑移系基准剪应力,是人为规定的剪应力比的基准。
2) 应力集中处A滑移系簇的第α滑移系剪应力绝对值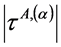 与适当选取的A滑移系簇中所有滑移系最大基准剪应力绝对值
与适当选取的A滑移系簇中所有滑移系最大基准剪应力绝对值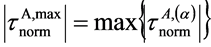 之比,定义为:A滑移系簇第α滑移系相对理论剪应力集中系数,即
之比,定义为:A滑移系簇第α滑移系相对理论剪应力集中系数,即
 (2)
(2)
3) 将A滑移系簇第α滑移系绝对(相对)理论剪应力集中系数与滑移系剪应力集中因素几何尺寸绘制的曲线,称为:A滑移系簇第α滑移系绝对(相对)理论剪应力集中系数曲线。
4) A滑移系簇的所有滑移系绝对(相对)理论剪应力集中系数曲线统称为:A滑移系簇绝对(相对)理论剪应力集中系数曲线。
5) A滑移系簇中最大滑移系剪应力对应的绝对(相对)理论剪应力集中系数曲线定义为:优先开启的A滑移系簇绝对(相对)理论剪应力集中系数曲线。
6) 比A滑移系簇最大剪应力绝对值小20%以内的滑移系对应的绝对(相对)理论剪应力集中系数曲线定义为:具有激活潜力的A滑移系簇绝对(相对)理论剪应力集中系数曲线。
对于应力集中构件,通过公式(1)绘制出A滑移系簇绝对理论滑移系剪应力集中曲线,能直观的看出该滑移系剪应力集中因素对所有滑移系应力集中程度的影响。缺点是:对所有滑移系簇的每个滑移系分别设定基准剪应力,显然会带来应用上的不便;某些滑移系的Schmid系数因子很小,会产生无穷小比无穷小的情况;应力集中因素对各滑移系的影响大小与各滑移系剪应力大小无关,该图不能直接得到该滑移系簇激活的滑移系及被激活的滑移系数目。通过公式(2)绘制出A滑移系簇相对理论滑移系剪应力集中系数曲线,能直观的看出A滑移系簇中被激活的滑移系及被激活的滑移系数目,并且能够直接得到未被激活的滑移系剪应力与最大剪应力的比值。缺点是:不能看出该应力集中因素对所有滑移系应力集中程度的影响。
3. 含中心圆孔的平板拉/压应力集中分析
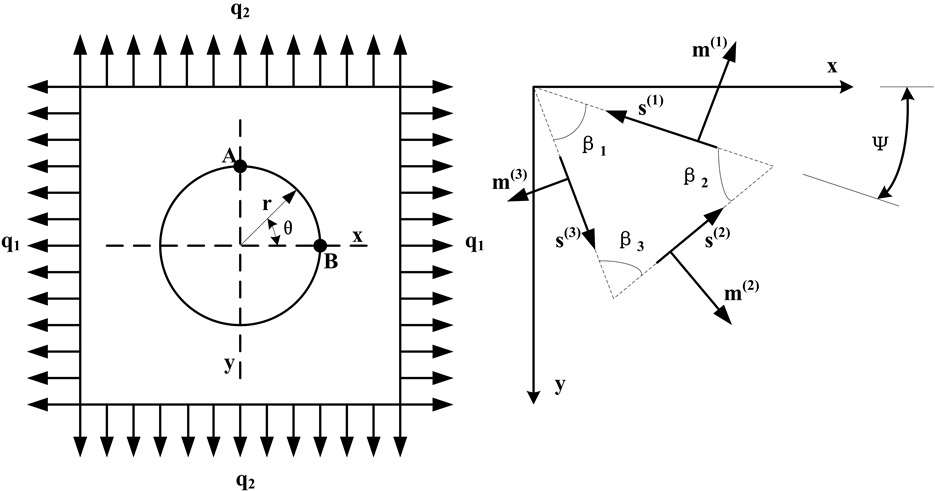
厚度为t的无限大板,有一个半径为r的圆孔。板承受沿x和y轴方向的匀布拉力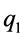 和
和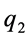 ,如图2(a)所示。晶体滑移理论为率相关本构模型,构件从初始受力状态起就发生着弹性变形和塑性的滑移,当构件变形处于较小阶段时,滑移系剪应力数值很小,此时的剪应变率呈幂级数减小,可以认为理论滑移系剪应力集中系数研究的阶段,正是弹性变形占据绝对主导地位时期的应力集中程度 [24] 。因此,可以采用
,如图2(a)所示。晶体滑移理论为率相关本构模型,构件从初始受力状态起就发生着弹性变形和塑性的滑移,当构件变形处于较小阶段时,滑移系剪应力数值很小,此时的剪应变率呈幂级数减小,可以认为理论滑移系剪应力集中系数研究的阶段,正是弹性变形占据绝对主导地位时期的应力集中程度 [24] 。因此,可以采用
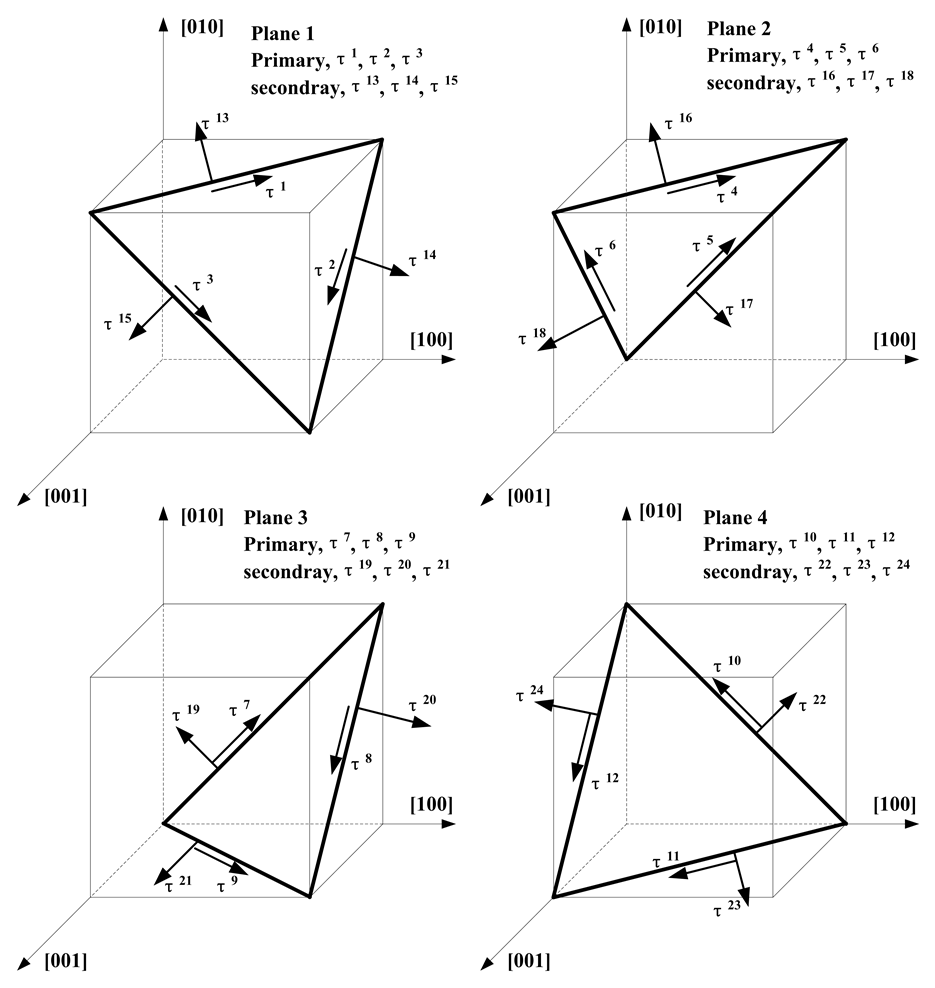
Figure 1. {111}<110> and {111}<112> families of slip directions
图1. 八面体滑移系簇和十二面体滑移系簇
Table 1. {111}<110> and {111}<112> slip systems
表1. 八面体、十二面体滑移系簇
 (A) (B)
(A) (B)
Figure 2. A plate with round hole and slip system for the plane problem
图2. 含一个圆孔的平板及平面问题的滑移系
弹性力学的方法研究未进入屈服的理论滑移系剪应力集中系数。
1) 按“小孔口问题”求解,利用弹性力学的方法可得到该无限大平板应力状态的基尔斯解答如下 [26] :
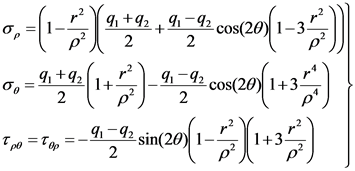 (3)
(3)
由应力分量的坐标变换式可以得到直角坐标系下的应力状态为:
 (4)
(4)
进一步可以求得该无限大平板应力状态的滑移系解答为:
 (5)
(5)
其中σ为用公式(4)所求得的应力张量,PA,(α)为A滑移系簇第α滑移系的Schmid因子,mA,(α)和sA,(α)分别为A滑移系簇第α滑移系的滑移方向矢量和滑移方向的法向矢量,如图2(b)所示。其中ψ为晶体生长方向与加载方向的夹角,β1、β2和β3分别为如图所示的滑移三角形之间的夹角。
取无穷远处的A滑移系簇第α滑移系剪应力绝对值 为基准剪应力,则(x2+y2=ρ2)处的A滑移系簇第α滑移系绝对理论剪应力集中系数可以表示为:
为基准剪应力,则(x2+y2=ρ2)处的A滑移系簇第α滑移系绝对理论剪应力集中系数可以表示为:
 (6)
(6)
2) 孔边(x2 + y2 = r2)处的应力状态为:
 (7)
(7)
取无穷远处的A滑移系簇第α滑移系剪应力绝对值 为基准剪应力,则孔边(ρ=r)的A滑移系簇第α滑移系绝对理论剪应力集中系数可以表示为:
为基准剪应力,则孔边(ρ=r)的A滑移系簇第α滑移系绝对理论剪应力集中系数可以表示为:
 (8)
(8)
3) 对含一个中心圆孔的有限大平板单向和双向拉伸(压缩)进行应力集中分析时,与含一个中心圆孔的无限大平板的分析是一样的,上述所有的公式(除了基准剪应力的选取外)都适用。
对于镍基单晶合金材料平面问题中的理论滑移系剪应力集中问题,由以上所推导的公式可知,A滑移系簇第α滑移系剪应力分布只决定于构件的形状、边界上的载荷条件、载荷方向与晶体生长方向的夹角及滑移系,而与材料的弹性常数无关。于是在试验应力分析中,对于可以简化为平面问题的构件,利用力学性质不同的镍基单晶材料制作模型,以代替真实镍基单晶材料制作的构件进行理论滑移系剪应力集中分析,对平面问题是精确的。
4. 含V型半圆沟槽的圆杆应力集中分析
4.1. 基准剪应力的选取
直径为D的圆杆,有V型沟槽,沟槽底部的曲率半径为r,圆杆的最小直径为d。当圆杆承受轴向载荷P时,滑移系剪应力的最大值发生在沟槽底部的A点,如图3所示。本节从轴向/等效、具有激活潜力的八面体(十二面体)滑移系簇相对理论剪应力集中系数的角度,采用晶体学本构模型 [24] ,分析镍基单晶材料V型缺口试棒应力集中问题。

Figure 3. A V shape niked test bar
图3. V型沟槽试棒
A滑移系簇第α滑移系相对理论剪应力集中系数与基准剪应力分别为:
 (9)
(9)
其中: 、
、 、
、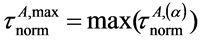 。
。
等效应力集中系数为:
 (10)
(10)
轴向应力集中系数为:
 (11)
(11)
4.2. 轴向/等效应力集中系数
本节分析了镍基单晶合金(DD3)V型缺口试棒轴向/等效应力集中系数及晶体取向相关性,其中图4分别为D/d = 1.2和1.4,不同开口角度、不同取向轴向/等效应力集中系数对比。
当D/d = 1.2,沿[001]、[011]、[111]取向拉伸或压缩V型缺口试棒,轴向/等效应力集中系数的取值范围分别为:
a) θ = 60˚:(1.649 − 3.299)/(1.528 − 2.818)、(1.786 − 3.636)/(1.987 − 3.835)和(2.289 − 4.268)/(2.250 − 4.268);
b) θ = 90˚:(1.430 − 3.264)/(1.331 − 2.785)、(1.574 − 3.611)/(1.753 − 3.785)和(1.961 − 4.355)/(1.928 − 4.294);
c) θ = 120˚:(1.433 − 2.887)/(1.320 − 2.323)、(1.579 − 3.236)/(1.758 − 3.421)和(1.953 − 3.916)/(1.916 − 3.884)。
当D/d = 1.4,沿[001]、[011]、[111]取向拉伸或压缩V型缺口试棒,轴向/等效应力集中系数的取值范围分别为:
a) θ = 60˚:(1.444 − 3.739)/(1.355 − 3.248)、(1.608 − 4.111)/(1.765 − 4.181)和(2.103 − 4.858)/(2.057 − 4.784);
b) θ = 90˚:(1.445 − 3.572)/(1.354 − 3.021)、(1.606 − 4.024)/(1.765 − 4.109)和(2.097 − 4.737)/(2.053 − 4.653);
c) θ = 120˚:(1.430 − 2.975)/(1.314 − 2.443)、(1.601 − 3.498)/(1.761 − 3.661)和(2.076 − 4.267)/(2.028 − 4.204)。

Figure 4. The axial/equivalent stress concentration factor in different orientation of a V shape niked test bar
图4. V型缺口试棒、不同取向的轴向/等效应力集中系数
由图4可以看出,轴向/等效应力集中系数随着2r/d的增大而单调递减;2r/d在(0, 0.1)区间变化时,应力集中系数变化激烈,并且随着D/d的增大,激烈程度也随着增大;2r/d大于0.1时,应力集中系数变化平缓。当θ一定时,轴向/等效应力集中系数随着D/d的增大而增大;当D/d一定时,轴向/等效应力集中系数随着θ的增大而减小。
镍基单晶合金的轴向、等效应力集中系数具有晶体取向相关性,相同的缺口参数下,应力集中系数,由[111]、[011]、[001]取向顺序依次减小。由图4可以看出,轴向应力集中系数与等效应力集中系数具有一定的差异,这是因为轴向应力不受周向应力的干扰,而等效应力为六个应力分量的联合,周向应力对等效应力产生不同程度的干扰,使得轴向应力集中系数曲线与等效应力集中系数曲线不再重合。
4.3. 八面体滑移系簇相对理论剪应力集中系数
由于V型缺口试棒几何参数较多,因此本节仅列出具有激活潜力的八面体滑移系簇相对理论剪应力集中系数曲线。如图5所示。
当D/d = 1.2,沿[001]、[011]、[111]取向拉伸或压缩V型缺口试棒,优先开启的八面体滑移系簇相对理论剪应力集中系数取值范围分别为
a) θ = 60˚:(1.685 − 3.182)、(1.936 − 3.372)和(2.704 − 4.713);
b) θ = 90˚:(1.479 − 3.113)、(1.700 − 3.451)和(2.367 − 4.985);
c) θ = 120˚:(1.508 − 2.667)、(1.706 − 3.073)和(2.402 − 4.336);
当D/d = 1.4,2r/d∈(0.02, 0.35)时,沿[001]、[011]、[111]取向拉伸或压缩U型缺口试棒,优先开启的八面体滑移系簇相对理论剪应力集中系数取值范围分别为
a) θ = 60˚:(1.548 − 3.581)、(1.740 − 3.843)和(2.646 − 5.836);
b) θ = 90˚:(1.550 − 3.453)、(1.740 − 3.817)和(2.645 − 5.534);
c) θ = 120˚:(1.517 − 2.879)、(1.725 − 3.364)和(2.615 − 4.959);
镍基单晶合金的八面体滑移系剪应力集中系数具有晶体取向相关性,[111]取向的八面体滑移系簇相对理剪应力集中系数最大,[011]取向次之,[001]取向最小,且随着2r/d的增大而单调减小。2r/d在(0, 0.1)区间变化时,八面体滑移系簇相对理论剪应力集中系数变化激烈,并且随着D/d的增大,激烈程度也随着增大;2r/d大于0.1时,八面体滑移系簇相对理论剪应力集中系数变化平缓。
4.4. 十二面体滑移系簇相对理论剪应力集中系数
图6为具有激活潜力的十二面体滑移系簇相对理论剪应力集中系数曲线。当D/d = 1.2,沿[001]、[011]、[111]取向拉伸或压缩V型缺口试棒,优先开启的十二面体滑移系簇相对理论剪应力集中系数取值范围分别为
a) θ = 60˚:(1.586 − 2.772)、(1.874 − 3.352)、(2.574 − 4.627);
b) θ = 90˚:(1.394 − 2.840)、(1.626 − 3.387)、(2.255 − 4.748);
c) θ = 120˚:(1.402 − 2.534)、(1.619 − 3.007)、(2.260 − 4.122);
当D/d = 1.4,2r/d∈(0.02,0.35)时,沿[001]、[011]、[111]取向拉伸或压缩V型缺口试棒,优先开启的十二面体滑移系簇相对理论剪应力集中系数取值范围分别为
a) θ = 60˚:(1.420 − 3.467)、(1.677 − 3.765)、(2.477 − 5.429);
b) θ = 90˚:(1.419 − 3.294)、(1.678 − 3.711)、(2.472 − 5.217);
c) θ = 120˚:(1.399 − 2.704)、(1.652 − 3.238)、(2.448 − 4.625);
镍基单晶合金的十二面体滑移系剪应力集中系数具有晶体取向相关性,[111]取向的十二面体滑移系簇相对理论剪应力集中系数最大,[011]取向次之,[001]取向最小,且随着2r/d的增大而单调减小。2r/d在(0, 0.1)区间变化时,十二面体滑移系簇相对理论剪应力集中系数变化激烈,并且随着D/d的增大,激烈程度也随着增大;2r/d大于0.1时,十二面体滑移系簇相对理论剪应力集中系数变化平缓。
对比图4~图6可以看出,轴向应力集中系数、等效应力集中系数和滑移系剪应力集中系数具有很大
的差异,这是因为轴向应力不受周向应力的干扰,而Hill等效应力和滑移系剪应力由六个应力分量计算得出 [13] [14] ,但是滑移系剪应力与Hill等效应力的计算方法显然是不同的,使得轴向应力集中系数曲线、等效应力集中系数曲线与滑移系剪应力集中系数曲线不再重合。由此可以得出,利用不同的方法评估镍基单晶合金部件的疲劳、蠕变寿命和裂纹扩展,应采用相应的应力集中系数作为准则设计模拟试件。

Figure 5. The relative theoretic stress concentrated coefficient in different orientation of {111}<110> slip systems
图5. 不同取向的八面体滑移系簇相对理论剪应力集中系数

Figure 6. The relative theoretic stress concentrated coefficient in different orientation of {111}<112> slip systems
图6. 不同取向的十二面体滑移系簇相对理论剪应力集中系数
5. 结论
基于晶体滑移理论,对镍基单晶合金滑移系剪应力集中系数进行了定义、计算和分析,得到以下结论:
1) 各向同性材料与镍基单晶合金的应力集中效应有着明显的差异,采用各向同性高温合金应力集中系数处理镍基单晶合金是不合适的。
2) 对于平面问题,滑移系剪应力分布只决定于构件的形状和晶体方向,而与材料的弹性常数无关。于是在试验应力分析中,对于可以简化为平面问题的构件,利用力学性质不同的镍基单晶材料制作模型,以代替真实镍基单晶材料制作的构件进行滑移系剪应力集中分析,对平面问题是精确的。
3) 对于镍基单晶合金材料,形状与载荷条件相同下,[111]取向具有最大的优先开启潜力的理论滑移系剪应力集中系数、轴向应力集中系数和等效应力集中系数,[011]取向次之,[001]取向最小。即[111]取向具有最高的缺口敏感性,[011]取向次之,[001]取向最小。
4) 各取向的优先开启潜力的理论滑移系剪应力集中系数、轴向应力集中系数和等效应力集中系数有着较大的差异。轴向应力集中系数不能反映缺口试棒的多轴应力状态,而滑移系剪应力集中系数和等效应力集中系数可以反映出多轴应力状态。
5) 利用不同的方法评估镍基单晶合金部件的疲劳、蠕变寿命和裂纹扩展,应采用相应的应力集中系数作为准则设计模拟试件。
文章引用
孙万超. 镍基单晶高温合金滑移系剪应力集中分析
Analysis of Shear Stress Concentration of Slip System for Nickel-Based Single Crystal Superalloys[J]. 自然科学, 2017, 05(02): 190-202. http://dx.doi.org/10.12677/OJNS.2017.52026
参考文献 (References)
- 1. Arakere, N.K. (2004) High-Temperature Fatigue Properties of Single Crystal Superalloys in Air and Hydrogen. ASME Journal of Engineering for Gas Turbines and Power, 126, 590-603. https://doi.org/10.1115/1.1501075
- 2. Wahi, R.P., Auerswald, J., Mukherji, D., Dudka, A., Fecht, H.J. and Chen, W. (1997) Damage Mechanisms of Single Andpolycrystalline Nickel Base Superalloys SC16 and IN738LC under High Temperature LCF Loading. International Journal of Fatigue, 19, S89-S94. https://doi.org/10.1016/S0142-1123(97)00038-8
- 3. Dalal, R.P., Thomas, C.R. and Dardi, L.E. (1984) The Effect of Crystallographic Orientation on the Physical and Mechanical Properties of an Investment Cast Single Crystal Nickel-Base Superalloy. TMS-AIME, Warrendale, 185-197.
- 4. Taylor, G.I. and Elam, C.F. (1925) The Plastic Extension and Fracture of Aluminum Crystals. Proceedings of the Royal Society, 108, 25-51. https://doi.org/10.1098/rspa.1925.0057
- 5. Schmid, E. (1935) Plasticity of Crystal. Oxford University Press, New York.
- 6. Myoung, G.L., Wagoner, R.H. and Kim, S.J. (2008) Comparative Study of Single Crystal Constitutive Equations for Crystal Plasticity Finite Element Analysis. International Journal of Modern Physics, 22, 5388-5393. https://doi.org/10.1142/S0217979208050541
- 7. Czech, N. and Stamm, W. (1996) Thermal Cycle Fatigue Properties of Coated and Uncoated Single Crystal Superalloy. Surface and Coatings Technology, 86, 15-21. https://doi.org/10.1016/S0257-8972(96)02947-7
- 8. Antelo, M.A., Johnson, P.K., Ostolaza, K.M. and Bressers, J. (1998) Analysis of the Fracture Behaviour of an Aluminide Coating on a Single-Crystal Superalloy under Tensile Conditions. Materials Science and Engineering, A247, 40- 50. https://doi.org/10.1016/S0921-5093(98)00477-8
- 9. Czech, N. and Stamm, W. (1996) Thermal Cycle Fatigue Properties of Coated and Uncoated Single Crystal Superalloy. Surface and Coatings Technology, 86, 15-21. https://doi.org/10.1016/S0257-8972(96)02947-7
- 10. Gui, T.S., Wang, M.G., Li, T., Qian, B.J. and Xie, J. (2010) Influence of TCP Phase and Its Morphology on Creep Properties of Single Crystal Nickel-Based Superalloys. Materials Science and Engineering, A527, 5444-5451. https://doi.org/10.1016/j.msea.2010.05.027
- 11. 孙万超, 陆山. 考虑应力集中的镍基单晶合金低周疲劳公式[J]. 应用力学学报, 2013, 33(2): 273-277.
- 12. 张超, 秦义校, 李艳青, 等. 桥式起重机箱型主梁典型缺陷应力集中分析[J]. 机械工程与自动化, 2012(1): 122- 123.
- 13. 王子. 典型船舶焊接接头应力集中系数有限元分析[J]. 船海工程, 2012, 43(3): 4-6.
- 14. 何川, 封坤, 晏启祥. 高速铁路水下盾构隧道管片内力分布规律研究[J]. 铁道学报, 2012, 34(4): 101-109.
- 15. 王志良, 申林方, 姚激. 开槽预应力闸墩应力集中特性研究[J]. 水利水电技术, 2012, 43(9): 46-49.
- 16. 陈亮, 郑廷银. 腹板几何尺寸变化对梯形波纹腹板工字钢梁应力集中的影响[J]. 南京工业大学学报, 2012, 34(4): 138-144.
- 17. 段钢文. 桥梁结构钢筋应力集中、疲劳研究[J]. 黑龙江交通科技, 2012(2): 96.
- 18. 航空工业部科学技术委员会. 应力集中系数手册[M]. 北京: 高等教育出版社, 1990.
- 19. 董志航, 廖志忠. 理论应力集中系数的有限元求法[J]. 航空兵器, 2005(3): 15
- 20. 陆山, 王春光, 陈军. 任意最大梯度路径轮盘模拟件设计方法[J]. 航空动力学报, 2010, 25(9): 2000-2005.
- 21. Filippini, M. (2011) Notched Fatigue Strength of Single Crystals at High Temperature. Procedia Engineering, 10, 3787-3792. https://doi.org/10.1016/j.proeng.2011.04.618
- 22. 赵萍, 何清华, 李维, 等. 单晶切口试样低周疲劳特性研究[J]. 航空动力学报, 2010, 25(11): 2632-2636.
- 23. Asaro, R.J. (1983) Crystal Plasticity. ASME Journal of Applied Mechanics, 50, 921-934. https://doi.org/10.1115/1.3167205
- 24. 孙万超, 陆山. 用于单晶叶片应力分析的滑移本构模型研究[J]. 推进技术, 2012, 33(5): 754-759.
- 25. Arakere, N.K. and Swanson, G. (2002) Effect of Crystal Orientation on Fatigue Failure of Single Crystal Nickel Base Turbine Blade Superalloys. ASME Journal of Engineering for Gas Turbines and Power, 124, 161-176. https://doi.org/10.1115/1.1413767
- 26. 孙万超. 镍基单晶合金力学性能及低周疲劳分析与应用[D]: [博士学位论文]. 西安: 西北工业大学, 2013.
