Open Journal of Natural Science
Vol.
10
No.
04
(
2022
), Article ID:
53574
,
9
pages
10.12677/OJNS.2022.104060
镜质组反射率梯度与古地温梯度间的关系研究
——以陕北榆神矿区5-2富油煤层为例
马青华1,张学梅1,赵晓东2,魏亚玲3,郝静远4
1西安思源学院,能源及化工大数据应用教学研究中心,陕西 西安
2北京德秦技术开发有限公司,北京
3宁夏叁方煤质检测科技有限公司,宁夏 银川
4西安交通大学化工学院,陕西 西安
收稿日期:2022年6月13日;录用日期:2022年7月6日;发布日期:2022年7月13日

摘要
利用吴氏煤变质热动力学方程计算5-2富油煤层的变质温度为54.2℃~76.6℃,并画出古地质时间、镜质组反射率和变质温度三者之间的关系图。为了解释极大的埋深或地温梯度差距,利用不超过深成变质的镜质组反射率梯度值 < 0.06%/百米重新计算古地温梯度。根据已知5-2富油煤层的地质数据,计算得到在R0 = 0.53%, = 0.06%/百米,t = 193百万年时产生的地温梯度是9.14℃/百米为最大值,计算得到在R0 = 0.53%, = 0.01%/百米,t = 205百万年时产生的地温梯度是1.55℃/百米为最小值。即使是在相同的地质条件范围内(古地质时间、镜质组反射率、埋深),也能够满足转化为不同煤化阶段所需的温度。
关键词
煤变质热动力学方程,变质温度,埋深温度,镜质组反射率梯度,温度梯度

Relationship between Vitrinite Reflectance Gradient and Paleogeothermal Gradient
—Taking 5-2 Oil Rich Coal Seam in Yushen Mining Area in Northern Shaanxi as an Example
Qinghua Ma1, Xuemei Zhang1, Xiaodong Zhao2, Yaling Wei3, Jingyuan Hao4
1Energy and Chemical Industry Big Data Application Teaching and Research Center, Xi’an Siyuan University, Xi’an Shaanxi
2Beijing Deqin Technology Development Co., Ltd., Beijing
3Ningxia Sanfang Coal Quality Testing Technology Co., Ltd., Yinchuan Ningxia
4School of Chemical Engineering, Xi’an Jiaotong University, Xi’an Shaanxi
Received: Jun. 13th, 2022; accepted: Jul. 6th, 2022; published: Jul. 13th, 2022

ABSTRACT
A coal metamorphic thermal dynamics equation has been used to calculate the paleo-geo temperature of 5-2 oil-rich coal seam, and the results are 54.2˚C~76.6˚C, and shown in a three dimensional drawing of paleo-geo time, vitrinite reflectance and metamorphic temperature. In order to account for the great buried depth or paleo-geo temperature gradient gaps, the paleo-geo temperature gradient was recalculated using a vitrinite reflectance gradient of <0.06%/100 m. Based on the known geological data of the 5-2 oil-rich coal seam, the paleo-geo temperature gradient generated at R0 = 0.53%, = 0.06%/100 m, t = 193 million years is 9.14˚C/100 m, and the paleo-geo temperature gradient generated at R0 = 0.53%, = 0.01%/100 m, t = 205 million years is 1.55˚C/100 m which is the minimum. Even within the same geological conditions (paleo-geo time, vitrinite reflectance, buried depth), it can meet the temperature required for conversion into different metamorphism stages.
Keywords:Coal Metamorphic Thermal Dynamics Equation, Metamorphic Temperature, Buried Depth Temperature, Vitrinite Reflectance Gradient, Temperature Gradient

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 前言
陕西省有五大煤田,分别是陕北侏罗纪煤田、陕北石炭–二叠纪煤田、陕北三叠纪煤田、黄陇侏罗纪煤田、渭北石炭–二叠纪煤田。其中陕北侏罗纪煤田的榆神矿区赋存的富油煤资源量最高,并且煤层埋藏条件、开采条件及煤质等方面是最好的。为了提升我国油气自主保障能力,实现煤炭清洁高效利用,推进“碳达峰、碳中和”的目标,学者们针对榆神矿区富油煤(地质概况、煤质特征、煤化程度等)进行了研究 [1] [2] [3] [4] [5]。影响煤变质的因素有温度、压力和时间。温度是影响煤变质的主要因素,地温越高,煤化程度越高。时间也是影响煤变质的另一重要因素,精确评价古地温及古地温梯度是地质研究的重要内容,也是一直探讨尚未解决的课题。本文将试图对煤变质热动力学、富油煤深成变质的古地温计算以及镜质组反射率梯度与古地温梯度间的关系加以研究。
2. 地质基本数据
陕西省榆林市境内的榆神矿区是成煤期约为距今2.05亿年~1.59亿年的中生代侏罗纪早中期,是低阶富油煤产区之一。该矿区位于构造简单的鄂尔多斯盆地东北部,区内尚未发现大断层,亦无岩浆活动,基本确认为深成变质。榆神矿区现有三层可采富油煤层,从地表往下分别是位于延安组第四段顶部的2−2号煤层、位于延安组第三段顶部的3−1号煤层、和位于延安组第一段顶部的5−2号煤层。现以5−2号煤层为例做煤变质热动力学变质温度计算、以及镜质组反射率梯度与古地温梯度间的关系研究,其基本地质数据列于表1。
Table 1. Geological overview of coal seam 5−2 in Yushen mining area [1]
表1. 榆神矿区5−2号煤层的地质概况 [1]
虽然知道延安组第一段的古地质时间早于延安组第四段的古地质时间,但却不知道延安组第一段至延安组第四段所对应的具体古地质时间,则人为地将中生代侏罗纪早中期2.05亿年~1.59亿年分成四个等分时间段对应于延安组第一段至延安组第四段。
3. 煤变质热动力学温度
因为镜质体反射率(Ro)表征了煤在温度、时间影响下的组分和性质变化(即煤化程度变化),所以煤变质程度、温度、和时间三者之间是相互影响。根据杨起的论述已有计算公式或图表揭示把煤级、温度和受热的持续时间的例子 [6] [7] [8] [9] [10]。
吴冲龙在煤变质作用热动力学分析一文中 [6],根据 Bostick的曲线 [11] [12] 和中国热史较单一的松辽、鄂尔多斯、二连等盆地的中、新生界实测数据采用双重回归的方法来建立T (古地质温度,热力学温度paleogeo temperature K)-t (古地质时间,百万年paleogeo time Ma)-Ro (镜质组反射率% Vitrinite reflectance)经验方程,简称为“吴氏煤变质热动力学方程”。该方程含三元函数,所以可以在有任意2个已知量的前提下求第3个量。古地质时间是原文在建立公式时所用的时间表述,也可以理解为成煤期。
(1)
式中:T:温度,K;t:古地质时间,百万年;R0:镜质体平均反射率
现将利用方程(1)已知镜质组反射率和古地质时间计算得到的温度称为煤变质热动力学温度,简称为变质温度,并记为Tm (metamorphic temperature)。也有几篇文章讨论了一些相关问题 [13] [14] [15]。图1表示按表2中所列的古地质时间范围和镜质组反射率范围计算的变质温度。
Table 2. Paleogeological time, vitrinite reflectance and metamorphic temperature range of coal seam 5−2
表2. 5−2煤层的古地质时间、镜质组反射率和变质温度范围
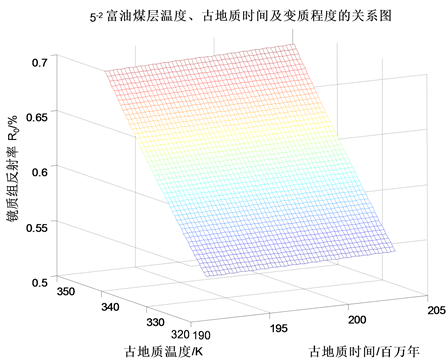
Figure 1. 5−2 relationship between temperature, paleogeological time and metamorphic degree of oil rich coal seams
图1. 5−2富油煤层温度、古地质时间及变质程度的关系图
从图1中可以得出在上述条件下,5−2煤层的最小变质温度在最长地质时间和最小变质程度下计算所得,即327.2 K,或54.2℃。而最大变质温度在最短地质时间和最大变质程度下计算所得,即349.6 K,或76.6℃。以上显示的煤变质温度范围符合“大量资料表明转化为不同煤化阶段所需的温度大致为:褐煤40~50℃,长焰煤小于100℃”的结论。从图1中的曲线变化的趋势可以看出古地质温度和古地质时间与变质程度是正相关,即随着温度的升高,变质程度是增大;随着时间的延长,变质程度也是增大。同时还可以看出温度对变质程度的影响远大于时间对变质程度的影响。
4. 煤埋深温度
地温随深度的增加而升高是一普遍规律。但由于不同地区的地质构造条件、深部地壳结构及地下水活动等等因素的影响,其表现的形式则有很大不同。所以除了求变质温度外,还有就是求埋深温度,Tb (Buried Temperature)。
(2)
式中:T0:地表恒温,℃;H:埋深,米;DT:地温梯度,℃/百米。
埋深温度是埋深和地温梯度的函数。根据中国地温分布的基本特征中关于鄂尔多斯盆地地温梯度为2.88℃/百米。以及表1中5−2煤层的平均镜质组反射率为0.62,以及最长古地质时间为205百万年,计算得到古地温应该为67.63℃。将上述数据代入埋深温度公式,并取地表恒温为15℃,求得的相应埋深为1827米。与表1中的埋深相差1113~1767米。
为了解释这样大的埋深差距,以前采用“地层被剥蚀”来补偿,但是从未考虑古地温梯度。既然热源会有不同,以正常地温为热源、以岩浆为热源、以热液或热水为热源、以深大断裂上导的高温为热源,那么古地温梯度与现地温梯度有差别,以及各地区的古地温梯度之间有差别就不足为奇。早期曾经有一个理论“冷却系时法” [16]。该方法是把地球看作不断冷却的热体,以现今地温为基准,用经验系数对今地温进行校正得到古地温。这种方法推出:地史过程中地温梯度不变,那么地史上各时代的热流值也是衡定的,这显然是不可能的。地球的不断冷却必然表现为温度、地温梯度和热流的同时减小。
假设埋深是基本正确,那么也可以计算出正确的古地温梯度应为7.36℃/百米。根据变质温度、变质时间、以及埋深都与变质程度正相关的知识,将方程(1)做以下数学处理:
(3-1)
(3-2)
(3-3)
(3-4)
(4)
古地温梯度是古地质时间、镜质组反射率、和镜质组反射率梯度的函数。尽管镜质组反射率值的大小是地史过程中各时代不同温度的作用与所经历的时间的总累积效应,但如果造成这两个温度的差别是同一个自变量,即为相差一百米的两个不同镜质组反射率值(%/百米镜质组反射率梯度),此时就得出古地温梯度了。根据方程4,与古地温梯度的变化有关的可以是镜质组反射率或镜质组反射率梯度。以下就分别加以讨论。5−2富油煤层的镜质组反射率的变化范围已经列在表1中。镜质组反射率梯度的变化范围可以根据“以正常地温为热源促使煤进行深成变质的镜质组反射率梯度一般低于0.06%/百米” [7]。
4.1. 固定镜质组反射率的古地温梯度
先讨论固定镜质组反射率,变化古地质时间和镜质组反射率梯度造成的古地温梯度。可以用以下公式表示:
(4-1)
具体条件为R0 = 0.53%, = 0.01~0.06%/百米,t = 193~205百万年。所得结果用图2表示。
从图2中的曲线变化的趋势可以看出镜质组反射率梯度和古地质时间与温度梯度是有关系的,即随着镜质组反射率梯度的升高,温度梯度是增大;随着时间的延长,温度梯度也是减少。同时还可以看出镜质组反射率梯度对温度梯度的影响远大于时间对温度梯度的影响。在固定镜质组反射率时,最小的温度梯度产生于最长地质时间和最小镜质组反射率梯度的条件下。如R0 = 0.53%, = 0.01%/百米,t = 205百万年时产生的温度梯度是1.55℃/百米为最小值。而最大的温度梯度产生于最短地质时间和最大镜质组反射率梯度的条件下。如R0 = 0.53%, = 0.06%/百米,t = 193百万年时产生的温度梯度是9.14℃/百米为最大值。
根据方程(2)可得固定镜质组反射率时的埋深温度,并画于图3。其中地表恒温为15℃,地质时间为193百万年,R0 = 0.53%, = 0.01~0.06%/百米,埋深 = 200~725米。
从图3中的曲线变化的趋势可以看出镜质组反射率梯度和埋深与埋深温度是正相关,即随着镜质组反射率梯度的升高,埋深温度是增大;随着埋深的加大,埋深温度也是增大。同时还可以看出镜质组反射率梯度对埋深温度的影响稍稍大于埋深对埋深温度的影响。根据图3中的数据,可以得出:利用不超过深成变质的镜质组反射率梯度值(<0.06%/百米)重新计算古地温梯度,即使是在相同的地质条件范围内(古地质时间、镜质组反射率、埋深),也能够满足转化为不同煤化阶段所需的温度。
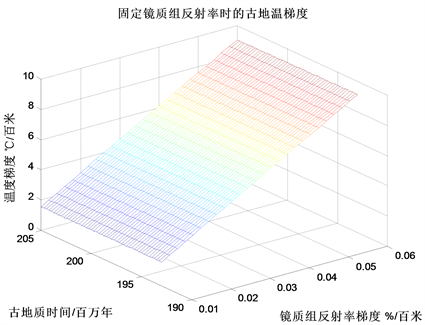
Figure 2. Paleogeothermal gradient with fixed vitrinite reflectance
图2. 固定镜质组反射率时的古地温梯度
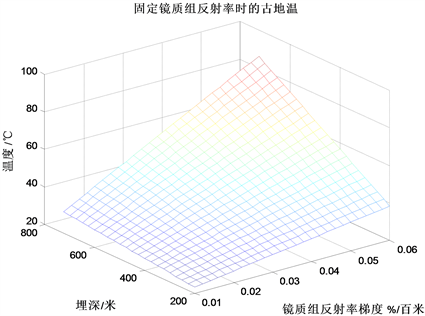
Figure 3. Paleogeo temperature at fixed vitrinite reflectance
图3. 固定镜质组反射率时的古地温
4.2. 固定镜质组反射率梯度的古地温梯度
可以用以下公式讨论固定镜质组反射率梯度,变化古地质时间和镜质组反射率造成的古地温梯度:
(4-2)
具体条件为R0 = 0.53~0.69%, = 0.06%/百米,t = 193~205百万年。所得结果用图4表示。
从图4中的曲线变化的趋势可以看出镜质组反射率和古地质时间与温度梯度是是有关的,即随着镜质组反射率的升高,温度梯度是减少的;随着时间的延长,温度梯度也是减少的。同时还可以看出镜质组反射率对温度梯度的影响远大于时间对温度梯度的影响。在固定镜质组反射率梯度时,最大的温度梯度产生于最短地质时间和最小镜质组反射率的条件下。如R0 = 0.53%, = 0.06%/百米,t = 193百万年时产生的温度梯度是9.14℃/百米为最大值。而最小的温度梯度产生于最长地质时间和最大镜质组反射率的条件下。如R0 = 0.68%, = 0.06%/百米,t = 205百万年时产生的温度梯度是7.67℃/百米为最小值。
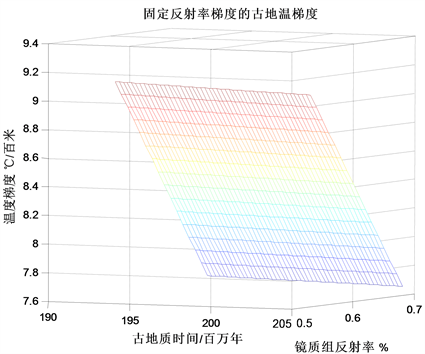
Figure 4. Paleogeothermal gradient with fixed reflectance gradient
图4. 固定反射率梯度的古地温梯度
同样可得固定反射率梯度,计算古地温随埋深和镜质组反射率的变化。根据方程(2)可得固定镜质组反射率梯度时的埋深温度,并画于图5。其中地表恒温为15℃,地质时间为193百万年,R0 = 0.53~0.69%, = 0.06%/百米,埋深 = 200~725米。
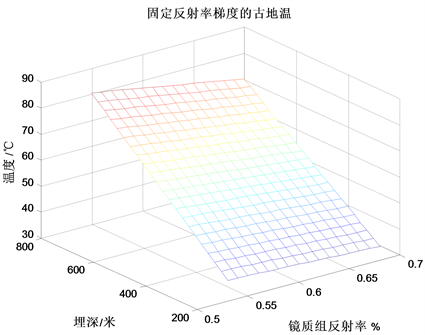
Figure 5. Paleotemperature with fixed reflectance gradient
图5. 固定反射率梯度的古地温
从图5中的曲线变化的趋势可以看出镜质组反射率和埋深与埋深温度是相关,即随着镜质组反射率的升高,埋深温度是下降的;随着埋深的加大,埋深温度却是增大。同时还可以看出镜质组反射率对埋深温度的影响小于埋深对埋深温度的影响。根据图5中的数据,可以得出:利用不超过深成变质的镜质组反射率梯度值(<0.06%/百米)重新计算古地温梯度,即使是在相同的地质条件范围内(古地质时间、镜质组反射率、埋深),也能够满足转化为不同煤化阶段所需的温度。
5. 结论
1) 利用吴氏煤变质热动力学方程计算古地质温度,称为变质温度。将5−2富油煤层的古地质时间、镜质组反射率和变质温度三者之间的相互关系用图加以显示。随着古地质时间的增长和变质温度的升高,煤的变质程度是加深的。这种方法所计算的古地质温度在54.2℃~76.6℃。
2) 取5−2煤层的平均镜质组反射率为0.62%,以及最长古地质时间为205百万年,计算得到变质温度应该为67.63℃。根据中国地温分布的基本特征中关于鄂尔多斯盆地地温梯度为2.88℃/百米,并取地表恒温为15℃,求得的相应埋深为1827米,远远大于该煤层的最大埋深。如果5−2煤层的埋深和变质温度应该为67.63℃是计算基础,那么正确的古地温梯度应为7.36℃/百米,远远大于现鄂尔多斯盆地地温梯度。为了解释这样大的埋深或地温梯度差距,除采用“地层被剥蚀”来补偿,还考虑对古地温梯度重新进行计算。
3) 古地温梯度是古地质时间、镜质组反射率和镜质组反射率梯度的函数。根据已知5−2富油煤层的地质数据(镜质组反射率、古地质时间、埋深),并将镜质组反射率梯度 < 0.06%/百米,计算得到在R0 = 0.53%, = 0.06%/百米,t = 193百万年时产生的地温梯度是9.14℃/百米为最大值,计算得到在R0 = 0.53%, = 0.01%/百米,t = 205百万年时产生的地温梯度是1.55℃/百米为最小值。利用不超过深成变质的镜质组反射率梯度值(<0.06%)重新计算古地温梯度,即使是在相同的地质条件范围内(古地质时间、镜质组反射率、埋深),也能够满足转化为不同煤化阶段所需的温度。
文章引用
马青华,张学梅,赵晓东,魏亚玲,郝静远. 镜质组反射率梯度与古地温梯度间的关系研究——以陕北榆神矿区5-2富油煤层为例
Relationship between Vitrinite Reflectance Gradient and Paleogeothermal Gradient—Taking 5-2 Oil Rich Coal Seam in Yushen Mining Area in Northern Shaanxi as an Example[J]. 自然科学, 2022, 10(04): 489-497. https://doi.org/10.12677/OJNS.2022.104060
参考文献
- 1. 许婷, 李宁, 姚征, 等. 陕北榆神矿区富油煤分布规律及控制因素[J/OL]. 煤炭科学技术, 2022, 50(3): 161-168. https://doi.org/10.13199/j.cnki.cst.MTQY21-018
- 2. 杨甫, 段中会, 马丽, 等. 陕西省富油煤分布及受控地质因素[J/OL]. 煤炭科学技术. https://doi.org/10.13199/j.cnki.cst.20231-0531
- 3. 师庆民, 米奕臣, 王双明, 等. 富油煤热解流体滞留特征及其机制[J/OL]. 煤炭学报, 2022, 47(3): 1329-1337. https://doi.org/10.13225/j.cnki.jccs.XR21.1734
- 4. 马丽, 王双明, 段中会, 等. 陕西省富油煤资源潜力及开发建议[J]. 煤田地质与勘探, 2022, 50(2): 1-8. https://doi.org/10.12363/issn.1001-1986.21.10.0592
- 5. 师庆民, 王双明, 王生全, 等. 神府南部延安组富油煤多源判识规律研究[J/OL]. 煤炭学报. https://kns.cnki.net/kcms/detail/11.2190.TD.20211228.1329.004.html
- 6. 吴冲龙, 杨起, 刘刚, 等. 煤变质作用热动力学分析的原理与方法[J]. 煤炭学报, 1997, 22(3): 225-229.
- 7. 杨起. 中国煤的叠加变质作用[J]. 地学前缘, 1999(S1): 1-8.
- 8. 杨起. 中国煤变质研究[J]. 地球科学, 1989, 14(4): 341-345.
- 9. 杨起, 吴冲龙, 汤达祯, 等. 中国煤变质作用[J]. 地球科学, 1996, 21(3): 311-319.
- 10. 曹代勇, 李小明, 邓觉梅. 煤化作用与构造-热事件的耦合效应研究——盆地动力学过程的地质记录[J]. 地学前缘, 2009, 16(4): 52-60.
- 11. Bostick, N.H., Cashman, S.M., McCulloh, T.H., et al. (1979) Gradients of Vitrinite Reflectance and Present Temperature in the Los Angeles and Ventura Basins, California. In: Oltz, D.F., Ed., Low Temperature Metamorphism of Kerogen and Clay Minerals, Pacific Section, SEPM (Society for Sedimentary Geology), Los Angeles, 65-96.
- 12. Hood, A., Gutjahr, C.C.M. and Heacock, R.H. (1975) Organic Metamorphism and the Generation of Petroleum. Bulletin—American Association of Petroleum Geologists, 59, 986-996. https://doi.org/10.1306/83D91F06-16C7-11D7-8645000102C1865D
- 13. 张学梅, 李东, 马青华, 等. 变质煤化与提质煤化热动力学雏议[J]. 地球科学前沿, 2021, 11(5): 561-569. https://doi.org/10.12677/ag.2021.115051
- 14. 张学梅, 李东, 马青华, 等. 煤变质热动力学方程的初步评判[J]. 地球科学前沿, 2021, 11(6): 827-834. https://doi.org/10.12677/ag.2021.116077
- 15. 张学梅, 李东, 马青华, 等. 温度-时间-煤变质程度的定量计算[J]. 地球科学前沿, 2021, 11(7): 937-946. https://doi.org/10.12677/ag.2021.117089
- 16. 韩永辉. 一种新的古地温梯度计算方法-Yij校正系数法[J]. 地球科学-中国地质大学学报, 1988, 13(1): 107-113.
