Finance
Vol.
11
No.
04
(
2021
), Article ID:
43969
,
14
pages
10.12677/FIN.2021.114036
沪深300股指期权定价实证研究——基于BS、CEV、Heston模型的对比分析
张翔*,李治#
南开大学经济学院,天津
收稿日期:2021年6月6日;录用日期:2021年6月21日;发布日期:2021年7月20日

摘要
为研究沪深300股指期权定价,本文在对BS、CEV、Heston模型进行了理论分析和欧式期权定价解析式推导后,针对不同模型使用了不同的方法进行参数估计并实现了模型定价。最后本文借由对称平均绝对百分比误差(sMAPE)作为误差衡量指标,得出了实证结论:1) 三个模型对期权的估值整体呈现高估的态势,整体拟合优度CEV模型 > BS模型 > Heston模型;2) 从虚实期权角度来看,三个模型均对实值期权拟合效果更好,对虚值期权而言CEV模型拟合效果最好,对实值期权而言Heston模型拟合效果最好;3) 进一步探究发现,BS模型和CEV对短到期期限、低价值的期权拟合效果相对较好,Heston模型对低执行价、短到期期限、低价值的期权拟合效果较好。
关键词
沪深300股指期权,波动率,BS模型,CEV模型,Heston模型

An Empirical Study on the Pricing of CSI 300 Index Options—Based on BS, CEV, and Heston Models
Xiang Zhang*, Zhi Li#
School of Economics, Nankai University, Tianjin

Received: Jun. 6th, 2021; accepted: Jun. 21st, 2021; published: Jul. 20th, 2021

ABSTRACT
In order to study the CSI 300 stock index option pricing, after theoretical analysis of the BS, CEV, and Heston models and analytical derivation of European option pricing, different methods are used for parameter estimation and model pricing for different models. Finally, this paper uses the symmetric mean absolute percentage error (sMAPE) as the error measurement index to draw the empirical conclusions: 1) The valuation of options by the three models is generally overestimated, and the overall goodness of fit: CEV model > BS model > Heston model; 2) From the perspective of out-of-the-money/real options, the three models are better for real options; The CEV model has the best fitting effect for out-of-the-money options, and the Heston model has the best fitting effect for real-valued options; 3) Further exploration found that the BS model and CEV have a relatively better fitting effect on short-expiration and low-value options, and the Heston model has a relatively better fitting effect on low-strike, short-expiration, and low-value options.
Keywords:CSI 300 Stock Index Options, Volatility, BS Model, CEV Model, Heston Model

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
期权是金融衍生品市场的重要组成部分,其本质上是一种合约,赋予了持有人在未来以某一特定价格买入或卖出某一资产权利。期权本质上是依托于现货而存在的,对于期权而言最核心的内容就是定价。合理定价的期权能丰富金融市场,为投资者提供对冲、保值的手段;而若期权定价偏离了公允价值,则会诱发套利行为的发生,严重会波及现货市场,造成股市动荡。
2020年中我国A股市场整体在动荡中上行,而期权作为一种能提供风险对冲功能的衍生品,在2020年也备受青睐。于2019年12月23日推出的沪深300股指期权是我国第一只股指期权,其意义不言而喻。我国各大证券交易所多次要求各做市商做好期权的风险管理工作,主要参考指标是Delta、Vega、Gamma等希腊值。但是这些希腊值仅是期权定价模型的附属品,要想准确的计算出期权的市场价值,还是应当首先从定价模型入手。因此本文基于BS、CEV、Heston模型,对沪深300期权定价进行了实证研究。
2. 文献综述
已有文献中一般预测金融资产波动率的模型有两类:历史波动率模型和内含波动率模型。历史波动率的代表模型就是条件异方差GARCH模型,是由T. Bollerslev [1] 于1986年在Engel提出的ARCH模型(1982)的基础上拓展提出的,GARCH模型相比ARCH模型更能体现出金融资产的长期记忆性。在此之后越来越多的学者对GARCH模型进行了优化,如1991年Nelson [2] 提出EGARCH模型和Glosten等 [3] 于1993年提出的GJR-GARCH模型,能较好的解决股票波动率的“杠杆效应”问题”。在随机波动率模型的研究上,Heston [4] 最早于1993年基于随机波动率给出了欧式期权的定价模型;而蒋祥林等 [5] 于2005年基于Bayes原理对随机波动率SV-N和SV-T模型进行了研究,并通过实证发现随机波动率模型优于GARCH模型。在隐含波动率领域Henry A. Latané和Richard J. Rendleman Jr [6] 于1976年最早通过实证研究了隐含波动率模型的拟合效果,并认为隐含波动率模型优于当时的历史波动率模型。郑振龙等 [7] 于2010年通过对不同的模型的预测效果进行对比分析,得出内含波动率模型更适合预测长期波动率,而GARCH模型更适合预测短期波动率的结论。倪中新等 [8] 于2020年对上证50 ETF进行实证,发现由BS公式推导出的内含波动率–执行价曲线对股票收益具有显著的预测能力。
目前期权定价模型主要可分为四类:BS模型、BS替代模型、随机波动率模型和IVF模型。BS模型是期权定价领域的基石,最早由Black等 [9] 于1973年提出,该模型最基本的假设就是股票价格服从几何布朗运动。此模型的提出,极大地促进了金融衍生品的发展。BS替代模型用其他连续扩散过程代替几何布朗运动或者在连续的运动过程中附加跳跃性,这些过程统称为levy过程。其中,Cox John C和Ross Stephen A [10] 在1976年提出了CEV(常方差弹性模型)模型,此模型在几何布朗运动基础上赋其予维纳过程项前的系数S一个β次方的权重,由此模拟资产价格概率分布左端肥尾( )或右端肥尾( )的情况。Merton Robert C [11] 在1976年把跳跃过程加入到连续的运动过程中,即默顿跳跃–连续模型,该模型给出的分布左右端均肥大。第三类是随机波动率模型,即假设波动率是随时间变化的。Heston [4] 于1993年提出随机波动率Heston模型,其假设 ,而v服从一个CIR过程。P. Hagan等 [12] 在2002年提出了SARS模型,这种模型最大的优点是可以很好地拟合波动率微笑。最后一类IVF(隐含波动率函数)模型,该模型能够做到使期权价格和市场价格完全匹配,由B. Dupire [13]、E. Derman [14] 和M. Rubinstein [15] 于1994年提出,并给出了波动率函数 的解析式,在实际应用中IVF模型需每天利用期权数据对参数进行校正,也因此该模型对简单期权和部分奇异期权均有高精度的拟合效果,但不适合用于长期预测和实证研究。因此本文选取了前三类模型中的代表模型做实证对比研究。
沪深300股指期权推出时间较短,因此当前对于其定价实证领域研究的文章屈指可数,其中较有代表性的是张传涛 [16] 于2020年引入SVI波动率模型对沪深300股指期权进行定价,其中利用Quasi-Explicit方法对SVI模型实现了参数估计,结果显示结合了SVI模型的二叉树模型的定价效果更加精确。
综合来看,本文的主要贡献和创新主要是:1、选用当前研究文献较少的我国第一只股指期权作为实证研究样本,是对我国股指期权定价领域研究空白的补充;2、选取了三类不同模型中的代表模型:经典的BS模型、BS替代模型中的典型模型CEV模型、随机波动率模型中的典型模型Heston模型,着眼于研究不同模型的差异,以及对于股指期权价值的不同拟合效果。3、三类模型均使用简洁且精确的解析式法实现定价,同时在解析式法参数估计上的一些难点和复杂过程利用Python编写代码实现,为国内期权市场定价提供参考。
3. 模型构造与欧式期权定价解析式推导
3.1. BS模型
BS模型 [9] 是最经典的期权定价模型,其在期权定价领域基石的地位毋庸置疑,尽管近年来一直因为其严格的适用假设一直被诟病,但在我国许多期权交易机构仍在使用BS模型对期权进行估值。
BS模型认为对于任一时刻的股价有:
(1)
将其代换为对数股价形式,可得到:
(2)
也可以将其写为一个几何布朗运动过程:
(3)
其中u为期望收益率率、 为波动率,W为维纳过程:
(4)
其中 为标准正态分布
由于欧式看跌期权可由看涨期权价值和看涨看跌平价公式得到,故在此及下文中仅研究看涨期权的解析式。那么由风险中性定价可得欧式看涨期权价格:
(5)
要求解 ,可以先求解 。假设 服从正态分布,标注差为w,均值为m,定义 ,那么Q的密度函数 ,那么
(6)
对 一项进行整理:
(7)
带入 可得:
(8)
求出积分可得:
(9)
在上式基础上令 ,,即可得到欧式看涨期权的定价公式:
(10)
其中:
(11)
3.2. CEV模型
CEV模型 [10] 是BS模型的替代模型,其用另一个levy过程替代了BS模型所假设的几何布朗运动过程。
根据上文中所讨论内容,在BS模型中:
(12)
而在CEV模型中,引入了一个权重 ,使得股票价格服从以下扩散过程:
(13)
Cox John C.和Ross Stephen A.在1976给出了 的近似估计值为:
(14)
为BS模型中所使用的固定波动率,也即几何布朗运动下的波动率。
在CEV模型中,当 时,股票价格服从几何布朗运动,此时即为BS模型。
当 时, 随股票价格下降而上升,此时对应的情况即为隐含波动率为执行价格K递减函数的波动率微笑。如下右图所示,虚线所代表与对数收益率具有相同均值和标准差的正态分布,而实线为左图所示递减隐含波动率下的对数收益率概率分布。可见此时对数收益率的分布具有明显尖顶、左肥尾、右瘦尾的特征,见图1。

Figure 1. Diminishing volatility smile
图1. 递减型波动率微笑
时, 随股票价格上升而上升,此时对应的情况即为隐含波动率为执行价格K递增函数的波动率微笑。其图像正好与递减型波动率微笑相反,可见此时对数收益率的分布具有明显尖顶、右肥尾、左瘦尾的特征,见图2。
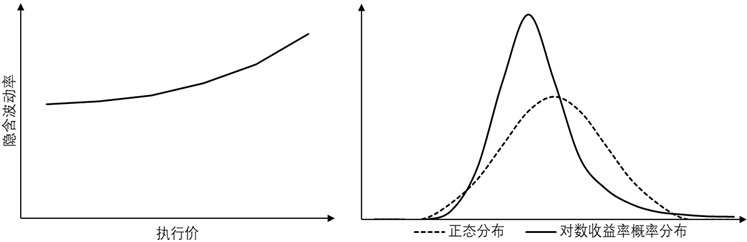
Figure 2. Increasing volatility smile
图2. 递增型波动率微笑
此时依然可以利用风险中性定价原理 得出CEV模型对欧式看涨期权的定价解析式,但在实际处理上十分困难,在此借助另一种方法求解——无套利均衡定价:
首先先了解伊藤过程,形如:
(15)
其中a、b为变量x和时间t的函数,W为维纳过程,那么上述过程就被定义为伊藤过程,几何布朗运动过程就是一个伊藤过程。
数学家K. Ito [17] 于1951年发现了有关该扩散过程的一个重要结论——伊藤引理。伊藤引理指出,对于一个漂移率为a,方差率为b2的伊藤过程,一个关于变量x和时间t的函数G服从以下过程:
(16)
可见上述过程也是一个伊藤过程。
现在推导CEV模型欧式看涨期权的解析式,设一个欧式看涨期权的价值为f,其为现货价格S和时间t的函数,由于CEV模型所假设的 过程为一个伊藤过程,由伊藤引理可得:
(17)
为了进行无套利定价,可以构造一个组合消除风险,即消除维纳过程。考虑这样一个组合P,由一个看涨期权空头和 数量的标的股票多头组成,那么P的价值为:
(18)
那么 的扩散过程为:
(19)
可见 中无维纳过程,是一个无风险组合。定义无风险利率为 ,那么由无套利原理有:
(20)
整理得:
(21)
由此得到了求解CEV模型欧式期权定价解析式的微分方程,对于看涨期权,关键边界条件为:
时, (22)
带入微分方程可解得当 时:
(23)
时:
(24)
其中:
(25)
为非中心 分布(24)
3.3. Heston模型
Heston模型是随机波动模型的代表模型之一,最早由Steven L. Heston [4] 于1993年发表的论文中提出。
在随机波动模型中,波动率不是一个固定变量而是随时间变化的,可表示为:
(26)
而在Heston模型中,令:
(27)
同时令:
(28)
这是一个CIR过程, 指长期方差率,v表示资产方差率,在该模型中v以k的速度被拉向长期方差率 当 趋于无限时, 期望值趋于 ;
而 也是一个伊藤过程,类似于上文对CEV模型的处理方法,由伊藤引理和无套利原理可得:
(29)
其中 为波动率风险的价格,为不可观测量,Heston定义其值为 ,同时证明了等价鞅测度下将其放在风险中性世界中可得 ,得以消除此项。
直接解这个方程很困难,Heston猜测Heston模型的欧式看涨期权定价解析式具有和BS解析式相似的形式:
(30)
如果已知 、 特征函数,那么通过傅里叶逆变换可得:
(31)
代表被积函数实数部分, ,i为虚数单位;Heston假定 、 的特征函数具有如下形式:
(32)
由(29)、(31)、(32)可得常微分方程:
(33)
初始条件:
(34)
可以解得:
,且:
(35)
其中 为两个维纳过程 、 的相关系数; 是 回归至 的速度; 是波动率的波动率,也就是 的方差。如果上述参数满足 ,那么过程 会是严格的正数。
[ ]是给定的参数,而[ ]是需要估计的参数。
3.4. BS、CEV、Heston模型理论对比
首先三个模型最本质的区别就是对股价的变动使用了不同的扩散过程去拟合
在BS模型中假设股价服从几何布朗运动过程:
(36)
而CEV模型在此基础上加了一个权重 ,同时对波动率也在BS模型基础上进行了近似替代,因而能较好地拟合隐含波动率为执行价格K递增或递减函数的波动率微笑:
(37)
Heston模型不再假定波动率固定,而是认为其是随时间变动的一个变量,同时使用5个参数对波动率的变动情况进行模拟,因而能够较好的拟合大部分股票的时变波动率:
(38)
此外无论是BS、CEV还是Heston模型,它们都能通过风险中性方法或无套利均衡原理得到对应的欧式期权定价解析式,但BS的定价解析式最为简洁,Heston模型最复杂。此外若要使用三个模型的欧式期权定价解析式进行定价,除可直接获得的四个参数[ ]外,BS模型还需估计波动率 ,CEV模型需估计 和 ,Heston模型需估计[ ]五个参数,因而在具体的参数估计方法的选择上也有差异。
4. 参数估计
4.1. 数据选取
参数估计部分的数据选取自2019年12月23日~2020年3月19日81只沪深300股指期权数据及其对应现货数据收盘价数据,其范围涵盖了不同的执行价、上市日期和到期期限,具有较好的随机性,数据来源Wind数据库。而2020年3月20号至2021年3月20日的数据将用于后文的模型拟合优度检验,故在此部分不使用。
4.2. BS模型参数估计——基于历史内含波动率
BS模型需要的参数包括[ ],其中[ ]是给定的,唯一需要估计的是一个固定年波动率 ,由于本文需要估计的是一个长期的波动率,综合考虑本文选取内含波动率模型进行估计。
在具体操作中,本文使用BS模型下的BS公式在给定真实市值、执行价、现货价、无风险利率、到期期限下,反推得到81只期权的内含波动率,求平均得到固定年波动率估计值 。
4.3. CEV模型参数估计——基于迭代法
CEV模型所需的参数在BS模型的基础上还有一个权重 。本文利用2020年3月19日之前的81只期权数据,使用迭代法设置估计精度为0.01,不断迭代减小模型预测值与真实值的误差,得到 的估计值1.61,迭代过程见图3。
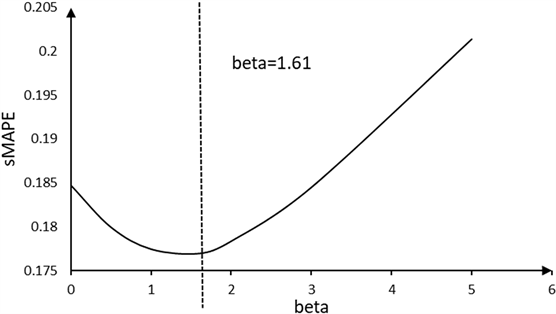
Figure 3. Optimal beta iteration process curve
图3. 最优beta迭代过程曲线
进而可以得到 的估计值
(39)
4.4. Heston模型参数估计——基于模拟退火算法
Heston模型同样需要给定[ ],而[ ]是需要估计的参数,而由于同时需要估计五个参数,估计CEV模型 值的所用的迭代法不再适用,因此可借助Python进行模拟退火算法,这是一种在一个大空间内寻找最优解的一般方法。模拟所使用的历史期权数据来自2020年3月19日以前上市的81只期权,其中算法具体参数设置见表1。
Table 1. Important parameter settings of simulated annealing algorithm
表1. 模拟退火算法重要参数设置
在经过10,862轮模拟后,满足了终止条件接受新解后的函数值变化连续小于0.001达到次数101次,此时温度为0.035188,输出参数最优解,见表2。
Table 2. Estimated values of parameters of the Heston model
表2. Heston模型各参数估计值
5. 误差分析
在估计了三个期权定价模型的参数后,即可利用本文理论基础部分列出的理论部分列出的对应的欧式看涨期权定价解析式进行定价。在该部分本文选用2020年3月20日~2021年3月20日的40只看涨期权数据,其范围涵盖了不同的执行价、上市日期和到期期限,具有较好的随机性。
由于不同期权价值相差较大,且同时存在正负误差,为了更科学的比较模型拟合优度,综合考虑本文选取对称平均绝对百分比误差(sMAPE)作为模型拟合效果的检验指标:
(40)
对于单个期权计算时,采用对称绝对百分比误差(sAPE):
(41)
其中 为模型的预测值, 为真值,基于此可以得出各模型拟合情况,见表3 (c为期权市场价值(单位:元),F为模型预测价值,sAPE为模型预测误差)。
Table 3. BS, CEV, Heston model prediction results and errors
表3. BS、CEV、Heston模型预测结果及误差
从上述实证结果来看,三个模型对期权的估值均呈现高估的态势,且BS模型和CEV模型单个期权估计结果很接近。此外综合来看,三个模型的sMAPE排序为: 。接下来探究模型对虚值期权和实值期权分别拟合效果,见表4。
Table 4. The fitting effect of the model on out-of-the-money/real options
表4. 模型对虚值期权和实值期权拟合效果
结果显示三个模型均对实值期权拟合效果更好,其中CEV模型对虚值期权拟合效果最好,Heston模型对实值期权拟合效果最好。对于此外为了进一步研究各个模型拟合效果的规律性,分别用三个模型的误差对c(真实价值:百元)、K(执行价:千元)、T(到期时间:年)进行回归,得到表5所示结果。
Table 5. Analysis of the influence of different factors on the goodness of model fit
表5. 不同因素对模型拟合优度影响分析
其中***、**和*分别表示在1%、5%和10%的水平上显著。先看真实价值对三个模型估计结果的影响,在5%的显著性水平下BS模型和CEV模型的预测误差受期权真实市值影响显著,而Heston模型在10%的显著性水平上显著,且三者系数均为正值,说明三个模型均对于价值较小的期权预测精度更高。
而执行价K对Heston模型在5%的显著性水平上显著,系数为正,说明其对执行价较小的期权预测精度较高。
到期时间T对于三个模型影响均在1%的显著性水平上显著,且系数为正,说明三个模型均对到期期限低的期权价值预测效果更好。
6. 结论
本文基于BS、CEV、Heston模型,使用解析式的方法,对沪深300股指期权进行了实证研究。通过以对称平均绝对百分比误差(sMAPE)作为误差指标的分析实证发现,三个模型对期权的估值均呈现高估的态势,且BS模型和CEV模型单个期权估计结果很接近,其中CEV模型拟合效果最好,其次为BS模型,Heston模型最差。从虚实期权角度来看,三个模型均对实值期权拟合效果更好,对虚值期权而言CEV模型拟合效果最好,对实值期权而言Heston模型拟合效果最好。进一步探究发现,BS模型和CEV对短到期期限、低价值的期权拟合效果相对较好,Heston模型对低执行价、短到期期限、低价值的期权拟合效果较好。
从实证结果可以发现, 为1.61的CEV模型拟合效果最好,而时变波动率的Heston模型拟合效果最次,说明沪深300股指期权存在一定的递增型波动率微笑现象,而时变波动率的特征较弱。
同时不仅模型整体拟合优度存在差异,模型的拟合优度还会随期权的虚实值状态和到期期限等等因素变动。对于沪深300而言,CEV模型对其虚值期权拟合效果最好,而Heston模型对实值期权的拟合效果十分出色,这也提醒市场对于期权定价而言,选用模型时要考虑多方位因素。
总的来说,中国的期权市场还处于前期发展阶段,目前市场BS模型的应用仍是主流。但是市场瞬息万变,宏观政策、市场噪音,或是像疫情这类突发重大事件等等都有可能使得股价呈现出大幅偏离几何布朗运动假设,沪深300股指期权作为一只几乎与疫情同时诞生的期权更是如此。因此研究期权定价中其时变性、跳跃性等非正态特征尤为重要。本文仅以三类模型对沪深300股指期权定价进行实证对比研究,希望可对我国期权市场发展贡献绵薄之力。
文章引用
张 翔,李 治. 沪深300股指期权定价实证研究——基于BS、CEV、Heston模型的对比分析
An Empirical Study on the Pricing of CSI 300 Index Options—Based on BS, CEV, and Heston Models[J]. 金融, 2021, 11(04): 319-332. https://doi.org/10.12677/FIN.2021.114036
参考文献
- 1. Bollerslev, T. (1986) Generalized Autoregressive Conditional Heteroscedasticity. Journal of Econometrics, 31, 307-327. https://doi.org/10.1016/0304-4076(86)90063-1
- 2. Nelson, D.B. (1991) Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica, 59, 347-370. https://doi.org/10.2307/2938260
- 3. Glosten, L.R., Jagannathan, R. and Runkle, D.E. (1993) On the Relation be-tween the Expected Value and the Volatility of the Nominal Excess Return on Stocks. Journal of Finance, 48, 1779-1801. https://doi.org/10.1111/j.1540-6261.1993.tb05128.x
- 4. Heston, S.L.A. (1993) Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. Review of Financial Studies, 6, 327-343. https://doi.org/10.1093/rfs/6.2.327
- 5. 蒋祥林, 王春峰. 基于贝叶斯原理的随机波动率模型分析及其应用[J]. 系统工程, 2005, 23(10): 22-28.
- 6. Latané, H. (1976) Standard Deviations of Stock Price Ratios Implied in Option Prices. The Journal of Finance, 31, 369- 381. https://doi.org/10.1111/j.1540-6261.1976.tb01892.x
- 7. 郑振龙, 黄薏舟. 波动率预测: GARCH模型与隐含波动率[J]. 数量经济技术经济研究, 2010, 27(1): 140-150.
- 8. 倪中新, 郭婧, 王琳玉. 上证50ETF期权隐含波动率微笑形态的风险信息容量研究[J]. 财经研究, 2020, 46(4): 155-169.
- 9. Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637-654. https://doi.org/10.1086/260062
- 10. Cox, J.C. and Ross, S.A. (1976) The Valuation of Options for Alternative Stochastic Processes. North-Holland, 3, 145- 166. https://doi.org/10.1016/0304-405X(76)90023-4
- 11. Merton, R.C. (1976) Option Pricing When Underlying Stock Returns Are Discontinuous. North-Holland, 3, 125-144. https://doi.org/10.1016/0304-405X(76)90022-2
- 12. Hagan, P., Kumar, D., Lesniewski, A. and Woodward, D. (2002) Managing Smile Risk. Wilmott, 9, 84-108.
- 13. Dupire, B. (1994) Pricing with Smile. Risk, 2, 18-20.
- 14. Derman, E. and Kani, I. (1994) Riding on a Smile. Risk, 2, 32-39.
- 15. Rubinstein, M. (1994) Implied Bi-nomial Trees. Journal of Finance, 7, 771-818. https://doi.org/10.1111/j.1540-6261.1994.tb00079.x
- 16. 张传涛. 基于SVI模型的沪深300股指期权定价实证研究[D]: [硕士学位论文]. 青岛: 山东科技大学, 2020.
- 17. Ito, K. (1951) On Stochastic Differential Equations. Memoirs of the American Mathematical Society, No. 4, 1-51. https://doi.org/10.1090/memo/0004
