Pure Mathematics
Vol.08 No.01(2018), Article ID:23650,7
pages
10.12677/PM.2018.81014
The Inflations of Finite Cyclic Groups
Lan Du, Pinhong Long*
School of Mathematics and Statistics, Ningxia University, Yinchuan Ningxia
*通讯作者。

Received: Jan. 9th, 2018; accepted: Jan. 24th, 2018; published: Jan. 31st, 2018

ABSTRACT
In this paper, some properties of inflations of groups are given. Moreover, a necessary and sufficient condition for an inflation of a group to be a left L-semigroup is proved. Finally, we obtain the basic conclusions of finite cyclic groups.
Keywords:Finite Cyclic Group, Inflation of Group, Commutative Group
有限循环群的膨胀
杜兰,龙品红*
宁夏大学数学统计学院,宁夏 银川

收稿日期:2018年1月9日;录用日期:2018年1月24日;发布日期:2018年1月31日

摘 要
本文给出了群膨胀的一些性质,然后证明了群膨胀是左L-半群的一个充要条件。最后,给出了有限循环群膨胀的基本性质。
关键词 :有限循环群,群的膨胀,交换半群

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设S为一个半群,T为S的子半群, 为S到T的映射。如果对于任意 有 ,对于任意 有 ,那么称S为它的子半群T的膨胀,称 为S到T的膨胀映射。如果半群S是群G的膨胀,那么S一定是拟正则半群。若拟正则半群S的幂等元集合E为S的理想,则称S为E-理想拟正则半群(见 [1] [2] )。
由对于半群S,如果 有单位元,那么S是 的膨胀(见 [3] )。设 是半群S中的元素,如果S中的元素 使得 ,那么称 (见 [4] )。设S为半群, 。若对任意 有 ,则称 为S的强幂等元。设S为周期半群,若S的幂等元皆为强幂等元,则称S为强周期半群(见 [5] )。本文主要研究有限循环群膨胀的基本性质。为此,首先考虑半群的一些等价关系,然后给出了群膨胀的一些性质,并且证明群膨胀是左L-半群的一个充要条件。
设S是半群, , , 表示S上的二元关系( [6] ):
下面我们定义半群上的等价关系。
定义 1.1.设S是半群, ,规定
引理 1.2.设S是半群, ,则 , 和 都是S上的等价关系,并且 , , 。
引理 1.3.如果S是交换半群, ,那么 ,但是 。
例 1.4.令半群 ,则由乘法运算有
则 -类 -类 -类 。并且 , , , 。
命题 1.5.设S是半群, ,如果 ,那么有
证明由 得 。于是
因此, 。
命题 1.6.设S是半群, , 。如果 ,那么有
证明如果 ,那么 , 。于是
同理, 。
命题 1.7.设S是半群,e是S的一个幂等元, ,如果 ,那么
证明根据 ,则 。于是
命题 1.8.设半群S只有一个幂等元e, 。如果 ,那么 。
证明根据 ,则
既然S只有一个幂等元e,则 。
命题 1.9.设半群S只有一个幂等元e, 。则
证明先证必要性。如果 ,那么有 使得 。则 。
再证明充分性。如果 ,那么有 使得 。于是
既然S只有一个幂等元e,则 , 。因此 。
2. 群的膨胀
在本节中,将给出关于群膨胀的一些性质。
定理 2.1.设S为交换群G的膨胀, 。如果 ,那么 。
证明由S为交换群G的膨胀, 得 。如果 ,那么 。于是
因此 。
定理 2.2.设S为交换群G的膨胀, 。如果 ,那么 。
证明由S为交换群G的膨胀, 得 。于是 , ,故存在 使得 , 。由 得到 。于是
定理 2.3.设S为交换群G的膨胀, 。则 的充分必要条件是 。
证明充分性显然。在此仅仅证明必要性。由S为交换群G的膨胀,得 。如果 ,那么 。于是 , ,故 。
定理 2.4.设S为交换群G的膨胀, 。如果 , , , ,那么 , 。
证明由 , , , 得
于是 。
由S为交换群G的膨胀知 ,于是存在 使得 , ,其中e为G的单位元,所以
同理 ,即 ,并且 。
定理 2.5.设S为群G的膨胀,e为G的单位元。如果e为S的强幂等元,那么 ,并且对S中的任意元素s有 。
证明设g是G中的任意元素由e为S的强幂等元得
,而
。故
,即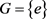 .
.
由S为群G的膨胀得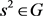 ,
, ,
,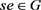 ,因此
,因此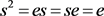 。
。
推论 2.6.设S为群 的膨胀,那么S是强周期半群。
的膨胀,那么S是强周期半群。
定理 2.7. 设S为群G的膨胀,e为G的单位元。则对S中的任意元素s有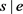 。
。
定理 2.8.设S为群G的膨胀,e为G的单位元。如果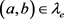 ,那么对S中的任意元素s有
,那么对S中的任意元素s有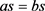 ,
,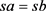 。
。
定理 2.9.设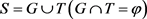 为群G的膨胀。则S是左
为群G的膨胀。则S是左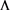 半群当且仅当对于G中单位元e,
半群当且仅当对于G中单位元e,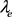 是S上的同余。
是S上的同余。
证明必要性显然成立。下面证明充分性。设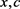 是S中的任意元素。若
是S中的任意元素。若 ,由S为群G的膨胀得
,由S为群G的膨胀得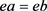 。由
。由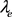 是S上的同余得
是S上的同余得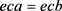 ,
,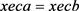 ,
,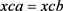 。因此
。因此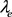 是同余。
是同余。
3. 循环群膨胀的性质
如果S是群G的膨胀,e是G的单位元,那么e是S的中心幂等元。交换群的膨胀是交换半群。特别地,循环群是交换群,循环群的膨胀也是交换半群,但是循环群的交并不一定是交换半群。
例3.1. 令半群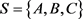 为
为 矩阵半群,其
矩阵半群,其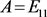 ,
,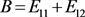 ,
,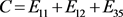 (
(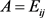 表示第i行第j列的元素1,其余元素全部为零的
表示第i行第j列的元素1,其余元素全部为零的 矩阵)。则由乘法运算有S的乘法表。
矩阵)。则由乘法运算有S的乘法表。
则S不是交换半群。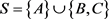 。
。 是循环群
是循环群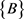 的膨胀。
的膨胀。
定理 3.2.设n为正整数,半群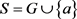 ,并且
,并且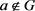 。G是由g生成的n阶循环群,e为G中单位元,S是G的膨胀。则对任意
。G是由g生成的n阶循环群,e为G中单位元,S是G的膨胀。则对任意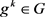 ,有
,有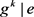 ,
,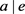 。
。
证明因为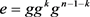 ,所以由命题1.9得
,所以由命题1.9得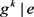 。由
。由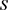 为群G的膨胀得
为群G的膨胀得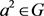 。于是有
。于是有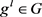 使得
使得 ,从而
,从而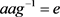 ,
,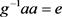 。故
。故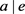 。
。
定理 3.3.设n为正整数,半群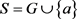 ,并且
,并且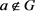 。G是由g生成的n阶循环群,e为G中单位元。则下列条件等价:
。G是由g生成的n阶循环群,e为G中单位元。则下列条件等价:
i) S是G的膨胀;
ii)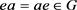 ,
,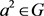 ;
;
iii)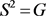 ,
, 。
。
证明 i)  ii) 因为S为循环群G的膨胀,所以存在
ii) 因为S为循环群G的膨胀,所以存在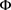 是S到G的膨胀映射。由
是S到G的膨胀映射。由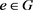 ,
,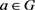 得
得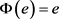 ,
,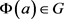 ,
,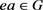 ,
,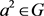 。于是
。于是 。同理
。同理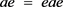 。因此
。因此 。
。
ii)  iii) 显然。
iii) 显然。
iii)  i) 由于
i) 由于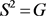 ,所以
,所以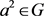 。任取
。任取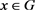 ,令
,令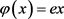 ,则知
,则知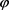 是S到G的膨胀映射,即S是G的膨胀。
是S到G的膨胀映射,即S是G的膨胀。
定理 3.4.设n为正整数,半群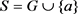 ,并且
,并且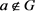 。G是由g生成的n阶循环群,e为G中单位元。如果有非负整数
。G是由g生成的n阶循环群,e为G中单位元。如果有非负整数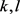 使得
使得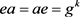 ,
, ,那么S是G的膨胀,并且对于任意
,那么S是G的膨胀,并且对于任意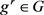 有
有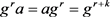 ,
,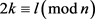 ,其中
,其中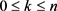 ,
,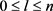 。
。
证明由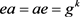 得
得
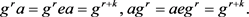
因此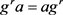 ,即S为交换半群。由定理3.3得S是G的膨胀。由于
,即S为交换半群。由定理3.3得S是G的膨胀。由于 ,
,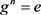 ,所以
,所以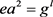 ,从而
,从而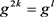 ,
,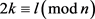 。
。
定理 3.5.设n为正整数,半群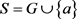 ,并且
,并且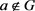 。G是由g生成的n阶循环群,e为G中单位元,S是G的膨胀。则
。G是由g生成的n阶循环群,e为G中单位元,S是G的膨胀。则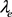 是S上的同余。
是S上的同余。
证明显然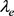 是S上的右同余。设
是S上的右同余。设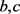 为S中元素,并且
为S中元素,并且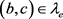 ,d是S中任意元素。则
,d是S中任意元素。则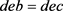 ,
,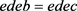 。由S是G的膨胀得
。由S是G的膨胀得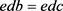 ,故
,故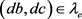 ,即
,即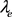 是S上的左同余。因此,
是S上的左同余。因此,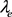 是S上的同余。
是S上的同余。
设n为正整数,半群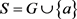 ,并且
,并且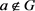 。S是n阶循环群G的膨胀。下面给出
。S是n阶循环群G的膨胀。下面给出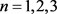 时G的乘法表(表1~6)。
时G的乘法表(表1~6)。
Table 1. Multiplication table of semigroup when, and
表1. ,
,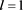 和
和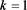 时
时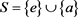 的乘法表
的乘法表
Table 2. Multiplication table of semigroup when, and
表2.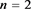 ,
,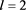 ,
,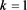 时半群
时半群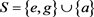 的乘法表
的乘法表
Table 3. Multiplication table of semigroup when, and
表3.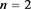 ,
,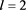 和
和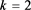 时半群
时半群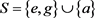 的乘法表
的乘法表
Table 4. Multiplication table of semigroup when, and
表4.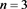 ,
,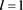 和
和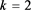 时半群
时半群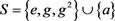 的乘法表
的乘法表
Table 5. Multiplication table of semigroup when, and
表5.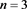 ,
,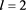 和
和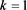 时半群
时半群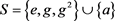 的乘法表
的乘法表
Table 6. Multiplication table of semigroup when, and
表6.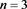 ,
,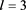 和
和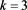 时半群
时半群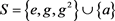 的乘法表
的乘法表
设半群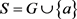 ,G是由g生成的n阶循环群,S是G的膨胀。下面给出S的乘法表(表7)。
,G是由g生成的n阶循环群,S是G的膨胀。下面给出S的乘法表(表7)。
Table 7. Multiplication table of semigroup
表7.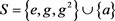 的乘法表
的乘法表
设半群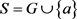 ,G是由g生成的n阶循环群,S是G的膨胀。下面给出
,G是由g生成的n阶循环群,S是G的膨胀。下面给出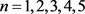 时l和k的取值表(表8)。
时l和k的取值表(表8)。
Table 8. Value table of n, l and k
表8. n,l和k的取值表
基金项目
本文由宁夏高等学校科研项目(NGY2017011)资助。
文章引用
杜 兰,龙品红. 有限循环群的膨胀
The Inflations of Finite Cyclic Groups[J]. 理论数学, 2018, 08(01): 113-119. http://dx.doi.org/10.12677/PM.2018.81014
参考文献 (References)
- 1. 郭聿琦, 任学明. E-理想拟正则半群[J]. 中国科学(A辑), 1989(5): 479-486.
- 2. 廖群英, 喻秉钧. 平移同态的正规带及其膨胀[J]. 四川师范大学学报(自然科学版), 1999, 22(2): 125-129.
- 3. Monzo, R.A.R. (2008) Further Results in Theory of Generalized Inflations of Semigroups. Semigroup Forum, 76, 540-560.
- 4. Putcha, M.S. and Weissglass, J. (1971) A Semilattice Decomposition into Semigroups Having at Most One Idempotent. Pacific Journal of Mathematics, 39, 225-228.
- 5. 张建新, 唐善桂. 强幂等元、强周期半群及正则半群[J]. 国防科技大学学报, 2000, 22(2): 115-116.
- 6. 高艳玲. 关于左-半群[J]. 青海师范大学学报(自然科学版), 1995(1): 9-12.
