Pure Mathematics
Vol.
09
No.
01
(
2019
), Article ID:
28694
,
8
pages
10.12677/PM.2019.91014
Using the Extend (G'/G) Expansion Method to Obtain the Exact Solution of the (3 + 1)-Dimensional Potential YTSF Equation
Houxu Mo, Yanfeng Guo, Pingli Zhu, Ganjie Liao
College of Science, Guangxi University of Science and Technology, Liuzhou Guangxi
Received: Jan. 4th, 2019; accepted: Jan. 22nd, 2019; published: Jan. 29th, 2019

ABSTRACT
Using the extend (G'/G)-expansion method and the new auxiliary equations, the new exact solutions of (3 + 1)-dimensional potential Yu-Toda-Sasa-Fukuyama (YTSF) equation are obtained on the basis of the homogeneous balance method. And some forms of exact solutions of (3 + 1)-dimensional potential (YTSF) equation are given. Furthermore, the corresponding figures are given.
Keywords:(G'/G)-Expansion Methods, YTSF Equation, Exact Solution
利用扩展的(G'/G)展开法求(3 + 1)维YSFY势方程的精确解
莫厚旭,郭艳凤,朱萍丽,廖干杰
广西科技大学,理学院,广西 柳州
收稿日期:2019年1月4日;录用日期:2019年1月22日;发布日期:2019年1月29日

摘 要
利用扩展的(G'/G)展开法和新的辅助方程,通过借助齐次平衡法确定相关次幂,求解(3 + 1)维Yu-Toda-Sasa-Fukuyama (YTSF)势方程的新精确解,得到了(3 + 1)维YTSF势方程的一些新的精确解的形式,并给出解的相应图形。
关键词 :扩展的(G'/G)展开法,YTSF势方程,精确解

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 前言
随着社会的进步,科技的发展,非线性偏微分方程在物理、数学等学科上的应用越来越广泛,因此也引起了许多数学家的关注。近年来,在许多学者的努力下,提出了许多求解非线性偏微分方程的精确解的方法,例如:Fourier变换 [1] ,三波法 [2] [3] [4] ,可变分离法 [5] 等方法来求解某类非线性偏微分方程的精确解。
本文主要考虑(3 + 1)维Yu-Toda-Sasa-Fukuyama (YTSF)势方程的新精确解。此方程为
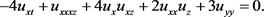 (1)
(1)
在1998年,Song-Ju Yu等人 [6] 将Bogoyavlenskii-Schiff方程 [7]
拓展为一个新的(3 + 1)维非线性演化方程
于是它被称为(3 + 1)维的Yu-Toda-Sasa-Fukuyama (YTSF)势方程,他们随后给出了该方程的行波解。为了方便研究,利用变换 把此方程化为它的潜在形式,也就是本文将要考虑的(3 + 1)维Yu-Toda-Sasa-Fukuyama (YTSF)势方程。
通过扩展的同宿测试法 [8] [9] ,可以获得(3 + 1)维Yu-Toda-Sasa-Fukuyama (YTSF)势方程 [10] 的精确纽结呼吸波解,利用auto-Backland [11] 变换和广义投影的Riccati [12] 方程方法可以得到关于(3 + 1)维YTSF势方程的一些类孤立波子解和非行波解。本文将利用扩展的 展开法 [13] 和新的辅助方程 [13]
(2)
来求解YTSF势方程的一些新精确解的形式。
2. 扩展的 展开法的概述
1) 对于一般的非线性偏微分方程
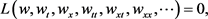 (3)
(3)
其中
是 及关于
的各阶导数的多项式。然后对(3)进行行波变换
及关于
的各阶导数的多项式。然后对(3)进行行波变换
(4)
为待定常数,将(4)代入(3)中,(3)就可化为
(5)
其中
2) 设方程(5)的拟解为
(6)
其中 , 中为待定常数, 可取 , 可通过齐次平衡法求出来,并且 满足以下非线性常微分方程
(7)
其中 为待定常数。
3) 将方程(6)和方程(7)代入方程(5)中,并将 中相同的指数幂的系数合并,令各次幂的系数为零,得到一个关于 , , 的代数方程组。
4) 利用maple软件求解代数方程组,确定待定常数之间的关系。
5) 通过文献 [13] ,得到5组关于 的表达式
a) 当 且 时,
(8)
b) 当 且 时,
(9)
c) 当 且 时,
(10)
d) 当 且 时,
(11)
e) 当 , 时,
(12)
3. Yu-Toda-Sasa-Fukuyama势方程的新精确解
对方程(1)引入变换(4) ,可将(1)化为方程
(13)
对方程(13)两边进行一次积分得
(14)
其中
为待定常数,由(6)可知
关于
的最高次幂为
,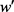 关于
的最高次幂为
,
关于
的最高次幂为
,由齐次平衡法得,最高阶导数线性项
和非线性项
进行平衡,则
,解得
。则(6)的表达式为
关于
的最高次幂为
,
关于
的最高次幂为
,由齐次平衡法得,最高阶导数线性项
和非线性项
进行平衡,则
,解得
。则(6)的表达式为
(15)
将(15)代入(14),得到3组解符合我们(3 + 1)维方程的系数关系
第一组:
第二组:
第三组:
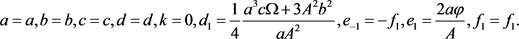
当第一、二、三组解满足 的条件时, 的表达式为
令 ( 为不为零的常数),利用maple软件画出部分解的图像,如下:(图1~图3)
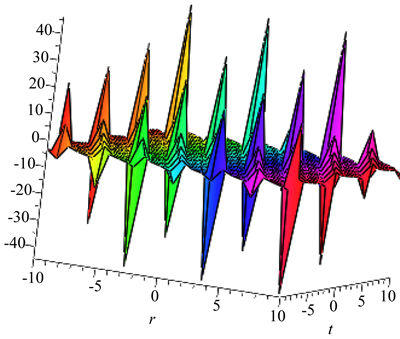
Figure 1. Triangle function solution schematic diagram
图1. 三角函数求解示意图

Figure 2. Rational partition solution schematic diagram
图2. 合理分区解示意图

Figure 3. Hyperbolic function solution schematic diagram
图3. 双曲函数求解示意图
4. 结论
本文通过引用文献 [13] 中扩展的 方法求解(3 + 1)维YTSF势方程的精确解,此方法是把原来 正次幂的形式扩展成 展正负次幂的形式,在此基础上引入新的辅助常微分方程(2)的解的不同形式。通过maple软件确定表达式中待定参数之间的关系,即当方程(2)系数 满足(8)~(12)的关系时,得到了非线性偏微分方程的(3 + 1)维YTSF势方程的新的负幂次形式的精确解,包括双曲函数解、有理分式解和三角函数解的形式,并且此方法还可以用于求解其它非线性偏微分方程。三角函数具有周期性,三角函数解的图像如图1;有理分式的图像如图2所示,由图可以看出此图为中心对称图形;双曲函数是一种类似于三角函数的函数,具有三角函数的一些性质,双曲函数解的图像如图3,是中心对称图像。同时也希望能为大家拓宽解决此类问题的方法。
文章引用
莫厚旭,郭艳凤,朱萍丽,廖干杰. 利用扩展的(G'/G)展开法求(3 + 1)维YSFY势方程的精确解
Using the Extend (G'/G) Expansion Method to Obtain the Exact Solution of the (3 + 1)-Dimensional Potential YTSF Equation[J]. 理论数学, 2019, 09(01): 111-118. https://doi.org/10.12677/PM.2019.91014
参考文献
- 1. 王元明. 数学物理方程与特殊函数(第三版) [M]. 北京: 高等教育出版社, 2004.
- 2. 傅海明, 戴正德. (2+1)维广义KdV方程的周期孤波解[J]. 平顶山学院学报, 2013, 28(5): 35-38.
- 3. 刘建国, 曾志芳. 变系数Sine-Gordon 方程的Bäcklund变换和新的精确解[J]. 系统科学与数学, 2014, 34(6): 763-768.
- 4. 傅海明, 戴正德. (2+1)维Nizhnik-Novikov方程的周期孤波解[J]. 江苏师范学报(自然科学版), 2016, 34(2): 33-36.
- 5. Kongl, Q. and Dai, C.Q. (2015) Some Discussions about Variable Separation of Nonlinear Models Using Riccati Equation Expansion Method. Nonlinear Dynamics, 81, 1553-1561.
https://doi.org/10.1007/s11071-015-2089-y - 6. Yu, S.J., Toda, K., Sasa, N. and Fukuyama, T. (1998) N-Solitions to the Bo-goyavlenskii-Schiff Equation and Aquest for the Solition in (3+1)-Dimensions. Journal of Physics A, 31, 3337.
https://doi.org/10.1088/0305-4470/31/14/018 - 7. Schff, J. and Painleve, T. (1992) Their Asymptotics and Physical Applica-tions. Plenum, New York.
- 8. Vladimirov, V.A. and Maczka, C. (2007) Exact Solutions of Generalized Burgers Equation, De-scribing Travelling Fronts and Their Interaction. Reports on Mathematical Physics, 60, 317-328.
https://doi.org/10.1016/S0034-4877(07)80142-X - 9. Darvishi, M.T., Najafi, M., Kavitha, L. and Venkatesh, M. (2012) Stair and Step Solition Solutions of the Integrable (2+1) and (3+1)-Dimensional Boiti-Leon-Manna-Pempinelli Equations. Communications in Theoretical Physics, 58, 785-794.
https://doi.org/10.1088/0253-6102/58/6/01 - 10. Tan, W. and Dai, Z.D. (2016) Dynamics of Kinky Wave for (3+1)- Dimensional Potential Yu-Toda-Sasa-Fukuyama. Nonlinear Dynamics, 85, 817-823.
https://doi.org/10.1007/s11071-016-2725-1 - 11. Yun, Z. (2003) New Families of Nontravelling Wave Solutions to a New (3+1)-Dimensional Potential-YTSF Equation. Physics Letters A, 318, 78-83.
https://doi.org/10.1016/j.physleta.2003.08.073 - 12. Zhang, T., Xuan, H.N., Zhang, D.F. and Wang, C.J. (2007) Nontraveling Wave Solutions to a (3+1) Dimensional Potential YTSF Equation and a Simplified Model for Reacting Mixtures. Chaos, Solitions Fractals, 34, 1006-1013.
https://doi.org/10.1016/j.chaos.2006.04.005 - 13. Hasibun, N. and Farah, A. (2014) New Generalized and Improved (G'/G)-Expansion Method for Nonlinear Evolution Equations in Mathematical Physic. Journal of the Egyptian Mathematical Society, 22, 390-395.
https://doi.org/10.1016/j.joems.2013.11.008