Pure Mathematics
Vol.
10
No.
04
(
2020
), Article ID:
35207
,
6
pages
10.12677/PM.2020.104045
Ranks of Compact Operator Ideals on Hilbert C*-Modules
Xin Wang
School of Mathematical Sciences, Ocean University of China, Qingdao Shandong
Received: Mar. 27th, 2020; accepted: Apr. 16th, 2020; published: Apr. 23rd, 2020

ABSTRACT
Let A be a C*-algebra and E be a Hilbert C*-module over A. In this paper, the completely positive rank and homogeneous rank of the compact operator ideal K(E) on E are studied, and it is proved that the ranks of K(E) do not exceed n when the two ranks of A do not exceed n.
Keywords:Hilbert C*-Module, Compact Operator Ideal, Completely Positive Rank, Homogeneous Rank

Hilbert C*-模上紧算子理想的秩
王欣
中国海洋大学数学科学学院,山东 青岛
收稿日期:2020年3月27日;录用日期:2020年4月16日;发布日期:2020年4月23日

摘 要
设A为C*-代数,E为A上的Hilbert C*-模。本文研究了E上紧算子理想 的完全正秩与齐次秩,证明了当A的这两种秩不超过n时, 的秩亦不超过n。
关键词 :Hilbert C*-模,紧算子理想,完全正秩,齐次秩

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Hilbert C*-模最初是1953年I. Kaplansky [1] 在交换单位代数上提出的,在20世纪70年代,该理论被拓展到非交换C*-代数。非交换维数是覆盖维数在非交换C*-代数的推广,21世纪初W. Winter提出了完全正秩 [2] 和齐次秩 [3],有力地推动了C*-代数的分类。
在已有理论的基础上,本文研究了Hilbert C*-模上紧算子理想的保持完全正秩和齐次秩的条件,证明了当A的这两种秩不超过n时, 的秩亦不超过n。
2. 预备知识
定义1.1 [2] 设A是C*-代数,F是有限维C*-代数,对 如果 是相互正交的最小投影,则称 是基本集。
定义1.2 [4] 设A,B是C*-代数, 是线性映射且满足对任意的正元 , 也是正元,则称 是正线性映射,若对任意的n, , 都是正线性映射,则称 是完全正线性映射,简称完全正映射。
定义1.3 [2] 设A是C*-代数,F是有限维C*-代数。对完全正映射 ,如果n是满足对F中的任意基本集 都存在 使得 的最小整数,则称 的严格阶等于n。
定义1.4 [2] 设A是C*-代数,如果对任意 ,,都存在对 的关于 的完全正逼近 使得 的严格阶不超过n,则称A的完全正秩小于等于n,记作 。如果n是使得 成立的最小整数,则称 。
定义1.5 [3] 设A是C*-代数, 是完全正映射收缩, 为典范单位嵌入。如果任给 ,,则称 是分段齐次的,如果 是分段齐次的,且 ,则称 是严格阶为n的分段齐次。
定义1.6 [3] 设A是C*-代数,如果对任意
,,都存在对
的关于 的完全正逼近
的完全正逼近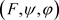 ,使得
,使得 是严格阶不超过n的分段齐次,则称A的齐次秩不超过n,记作
是严格阶不超过n的分段齐次,则称A的齐次秩不超过n,记作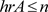 。
。
3. 完全正秩
引理2.1 设A为单的C*-代数,H为可分的Hilbert空间,则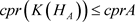 。
。
证明:因为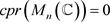 ,由 [2] 命题2.11,
,由 [2] 命题2.11,
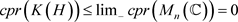 .
.
因为A是单的,由 [3] 定理3.2.4,
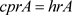 ,
,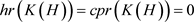 .
.
由 [3] 命题3.1.4,得
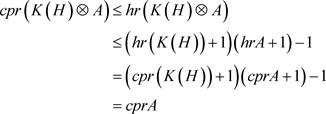 .
.
即
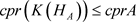 .
.
引理2.2 设A为C*-代数,令 。若任给
。若任给 ,都有
,都有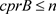 ,则
,则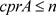 。
。
证明:任给有限集 ,
,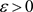 ,令B为F生成的子代数,由
,令B为F生成的子代数,由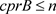 ,对
,对 ,
,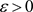 ,存在对F的关于
,存在对F的关于 的完全正逼近
的完全正逼近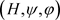 使得
使得
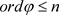 .
.
对 ,由 [5] 定理7.5,存在完全正映射收缩
,由 [5] 定理7.5,存在完全正映射收缩 ,使得
,使得
 ,
,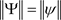 .
.
令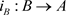 为包含映射,
为包含映射,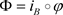 。则
。则 为对F的关于
为对F的关于 的完全正逼近,并且
的完全正逼近,并且 。
。
综上所述, 。
。
引理2.3 设A,F为C*-代数, ,
,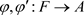 为完全正映射,且满足任给
为完全正映射,且满足任给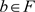 ,
, 。若
。若 且满足
且满足 ,则
,则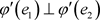 。
。
证明:令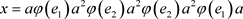 ,则
,则 。而
。而
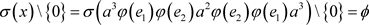 ,
,
所以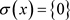 ,得
,得
 ,
,
因此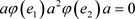 ,即
,即
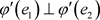 .
.
定理2.4 设A是C*-代数,B为A的遗传子代数,则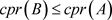 。
。
证明:设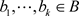 ,存在关于
,存在关于 的完全正逼近
的完全正逼近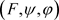 使得
使得
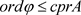 .
.
利用近似单位,可以找到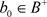 ,
, 使得
使得
任给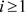 ,
,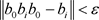 .
.
令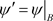 ,
, ,
,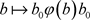 ,则
,则
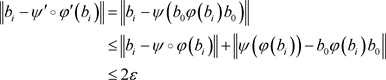 .
.
不妨设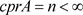 ,则对F的每个基本集
,则对F的每个基本集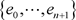 ,存在
,存在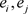 使得
使得
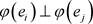 ,
,
由引理2.3,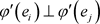 。因此
。因此
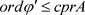 .
.
当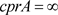 时,显然有
时,显然有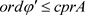 。
。
定理2.5设A为单的C*-代数,E为Hilbert-A模。若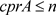 ,则
,则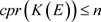 。
。
证明:由引理2.1,有
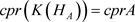 ,
,
E可数生成时, ,所以
,所以
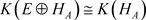 .
.
因为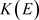 为
为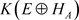 的遗传子代数,由引理2.2得
的遗传子代数,由引理2.2得
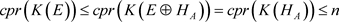 .
.
E为任意Hilbert-A模时:
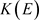 可分时,设
可分时,设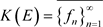 ,由
,由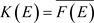 ,存在
,存在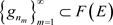 ,使得
,使得
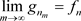 ,
,
设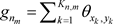 ,
,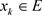 ,
,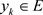 。令
。令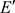 为
为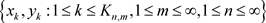 生成的Hilbert-A模。由
生成的Hilbert-A模。由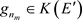 ,得
,得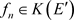 ,所以
,所以 ,又有
,又有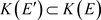 ,所以
,所以 。由
。由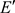 为可数生成,得
为可数生成,得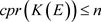 。
。
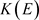 不可分时,
不可分时,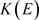 的所有有限生成子代数可分,所以其完全正秩
的所有有限生成子代数可分,所以其完全正秩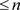 ,由引理2.2,
,由引理2.2,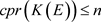 。
。
4. 齐次秩
引理3.1 设A为C*-代数,令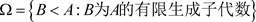 。若任给
。若任给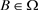 ,都有
,都有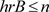 ,则
,则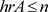 。
。
证明:任给有限集 ,
,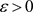 ,令B为F生成的子代数,由
,令B为F生成的子代数,由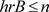 ,对
,对 ,
,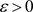 ,存在对F的关于
,存在对F的关于 的完全正逼近
的完全正逼近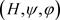 使得
使得
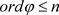 .
.
对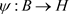 ,由 [5] 定理7.5,存在完全正映射收缩
,由 [5] 定理7.5,存在完全正映射收缩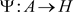 ,使得
,使得
 ,
,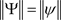 .
.
令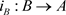 为包含映射,
为包含映射,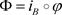 。则
。则 为对F的关于
为对F的关于 的分段齐次的完全正逼近,并且
的分段齐次的完全正逼近,并且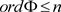 。
。
综上所述,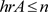 。
。
引理3.2设A,F为C*-代数,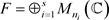 ,
, ,
,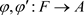 为完全正映射,且满足
为完全正映射,且满足 ,
,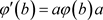 。设
。设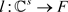 为典范单位嵌入,若
为典范单位嵌入,若 为正元,且满足
为正元,且满足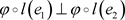 ,则
,则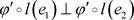 。
。
证明:令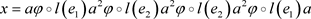 ,则
,则 。而
。而
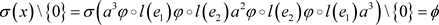 ,
,
所以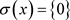 。得
。得
 ,
,
因此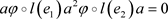 ,即
,即
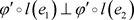 .
.
定理3.3 设A是C*-代数,B为A的遗传子代数,则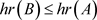 。
。
证明:设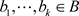 ,存在关于
,存在关于 的完全正逼近
的完全正逼近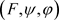 ,
,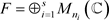 ,使得
,使得
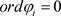 ,
,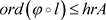 .
.
其中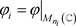 ,
,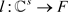 为典范单位嵌入。利用近似单位,可以找到
为典范单位嵌入。利用近似单位,可以找到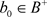 ,
, 使得
使得
任给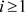 ,
,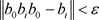 .
.
令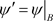 ,
,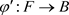 ,
,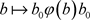 ,则
,则
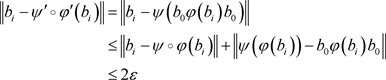 .
.
设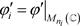 ,则由引理2.3,
,则由引理2.3,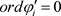 。不妨设
。不妨设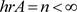 ,则对
,则对 的每个基本集
的每个基本集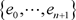 ,存在
,存在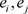 使得
使得
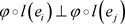 ,
,
由引理3.2,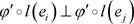 。因此
。因此
 .
.
当 时,显然有
时,显然有 。
。
综上所述,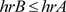 。
。
定理3.4设A为C*-代数,E为Hilbert-A模。若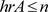 ,则
,则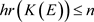 。
。
证明:由 [2] 命题3.1.4,有
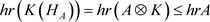 .
.
E可数生成时,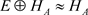 ,所以
,所以
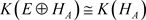 .
.
因为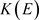 为
为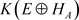 的遗传子代数,由引理3.3得
的遗传子代数,由引理3.3得
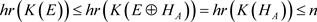 .
.
E为任意Hilbert-A模时:
 可分时,设
可分时,设 ,由
,由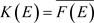 ,存在
,存在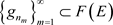 ,使得
,使得
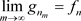 .
.
设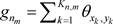 ,
,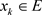 ,
,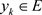 。令
。令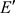 为
为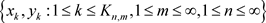 生成的Hilber-A模。由
生成的Hilber-A模。由 ,得
,得 。所以
。所以 ,又有
,又有 ,所以
,所以 。由
。由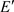 为可数生成,得
为可数生成,得 。
。
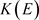 不可分时,
不可分时, 的所有有限生成子代数可分,所以其齐次秩
的所有有限生成子代数可分,所以其齐次秩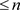 ,由引理3.1,
,由引理3.1,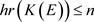 。
。
文章引用
王 欣. Hilbert C*-模上紧算子理想的秩
Ranks of Compact Operator Ideals on Hilbert C*-Modules[J]. 理论数学, 2020, 10(04): 356-361. https://doi.org/10.12677/PM.2020.104045
参考文献
- 1. Kaplansky, I. (1953) Modules over Operator Algebras. American Journal of Mathematics, 75, 839-858. https://doi.org/10.2307/2372552
- 2. Winter, W. (2003) Covering Dimension for Nuclear C*-Algebras. Journal of Functional Analysis, 199, 535-556. https://doi.org/10.1016/S0022-1236(02)00109-X
- 3. Winter, W. (2009) Covering Dimension for Nuclear C*-Algebras II. American Mathematical Society, 361, 4143-4167. https://doi.org/10.1090/S0002-9947-09-04602-9
- 4. Lin, H. (2001) An Introduction to the Classification of Amenable C*-Algebras. World Scientific, New Jersey, London, Singapore, Hong Kong. https://doi.org/10.1142/4751
- 5. Paulsen, V. (2002) Completely Bounded Maps and Operator Algebras. Cam-bridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511546631