Pure Mathematics
Vol.
10
No.
05
(
2020
), Article ID:
35615
,
10
pages
10.12677/PM.2020.105062
Two Difference Schemes for Nonlinear Wave Equations with Delay
Jingliang Chen, Dingwen Deng
College of Mathematics and Information Science, Nanchang Hangkong University, Nanchang Jiangxi
Received: Apr. 20th, 2020; accepted: May 11th, 2020; published: May 18th, 2020

ABSTRACT
This study is concerned with numerical solutions of delayed wave equations by explicit finite difference methods. By using the discrete energy method, it is shown that both of them are temporally and spatially second-order convergent in maximum norm. Numerical findings confirm the accuracy and efficiency of the algorithms.
Keywords:Nonlinear Wave Equation with Delay, Explicit Difference Methods, Convergence

非线性延迟波动方程的两类差分格式
陈景良,邓定文
南昌航空大学,数学与信息科学学院,江西 南昌
收稿日期:2020年4月20日;录用日期:2020年5月11日;发布日期:2020年5月18日

摘 要
本文对一类非线性延迟波动方程建立了两类显式差分格式。运用能量法,证明了在最大模意义下它们在时、空方向上均有二阶收敛率。数值结果验证了算法的精度和有效性。
关键词 :非线性延迟波动方程,显式差分方法,收敛性

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在许多实际问题中,需要利用系统过去时刻的状态,因而提出了延迟微分方程模型。延迟微分方程也称时滞微分方程,属于泛函微分方程。它们在图形处理、计算机科学、生态、经济、物理、人口动力学、生物医学等各个科学领域有着广泛的应用。正因为延迟微分方程具有很强的应用背景,它们的研究受到了人们的长期关注(见文献 [1] - [6] 及其参考文献)。与经典微分方程相比,它们的解不仅与当前的状态有关,还受过去一段时间的影响。延迟项的存在不仅给理论研究带来困难,也给数值研究带来了挑战。近些年来,在延迟抛物方程的数值研究方面,已有不少成果。文献 [2] [3] 研究了非线性延迟抛物方程的紧致差分法及其理论。文献 [4] 研究了变系数时滞反应扩散方程的紧致差分法。文献 [5] 研究了时间分数阶变系数时滞抛物方程的紧致差分法及其收敛性。然而,人们对延迟双曲方程的数值研究关注不多。文献 [6] 研究了一维时滞波动的紧致差分法及其Richardson外推法。
显式差分法虽然是条件稳定的,但是由于不需要解线性方程组,程序易于实现、计算量小等优势受到人们的青睐。特别对二阶波动来说,稳定条件是可接受的,并不苛刻。此外,为了克服抛物方程显式差分法的稳定条件的限制,提出无条件稳定的 Du Fort-Frankel格式。本文推广经典波动方程的显式差分格式,对如下非线性延迟波动方程
,,, (1a)
,,, (1b)
,,, (1c)
建立两类差分格式及其算法理论。
2. 差分格式
2.1. 记号
为了用差分方法求解问题(1a)~(1c),我们对
做剖分。将空间区间
剖分m等份(m为整数),记空间步长
(
)。在时间方向上,采用限制性网格时间步长
(
),
均为整数,记
,,,, 均为整数。在结点
处的精确解和数值解分别记为
,。记网格剖分区域
,定义网格函数空间
,对任意
,引用差分算子,内积和范数如下
,,,
,,,
,,.
2.2. 两类差分格式的建立
由泰勒展式可知
,.
从而,在结点
处用差分算子
, 离散
, 可得
,,, (2)
其中,
,,. (3)
用
代替
,略去小量项
,得到第一个差分格式
,,, (4a)
,,, (4b)
,,. (4c)
记网格步长比
,对差分算子
做如下处理
. (5)
将(5)式代入(2)式中得
,,, (6)
其中
,,. (7)
舍去(6)式的
项,用
代替
,便得到了第二个差分格式
,,, (8a)
,,, (8b)
,,. (8c)
2.3. 差分格式的收敛性分析
为研究上述两个差分格式的收敛性,我们现引入两个引理。
引理2.1 [7] 设
,则有下列不等式成立
,,
,.
引理2.2 [8] 设A和B是非负常数,
是非负序列且满足
, 则
此外,若
,则
。其中
足够小,使得
。
另外,存在常数
,使得
,,, (9)
,,, (10)
成立。
假设
满足局部Lipschitz条件。设u,v为问题方程(1a)~(1c)的真解,且存在正常数
,,当
,(
),函数
满足如下等式
(11)
成立,其中
为Lipschitz常数。
定理2.1 设问题(1a)~(1c)在节点
的精确解为
, 为差分格式 (4a)~(4c)的解。记
。当
时且步长满足以下条件
,,
则有,当
时,下列估计
,, (12a)
,, (12b)
成立。此处
。
证明 将方程(2)式与(4a)式相减,得到误差方程
,,, (13a)
,,, (13b)
, 或
,. (13c)
当
时,
,显然(12a)式与(12b)式成立。
假设当
时,(12a)式成立,则当步长满足
, 时,应用引理2.1可知
,.
记
为
, 为
。运用不等式
和(11) 式可得
,. (14)
记
。当
时,对(13a)式两端同时与
做內积,运用引理2.1得
. (15)
运用等式
和引理2.1,可得
. (16)
由(16)式可得
,. (17)
由不等式
和不等式
可得
. (18)
. (19)
另外,由
有
,. (20)
将上式两端平方后,运用均值不等式
得
,. (21)
在(21)式两端乘以
并对i求和,结合(17)式可得
,. (22)
将估计项(18)~(19)代入式子(15)后,运用(22)式和引理2.1得
. (23)
将上式中的k用p替换,两端同时乘以
,并对p从−1到k求和可得
. (24)
当
时,在(24)式中运用引理2.2可推得
,. (25)
在(25)式中令
,运用(22)式和引理2.1,可得
,.
故当
时假设依然成立。由数学归纳法可知定理成立。
定理2.2 设问题(1a)~(1c)在节点
的精确解为
,原问题格式(8a)~(8c)的数值解为
。记
。当步长满足
,,, (26)
时,则在
的条件下,有
,, (27a)
,, (27b)
成立,其中
。
证明 将方程(6)式与(8a)式相减,得到误差方程组
,, (28a)
,,, (28b)
, 或
,. (28c)
或
,. (28c)
当
时,
,显然(27a)式与(27b)式成立。
假设当
时,(27a)式成立,则当步长满足(26)时,应用引理2.1可知
,.
从而,运用(11)式可得
,.(29)
记
,对(28a)式两端与
做內积,运用离散的格林公式得
. (30)
借用(16)式的处理技巧,不难得到
. (31)
由(31)式可得
,. (32)
应用不等式
和不等式
可得
(33)
. (34)
运用与(22)式相同的分析方法可得
,. (35)
将估计项(33)~(35)代入式子(30)中,运用(35)式和引理2.1得
. (36)
将上式中的k用p替换,两端同时乘以
,并对p从0到k求和可得
. (37)
当
时,在(37)式运用引理2.2,我们有
,. (38)
在(38)式中令
时,应用(34)式有
,.
从而,当
时假设依然成立。由数学归纳法知定理2.2成立。
3. 数值实验
算例 应用格式(4a)~(4c)和(8a)~(8c)计算如下非线性初边值问题:
,,
,,
,,,
其中,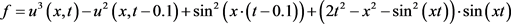 。问题的真解为
。表1为差分格式(4a)~(4c)在
时取不同步长时数值解得到的最大误差。表2为格式(8a)~(8c)在
时取不同步长时数值解得到的最大误差,其中,CPU为程序运行时间,
,。
。问题的真解为
。表1为差分格式(4a)~(4c)在
时取不同步长时数值解得到的最大误差。表2为格式(8a)~(8c)在
时取不同步长时数值解得到的最大误差,其中,CPU为程序运行时间,
,。

Table 1. FDM (4a)~(4c) maximum error for numerical solution
表1. 差分方法(4a)~(4c)在最大范数意义下数值解的误差

Table 2. FDM (8a)~(8c) maximum error for numerical solution
表2. 差分方法(8a)~(8c)在最大范数意义下数值解的误差
数值结果表明两类显式差分格式在时空方向具有二阶精度。格式(4a)~(4c)的计算效果更好一些。
4. 结论
本文受经典波动方程的显式差分法和抛物方程的Du Fort-Frankel差分法的启发,对非线性延迟波动方程问题建立了两类显式差分法。运用能量法,我们证明了它们在时、空方向上均有二阶收敛性。数值结果验证了理论结果的正确性。
基金项目
国家自然科学基金项目(No. 11861047)。
文章引用
陈景良,邓定文. 非线性延迟波动方程的两类差分格式
Two Difference Schemes for Nonlinear Wave Equations with Delay[J]. 理论数学, 2020, 10(05): 508-517. https://doi.org/10.12677/PM.2020.105062
参考文献
- 1. 熊君, 李俊民, 等. 一阶双曲型偏微分方程的模糊边界控制[J]. 数学物理学报, 2017, 37(3): 469-477.
- 2. 张在斌, 孙志忠. 一类非线性延迟抛物偏微分方程的Crank-Nicolson型差分格式[J]. 数值计算与计算机应用, 2010, 31(2): 131-140.
- 3. 池永日. 一类高精度非线性延迟抛物偏微分方程的紧差分格式[J]. 延边大学学报(自然科学版), 2010, 36(4): 287-290.
- 4. Xie, J., Deng, D. and Zheng, H. (2017) A Compact Difference Scheme for One-Dimensional Nonlinear Delay Reaction-Diffusion Equations with Variable Coefficient. IAENG International Journal of Applied Mathematics, 47, 14-19.
- 5. Xie, J., Deng, D. and Zheng, H. (2017) Fourth-Order Difference Solv-ers for Nonlinear Delayed Fractional Sub-Diffusion Equations with Variable Coefficients. International Journal of Modelling and Simulation, 37, 241-251. https://doi.org/10.1080/02286203.2017.1358133
- 6. 张启峰, 张诚坚, 邓定文. 求解非线性时滞双曲型偏微分方程的紧致差分方法及Richardson外推算法[J]. 数值计算与计算机应用, 2013, 34(3): 167-176.
- 7. 孙志忠. 偏微分方程数数值解法[M]. 北京: 科学出版社, 2012: 110-171.
- 8. Deng, D. (2018) Unified Compact ADI Methods for Solving Nonlinear Viscous and Nonviscous Wave Equations, Chinese Journal of Physics, 56, 2897-2915. https://doi.org/10.1016/j.cjph.2018.09.025






 或
,. (28c)
或
,. (28c)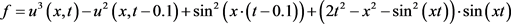 。问题的真解为
。表1为差分格式(4a)~(4c)在
时取不同步长时数值解得到的最大误差。表2为格式(8a)~(8c)在
时取不同步长时数值解得到的最大误差,其中,CPU为程序运行时间,
,。
。问题的真解为
。表1为差分格式(4a)~(4c)在
时取不同步长时数值解得到的最大误差。表2为格式(8a)~(8c)在
时取不同步长时数值解得到的最大误差,其中,CPU为程序运行时间,
,。