Pure Mathematics
Vol.
12
No.
01
(
2022
), Article ID:
48115
,
6
pages
10.12677/PM.2022.121014
一类传递置换群的极小基
陈媛媛
云南师范大学数学系,云南 昆明
收稿日期:2021年12月7日;录用日期:2022年1月13日;发布日期:2022年1月20日

摘要
群G作用在有限集合 上, , 称为G在 上的逐点稳定子。若 ,则称 为G群的基。若 是使得 成立的最小集合,则称 为群G的极小基。本文计算出对称群 与 的圈积 以及它的子群 , 在某种非本原作用下的极小基。
关键词
对称群,圈积,非本原作用,极小基

Minimal Bases of a Class of Transitive Permutation Groups
Yuanyuan Chen
School of Mathematics, Yunnan Normal University, Kunming Yunnan
Received: Dec. 7th, 2021; accepted: Jan. 13th, 2022; published: Jan. 20th, 2022

ABSTRACT
A group G acting on a finite set ,, is called a pointwise stabilizer on G. If , is called the basis of group G. If is the smallest set that makes true, then is called the minimal basis of group G. In this paper, the wreath product of symmetric groups and , the minimal basis of its subgroups and under some imprimitive action are calculated.
Keywords:Symmetric Group, Cycle Product, Imprimitive Action, Minimal Basis

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
基是研究向量空间和线性变换的一个非常重要和有用的工具。尤其在线性变换中,每一个线性变换完全取决于它在基上的作用。类似的,在研究置换群的过程中,基也是有用的工具。设G作用在集合 上, 的子集 被称为G的基,若满足 ;换句话说,在群G中有且仅有单位元能稳定 中的所有元素。在Dixon的经典著作 [1] 中给出了基的一些相关命题。
有限本原群的研究已经有了一些成果,具体参见Cameron (1981) [2] 和Praeger (1990) [3]。对于极小基的研究,Burness在 [4] 中给出了点稳定子属于S-collection的有限典型群的base sizes,他对有限散在单群的base sizes也进行了讨论,具体参考 [5]。Fawcett,Praeger在 [6] 中给出了非本原线性群的base sizes。在 [7] 中,Libeck对本原置换群的base sizes进行讨论。而本文主要利用圈积构造一些传递置换群,确定它们在某种非本原作用下的极小基和base sizes。
2. 预备知识
本节主要给出一些本文中要用到的基本概念及结果。
定义2.1 [1] 非空集合 到自身的一个双射,称为 的一个置换。 中全体置换构成的群,称为 上的对称群,记作 。
定义2.2 [1] 设 是一个非空集合,其中的元素称为一个点,群G在 上的一个作用是指G到 上的一个同态,即:
1) ,,其中1代表G中的单位元;
2) ,,。
定义2.3 [8] 设 为两个抽象群。 是同态映射,则N与F的半直积G为:
,
运算为 。
定义2.4 [8] 设G是群,H是有限集合 上的置换群 ,设N是n个G的直积: ,对于任意 ,映射 是N的一个自同构:
可作N与H的半直积 ,叫做G和H的圈积,记作 。
.
定义2.5 [8] 群G作用在有限集合 上, , 称为G在 上的逐点稳定子。若 ,则称 为群G的基。若 是使得 成立的最小集合,则称 为群G的极小基。
3. 传递置换群在非本原作用下的极小基
定理3.1 设 , 对称群 与 的圈积 非本原作用在 个点上的极小基形如:
,
其中 为集合 中任意 个元素, 。
证明:令 ,,,,
设 ,故 ,群G在集合 的非本原作用如下:
下面考虑逐点稳定子 时, 中有哪些元素。
令 ,,,,则:
故
因为 ,所以要使 ,则K至少要稳定 个点,即 ,故:
,
所以群 非本原作用在 上的极小基形如:
,.
定理3.2:设 ,当r为偶数时,二面体群 与对称群 的圈积 非本原作用在 个点上的极小基形如 ,其中 ,。
当r为奇数时,极小基形如 ,其中任意 ,。
证明:令 ,
设 ,则 。
群G在集合 上的作用同定理3.1,现在考虑逐点稳定子 时, 中有哪些元素。
首先考虑二面体群 的点稳定子群:
我们知道二面体群的点稳定子 ,其中x为二阶元,下面考虑什么时候二面体群的点稳定子为1。
情况1:r为偶数时, 。
那么此时由二面体群的生成元可知当 时, 。所以当r为偶数时,使得逐点稳定子 的最小集合为:
,其中 。
即当r为偶数时, 非本原作用在 上极小基形如 ,。
例如:
当 时, ,二面体群 ,如下图所示:
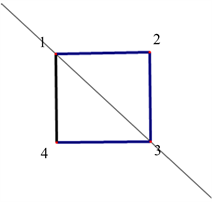
稳定点1,就要稳定点3,故 中稳定一个点的只有单位元与一个二阶元,即 ,,故有:
,
当 时, ,二面体群 ,如下图所示:
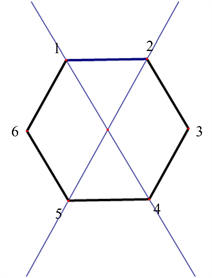
则有 ,,
,,
情况2:当r为奇数时,二面体群:
此时稳定 中任意一个元素的也只有单位元与一个二阶元,故可知:
其中 ,所以当r为奇数时, 非本原作用在 上极小基形如 ,其中 ,。
定理3.3:设 ,循环群 与对称群 的圈积 ,非本原作用在 个点上的极小基形如 ,其中任意 ,。
证明:令 ,
,
G在集合 上的作用同以上两个定理,现在同样考虑逐点稳定子 时, 中有哪些元素。
因为 本原正则作用在 上,故任意 有 ,则要使逐点稳定子 ,需要稳定 这r个点,其中任意 。
故群 非本原作用在 上的极小基 ,任意 ,且 。
文章引用
陈媛媛. 一类传递置换群的极小基
Minimal Bases of a Class of Transitive Permutation Groups[J]. 理论数学, 2022, 12(01): 103-108. https://doi.org/10.12677/PM.2022.121014
参考文献
- 1. Dixon, J.D. and Mortimer, B. (1996) Permutation Groups. In: Graduate Text in Mathematic, Springer-Verlag, Berlin. https://doi.org/10.1007/978-1-4612-0731-3
- 2. Cameron, P.J. (1981) Finite Permutation Groups and Finite Sim-ple Groups. Bulletin of the London Mathematical Society, 13, 1-22. https://doi.org/10.1112/blms/13.1.1
- 3. Praeger, C.E. (1990) Finite Permutation Groups: A Survey, Groups-Canberra. In: Lecture Notes in Mathematics, Springer-Verlag, Berlin, Vol. 1456, 63-84. https://doi.org/10.1007/BFb0100731
- 4. Burness, T.C., Guralnick, R.M. and Saxl, J. (2014) Base Sizes for S-Actions of Finite Classical Groups. Israel Journal of Mathematics, 199, 711-756. https://doi.org/10.1007/s11856-013-0059-y
- 5. Burness, T.C., O’Brien, E.A. and Wilson, R.A. (2010) Base Sizes for Sporadic Simple Groups. Israel Journal of Mathematics, 177, 307-333. https://doi.org/10.1007/s11856-010-0048-3
- 6. Fawcett, J.B. and Praeger, C.E. (2016) Base Sizes of Imprimitive Linear Groups and Orbits of General Linear Groups on Spanning Tuples. Archiv der Mathematik, 106, 305-314. https://doi.org/10.1007/s00013-016-0890-6
- 7. Liebeck, M.W. (1984) On Minimal Degrees and Base Sizes of Primitive Permutation Groups. Archiv der Mathematik, 43, 11-15. https://doi.org/10.1007/BF01193603
- 8. 徐明耀. 有限群导引(上册) [M]. 北京: 科学出版社, 2001.