Computer Science and Application
Vol.
12
No.
02
(
2022
), Article ID:
48848
,
13
pages
10.12677/CSA.2022.122040
基于T-S模糊模型的冠状动脉时滞系统 同步研究
曹秋霞
天津工业大学计算机科学与技术学院,天津
收稿日期:2022年1月18日;录用日期:2022年2月15日;发布日期:2022年2月22日

摘要
冠状动脉是给心脏供血的肌型血管,负责将氧气和营养物质输送到心脏血管,一旦血管阻塞和痉挛,会导致心血管以及血管痉挛等心脑血管疾病。为了治疗心脑血管疾病,了解冠状动脉血管痉挛的发病原理,实现冠状动脉系统的混沌同步是非常重要的。在实际工作中,冠状动脉系统的数学模型是难以精确构造的,而Takagi-Sugeno (T-S)模糊模型可以以任意精度逼近复杂的非线性系统,本文基于T-S模糊模型研究了冠状动脉系统的同步问题。本文考虑时滞对系统的影响,构造冠状动脉数学模型,结合Wirtinger积分不等式和一种新的二重积分不等式处理求导后的一重积分和二重积分,降低系统保守性,并基于并行分布式补偿方案,设计状态反馈控制器,有效实现了系统的同步。最后,通过仿真实例实现了本文方法的有效性。
关键词
冠状动脉系统,时变时滞,T-S模糊模型,积分不等式,混沌同步

Synchronization Study for Coronary Artery Time-Delay Systems Based on T-S Fuzzy Model
Qiuxia Cao
School of Computer Science and Technology, Tiangong University, Tianjin
Received: Jan. 18th, 2022; accepted: Feb. 15th, 2022; published: Feb. 22nd, 2022

ABSTRACT
Coronary arteries are muscular blood vessels that supply blood to the heart and are responsible for transporting oxygen and nutrients to the heart vessels. Once the blood vessels are blocked and spasm, it will lead to cardiovascular and cerebrovascular diseases such as cardiovascular and vasospasm. In order to treat cardiovascular and cerebrovascular diseases, it is very important to understand the pathogenesis of coronary vasospasm and realize the chaotic synchronization of the coronary systems. In practice, the mathematical model of the coronary system is difficult to construct accurately, and the Takagi-Sugeno (T-S) fuzzy model can approximate complex nonlinear systems with arbitrary precision. This paper studies the synchronization of the coronary systems based on the T-S fuzzy model. This paper considers the effect of time-delay on the system, combines Wirtinger integral inequality and a new double integral inequality to deal with the single integral and double integral after derivation, and reduces the conservatism of the system. Based on parallel distributed compensation scheme, the state feedback controller is designed, which effectively realizes the synchronization of the systems. Finally, the effectiveness of the method in this paper is realized through a simulation example.
Keywords:Coronary Artery System, Time-Varying Delay, T-S Fuzzy Model, Integral Inequality, Chaotic Synchronization

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
由于在信息学、医学、经济学、物理学、金融学等领域的广泛应用,混沌系统的同步在过去的几十年中引起了许多研究人员的关注 [1] [2] 。尤其是1990年代,混沌理论在生物医学领域的应用极大地推动了生物医学领域的发展。冠状动脉系统作为一种特殊的混沌系统,随着动脉直径和血管压力的不断变化,会产生复杂的非线性混沌动力学行为。血管的混沌行为会引起血管痉挛等心脑血管疾病。治疗心脑血管疾病,需要使血管的运动状态与正常血管的变化相同,这可以通过混沌控制来实现。因此,研究冠状动脉系统的同步问题是有意义的。
众所周知,研究者们已经提出了许多同步控制方案,包括滑模控制 [3] 、自适应控制 [4] 、模糊控制 [5] 、H∞控制 [6] 等。 [3] 研究了基于滑模控制的非线性时滞半马尔可夫跳跃系统的稳定性,作者构造了滑模控制律以保证系统的稳定性并使控制器系统在有限时间内达到预定的滑模面。Wang等人 [4] 提出了一种自适应控制方案,讨论了Chen系统在不同参数下的自适应同步问题,并分析了实现同步的理论条件。作者 [5] 设计了一种基于Lyapunov-Krasovskii (L-K)定理的新型模糊控制器,提高了闭环系统的最大延迟容限,实现了非线性神经网络系统的渐近稳定性。Long等人 [6] 通过动态反馈控制器研究了一类具有时变延迟的奇异系统的H∞控制问题。T-S模糊模型因其结构简单,便于描述的特点被广泛用于描述非线性系统,它的基本理论是将复杂非线性的系统通过模糊划分为多个简单的线性系统,并对每个模型的输出进一步进行模糊推理及判定,就可以得到复杂非线性系统。T-S模糊模型使得非线性系统可以利用线性系统的方法进行处理,进一步推动了对非线性系统的深入研究,简化了非线性系统的控制器设计及稳定性问题。
系统稳定性是控制领域的重要研究内容,是使系统正常运行的基础条件,因此尽可能少地寻求保守的稳定性条件是至关重要的。通常的方法是构造一个合适的L-K泛函以及对L-K泛函积分项的处理方法,构造L-K泛函没有统一的标准,积分项由原来的一重积分、二重积分,已经发展到现在的三重积分和四重积分,L-K泛函积分项的处理方法包括Jensen不等式 [7] 、Bessel-Legendre不等式 [8] 、自由权矩阵 [9] 和Wirtinger积分不等式 [10] 等。
在冠状动脉系统中,因不同患者对药物的吸收时间不同,时滞问题始终存在。值得注意的是,时滞的存在会降低系统性能,导致系统不稳定,因此需要充分考虑时滞的影响。此外,在治疗过程中存在一些难以预测的附加因素,如药物反应时间和情绪波动等,这些外部干扰使得系统并不能很好的达到理想的性能状态。冠状动脉系统的稳定性分析和同步控制方面已经取得了较多的理论成果,推动了该系统的发展和进步,虽然有其改善的一面,但是在条件的限制下不可避免地会存在系统保守性。考虑到冠状动脉血管在人体内的重要性,必须研究新的技术以改善现有的研究结果。
基于上述分析,本文主要研究了基于T-S模糊模型的冠状动脉时滞系统的同步问题。首先,用T-S模糊模型去逼近冠状动脉系统,得到该系统的数学模型;然后,构造合适的L-K泛函,结合Wirtinger积分不等式和一种新的二重积分不等式处理求导后的积分项,得到系统稳定的新判据;其次,设计状态反馈控制器,实现健康的冠状动脉系统及患病系统的同步,达到治疗疾病的目的;最后,通过实例验证上述方法的有效性。
2. 冠状动脉模型描述
2.1. 冠状动脉的数学模型
冠状动脉系统的数学模型可描述如下 [11] :
(1)
其中
, 分别表示血管内径差和静脉压,
表示血管在正常工作状态下的周期性扰动,
,,,, 是冠状动脉系统参数。给定参数初始值为
,,,, 和
,参数
随冠状动脉血管病变的变化而变化。当
时,系统(1)会出现混沌行为,图1表示系统(1)在没有控制输入和干扰时的混沌响应。

Figure 1. The trajectory of chaotic coronary artery system without any control input
图1. 无控制输入的混沌冠状动脉系统轨迹图
2.2. 基于T-S模糊模型的系统模型描述
对于冠状动脉时滞系统,用T-S模糊模型来描述具有r规则的主系统为:
规则i:If (
is
),(
is
) and ∙∙∙ and (
is
)
Then
(2)
其中
, 是模糊集,r是模糊规则的数量,
是前件变量,
是状态向量,其初始值为
, 表示主系统中的非线性函数,
表示周期性干扰,A和C是给定的常数矩阵。
通过采用乘积推理机,单点模糊化和加权平均解模糊化的模糊推理方法,对系统(2)进行模糊化处理可得:
(3)
其中
(4)
与上述过程类似,描述具有r规则的从系统为
规则i:If (
is
),(
is
) and ∙∙∙ and (
is
)
Then
(5)
其中
表示从系统中的非线性函数,
表示控制输入,
表示不确定的外部干扰,从系统的模糊模型可表示为:
(6)
定义误差系统
,则误差系统可以表示为:
(7)
其中
,非线性函数满足下列Lipschitz条件:
(8)
其中L是常数矩阵。
为实现主从系统的同步,设计具有模糊规则的状态反馈控制器:
控制器规则i:If (
is
),(
is
) and ∙∙∙ and (
is
) Then
(9)
其中
是增益矩阵,
是时滞函数且
,,与上述处理过程类似,得到模糊控制器为:
(10)
进一步处理误差系统
为
(11)
3. 相关引理
下面是本文需要用到的引理
引理1 [12] 对于任意对称矩阵
,标量
且满足
,和可微函数
,满足下列不等式:
(12)
其中,
,
引理2 [13] 对于任意正定矩阵
,和任意可微函数
,使下式成立:
(13)
其中
引理3 [14] 对于给定的矩阵
, 及标量
,假设存在对称矩阵Q,下列不等式成立:
(14)
4. 主要结果
系统稳定性分析
定理1:如果存在对称正定矩阵P,
,,合适维度的矩阵
, 和标量
,, 使下列不等式成立,则误差系统(11)趋于0,即误差系统是渐进稳定的。
(15)
其中
证明:构造合适的L-K泛函:
(16)
其中
将式(16)求导得
(17)
通过引理1和引理3可得,
其中
(18)
通过引理2可得,
同理可得
由(8)可得
(19)
其中
。
结合上述分析可得
(20)
其中
为了研究外部扰动,结合上述讨论定义下列式子
(21)
其中
,应用Schur补定理可得定理1,即定理1证明完毕。
5. 同步控制
定理2:如果存在给定的标量
,,,对称正定矩阵
,, 和合适维度的矩阵
,,使得下列不等式成立
(22)
其中
证明:证明过程与定理1的证明过程类似,在不等式(15)的两边分别乘对角阵
,并应用Schur补定理可以得到(22),其中
(23)
定理2证明完毕。
可以看到上述不等式中有类似于
的非线性项存在,不能直接用常规的LMI工具箱求解。基于将非凸可行性问题转化为凸优化问题的思想,通过锥补线性化方法解决这类非线性问题,即将(22)转化为下面求最小化的问题
使得
(24)
6. 仿真实验
考虑冠状动脉系统中的时延以及外部扰动,选取相关参数如下:
设计隶属度函数为
令
,,根据定理2可以得到增益矩阵
,
,
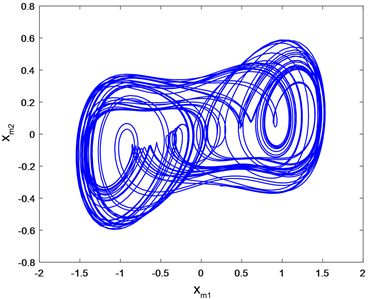
Figure 2. Coronary artery master-slave system trajectory diagram (without controller)
图2. 冠状动脉主从系统轨迹图(未加控制器)
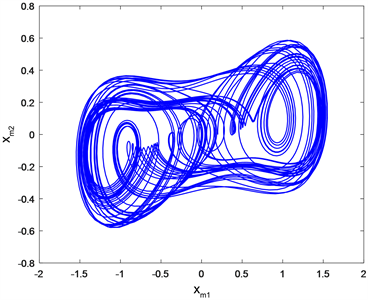
Figure 3. Coronary artery master-slave system trajectory diagram (with controller)
图3. 冠状动脉主从系统轨迹图(加控制器)
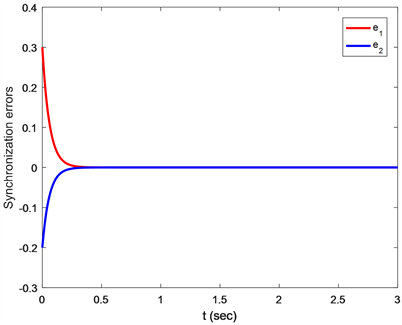
Figure 4. The trajectory of the error system under the controller
图4. 误差系统在控制器下的运动轨迹
图2表示未加控制器的主从系统相位图(左为主系统,右为从系统),图3表示加入控制器后的冠状动脉主从系统轨迹状态(左为主系统,右为从系统),图4表示控制器作用下的误差系统状态。从上数仿真图中可以看到,不处于控制状态时的主从系统是不同步的,其运动轨迹不相同,而在控制器的作用下二者的运动状态一样,实现了同步。并且在控制器的作用下,误差系统随着时间的变化逐渐趋于0,也验证了两个系统实现了同步,呈现出较为理想的治疗效果,验证了本文所提方法的有效性。
7. 结论
本文基于T-S模糊模型研究了冠状动脉时滞系统的同步问题。冠状动脉系统是一个复杂的非线性系统,利用T-S模糊模型去逼近该系统可以得到较为精确的数学模型,便于后续的研究分析。对于冠状动脉系统,本文对该系统进行了稳定性分析和同步控制研究,并且取得了理想的成果,对于治疗冠状动脉疾病及其并发症起到了良好的作用。
文章引用
曹秋霞. 基于T-S模糊模型的冠状动脉时滞系统同步研究
Synchronization Study for Coronary Artery Time-Delay Systems Based on T-S Fuzzy Model[J]. 计算机科学与应用, 2022, 12(02): 392-404. https://doi.org/10.12677/CSA.2022.122040
参考文献
- 1. 朱涛, 张广军, 姚宏, 李睿. 滑模控制的时滞分数阶金融系统混沌同步[J]. 深圳大学学报(理工版), 2014, 31(6): 626-629.
- 2. Tirandaz, H., Aminabadi, S.S. and Tavakoli, H. (2017) Chaos Synchronization and Parameter Identifica-tion of a Finance Chaotic System with Unknown Parameters, a Linear Feedback Controller. Alexandria Engineering Journal, 57, 1519-1524. https://doi.org/10.1016/j.aej.2017.03.041
- 3. Qi, W.H., Park, J.H., Cheng, J. and Kao, Y.G. (2017) Robust Stabilisation for Non-Linear Time-Delay Semi-Markovian Jump Systems via Sliding Mode Control. IET Control Theory & Applications, 11, 1504-1513.
https://doi.org/10.1049/iet-cta.2016.1465
- 4. Wang, Y.W., Guan, Z.-H. and Wen, X.J. (2004) Adaptive Synchro-nization for Chen Chaotic System with Fully Unknown Parameters. Chaos Solitons & Fractals, 19, 899-903. https://doi.org/10.1016/S0960-0779(03)00256-X
- 5. Marouf, S., Esfanjani, R.M., Akbari, A., et al. (2016) T-S Fuzzy Controller Design for Stabilization of Nonlinear Networked Control Systems. Engineering Applications of Artifi-cial Intelligence, 50, 135-141.
https://doi.org/10.1016/j.engappai.2016.01.031
- 6. Long, S.H. and Zhong, S.M. (2017) H∞ Control for a Class of Singular Systems with State Time-Varying Delay. ISA Transactions, 66, 10-21. https://doi.org/10.1016/j.isatra.2016.10.004
- 7. Wang, J.A., Wen, X.-Y. and Hou, B.-Y. (2020) Advanced Stabil-ity Criteria for Static Neural Networks with Interval Time-Varying Delays via the Improved Jensen Inequality. Neuro-computing, 377, 49-56.
https://doi.org/10.1016/j.neucom.2019.10.034
- 8. Seuret, A. and Gouaisbaut, F. (2015) Hierarchy of LMI Condi-tions for the Stability Analysis of Time-Delay Systems. Systems & Control Letters, 81, 1-7. https://doi.org/10.1016/j.sysconle.2015.03.007
- 9. Tan, J.Y., Dian, S.Y., Zhao, T. and Chen, L. (2017) Stability and Stabilization of T-S Fuzzy Systems with Time Delay via Wirtinger-Based Double Integral Inequality. Neurocompu-ting, 275, 1063-1071.
https://doi.org/10.1016/j.neucom.2017.09.051
- 10. Park, M.J., Lee, S.H., Kwon, O.M. and Ryu, J.H. (2018) En-hanced Stability Criteria of Neural Networks with Time-Varying Delays via a Generalized Free-Weighting Matrix Inte-gral Inequality. Journal of the Franklin Institute, 355, 6531-6548. https://doi.org/10.1016/j.jfranklin.2018.06.023
- 11. Lin, C.-J., Yang, S.-K. and Yau, H.T. (2012) Chaos Suppres-sion Control of a Coronary Artery System with Uncertainties by Using Variable Structure Control. Computers & Math-ematics with Applications, 64, 988-995.
https://doi.org/10.1016/j.camwa.2012.03.007
- 12. Seuret, A. and Gouaisbaut, F. (2013) Wirtinger-Based Integral Inequality: Application to Time-Delay Systems. Automatica, 49, 2860-2866. https://doi.org/10.1016/j.automatica.2013.05.030
- 13. Zhao, N., Lin, C., et al. (2017) A New Double Integral Ine-quality and Application to Stability Test for Time-Delay Systems. Applied Mathematics Letters, 65, 26-31. https://doi.org/10.1016/j.aml.2016.09.019
- 14. Liu, K. and Seuret, A. (2017) Comparison of Bounding Methods for Stability Analysis of Systems with Time-Varying Delays. Journal of the Franklin Institute, 354, 2979-2993. https://doi.org/10.1016/j.jfranklin.2017.02.007









