Statistics and Application
Vol.06 No.02(2017), Article ID:21219,7
pages
10.12677/SA.2017.62026
Throughput Analysis of Multi-Hop ARQ System Based on Two-Dimensional Markov Chain and Relay Aggregation
Boyi He, Suoping Li, Zufang Dou
School of Science, Lanzhou University of Technology, Lanzhou Gansu

Received: Jun. 11th, 2017; accepted: Jun. 26th, 2017; published: Jun. 30th, 2017

ABSTRACT
In this paper, we analyzed the throughput of multi-hop ARQ system based on the method of relay aggregation. Firstly, we defined the node-state of two-hop ARQ system which consisted of a pair of transceivers and one relay node, and obtained the four-state transition matrix by establishing a two-dimensional Markov chain, then obtained the state transition probability of relay nodes in two hop ARQ system. Secondly, in the N + 1-hop ARQ system composed of a pair of transceivers and N relay nodes, we used relay aggregation to merge N relay nodes into a super relay and made the N+1-hop system equivalent to the two-hop system in principle, then obtained the state transition probability of relay nodes in N + 1-hop ARQ system. Finally, we defined the state of the multi-hop ARQ system as “G” and “B”, and got eight-state of state transfer processes of multi-hop ARQ system by combining with the state of the super relay and direct channel, and obtained the analytical solution for the throughput of multi-hop ARQ systems based on the steady-state equation. In fact, it was shown that there was a unified method to study the throughput performance of multi-relay and multi-hop ARQ system.
Keywords:Relay Aggregation, ARQ, Markov Chain, Direct Channel, Throughput
基于二维Markov链和中继聚合方法的多跳ARQ系统吞吐量的分析
何博祎,黎锁平,窦祖芳
兰州理工大学理学院,甘肃 兰州
收稿日期:2017年6月11日;录用日期:2017年6月26日;发布日期:2017年6月30日

摘 要
本文主要基于中继聚合的研究方法对多跳ARQ系统的吞吐量进行了分析。首先,对由一对收发节点和一个中继节点组成的两跳ARQ系统的节点状态进行了定义,通过建立二维的Markov链得到了四阶的状态转移矩阵,并因而求得两跳ARQ系统中继节点的状态转移概率。其次,在讨论由一对收发节点和N个中继节点组成的N + 1跳ARQ系统时,我们采用中继聚合将N个中继节点合并成一个超级中继并使得N + 1跳系统在原理上等效于两跳系统,从而求得N + 1跳ARQ系统中继节点的状态转移概率。最后,把多跳ARQ系统自身的状态定义为“G”和“B”,结合超级中继和直传链路的状态我们得到了多跳ARQ系统状态转移过程的八个状态,并通过稳态方程求得了多跳ARQ系统吞吐量的解析式。事实上,我们的结果也证实了多中继和多跳ARQ系统的吞吐量研究有统一的方法,有利于后续研究的统筹规划。
关键词 :中继聚合,ARQ,Markov链,直传链路,吞吐量

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
无线传感器网络(Wireless Sensor Networks, WSNs)被公认为是继互联网之后的第二大网络,美国《技术评论》杂志于2003年评选出的将对人类社会具有深远影响的十大新兴技术中,WSNs位列第一。WSNs的应用十分广泛,在国土安全、军事、环境监测、智能交通、医疗卫生等领域已经成为不可或缺的一部分。但是,WSNs的发展和应用也面临着一些问题,而其最关键的问题之一就是抗衰落性差,这就对数据传输的可靠性提出了更高的要求,因而各种高能效可靠传输技术成为了无线通信研究的热点。作为一种有效的差错控制技术,协同自动重传请求(Cooperative Automatic Repeat reQuest, C-ARQ)协议 [1] [2] [3] 以其可靠的数据传输而被广泛地应用和研究。
对于无线信道的衰落,我们一般会建立有限状态的Markov链来刻画衰落信道,从而研究无线通信的数据传输情况和通信系统的性能。文献 [4] 提出了一种基于两状态的马尔科夫链的Gilbert Elliott信道模型,将信道定义为两种状态,即“好”(Good)状态和“坏”(Bad)状态,该模型也成为后续研究的一种基本方法。文献 [5] 提出了带有单中继的ARQ系统的三状态马尔科夫模型,分别以完全相关的瑞丽衰落信道和完全不相关的瑞丽衰落为背景讨论了ARQ系统的吞吐量性能,得出影响吞吐量的三个因素:信道是否相关、中继节点位置、链路的衰落余量。文献 [6] 分析了组播协同ARQ协议(MCARQ),通过建立三状态的马尔科夫链模型来描述数据的传输过程,并以对等的服务时间和理想的奈奎斯特脉冲为条件给出了一种有效的时延和能量分析模型。基于给出的分析模型,证实了MCARQ协议(Multicast CARQ)较MARQ (Multicast ARQ)有更优的时延和能效。文献 [7] [8] 将Gilbert Elliott信道模型和有限马尔科夫链模型进行了有效的结合并用来分析ARQ系统的性能,在文献 [7] 中Maymouna Ben Said等人提出了带有译码和发送(Decoding and Forwarding, DF)中继的多跳ARQ系统的三状态马尔科夫模型,并根据中继是否丢包对两跳ARQ系统的吞吐量性能进行了分析,遗憾的是文中对于大于两跳的多跳ARQ系统,并没有给出完整的吞吐量分析,也没有对ARQ系统的其它性能进行扩展分析;而文献 [8] 提出了一种节点协同的停等式ARQ方案(Node-Cooperative Stop and Wait, NCSW),开创性地用到了中继聚合的方法,即通过Gilbert Elliott信道理论将M个中继节点等效成一个超级中继节点,进而建立了八状态的马尔科夫链模型分析了系统的吞吐量和时延性能,然而这种研究方法并没有拓展到多跳ARQ系统性能上。
本文基于以上研究的成果,尤其是在文献 [8] 的中继聚合的基础之上,将中继聚合的方法应用到了多跳ARQ协议的吞吐量性能的求解上,使得多跳和多中继ARQ系统在吞吐量的研究上有了统一的方法。
2. 基于中继聚合的多跳ARQ协议
文献 [8] 中介绍了怎样使用中继聚合法求解多中继协同ARQ的吞吐量,接下来我们将此方法用来分析多跳ARQ的吞吐量性能,以期使多跳ARQ和多中继ARQ在吞吐量的求解方法上保持一致。多跳无线系统具有N个中继节点: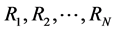 见图1,这N个中继节点将无线信道分成N + 2个传输信道,分别是:直传信道,即源节点S和目的节点D之间的信道;中间信道,即源节点S到第一个中继节点
见图1,这N个中继节点将无线信道分成N + 2个传输信道,分别是:直传信道,即源节点S和目的节点D之间的信道;中间信道,即源节点S到第一个中继节点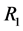 之间的信道;N个中继信道,即
之间的信道;N个中继信道,即 到
到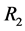 之间的信道、
之间的信道、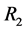 到
到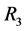 之间的信道、…、
之间的信道、…、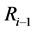 到
到 之间的信道、…、
之间的信道、…、 到目的节点D之间的信道。
到目的节点D之间的信道。
2.1. 两跳ARQ系统的节点状态模型
首先从两跳ARQ系统开始分析,两跳系统有一对收发节点和一个中继节点,将信道分成三个链路:直传链路、中间链路、中继链路,如图2所示。衰落信道的研究这里采用Gilbert Elliott信道模型,直传链路、中间链路和中继链路的两状态的概率转移矩阵分别为:
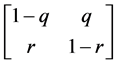 ,
,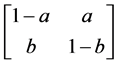 ,
,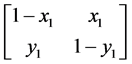
我们定义中继节点有G和B两个状态,用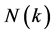 表示中继节点在
表示中继节点在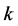 时隙的状态,其表达式及含义如下:
时隙的状态,其表达式及含义如下:
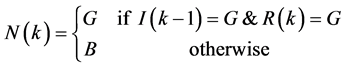 (1)
(1)
这里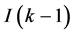 和
和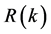 分别表示中间链路在
分别表示中间链路在 时隙、中继链路在
时隙、中继链路在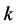 时隙的状态,只有当
时隙的状态,只有当 和
和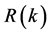 都是G状态时,中继节点的状态
都是G状态时,中继节点的状态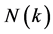 才是G状态,否则
才是G状态,否则 为B状态。
为B状态。 的四种情况用
的四种情况用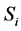 表示(
表示( ),其四状态的Markov链如图3。相应的概率转移矩阵为:
),其四状态的Markov链如图3。相应的概率转移矩阵为:
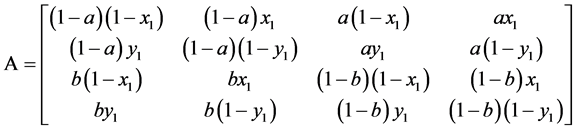 (2)
(2)
设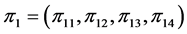 ,
,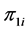 代表处于
代表处于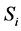 状态的概率,
状态的概率,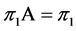 ,
,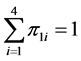 。
。 是一个两状态的Markov链,我们用转移参数
是一个两状态的Markov链,我们用转移参数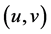 对其进行描述,其中
对其进行描述,其中 和
和 定义如下:
定义如下:
 ;
;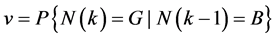 . (3)
. (3)
由图3中的Markov链可知: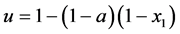 ,并根据条件概率的知识以及转移概率
,并根据条件概率的知识以及转移概率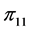 得:
得:

Figure 1. Multi-hop ARQ system
图1. 多跳ARQ系统

Figure 2. Two-hop ARQ model
图2. 两跳ARQ模型

Figure 3. State transition of two dimensional vector 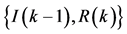
图3. 二维向量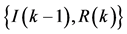 的状态转移
的状态转移
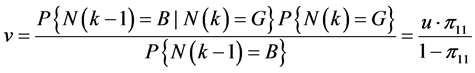 .
.
2.2. 多跳ARQ系统的节点状态模型
当中继节点数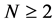 时,这里采用中继聚合法对中继节点逐步进行合并。首先,将中继节点
时,这里采用中继聚合法对中继节点逐步进行合并。首先,将中继节点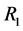 和中继节点
和中继节点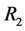 聚合成一个组合中继
聚合成一个组合中继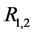 ,接着再用组合中继
,接着再用组合中继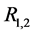 和中继节点
和中继节点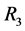 聚合形成新的更大的组合中继
聚合形成新的更大的组合中继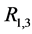 。如此,直到N个中继节点聚合成一个超级组合中继
。如此,直到N个中继节点聚合成一个超级组合中继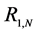 ,那情况就回到了两跳ARQ系统的情况。
,那情况就回到了两跳ARQ系统的情况。
用 和
和 分别代表中继
分别代表中继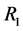 和中继
和中继 在
在 时隙的状态,
时隙的状态,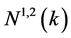 表示由中继
表示由中继 和
和 聚合成的组合中继
聚合成的组合中继 的状态,有:
的状态,有:
 (4)
(4)
同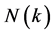 一样,
一样, 也是一个两状态的马尔科夫过程,用转移参数
也是一个两状态的马尔科夫过程,用转移参数 对其进行描述,其中
对其进行描述,其中 和
和 定义如下:
定义如下:
 ;
;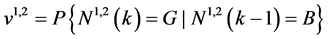 (5)
(5)
这里用 代表
代表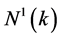 的Markov参数,而用
的Markov参数,而用 代表
代表 的Markov参数。其中
的Markov参数。其中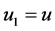 ,
,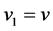 ;参数
;参数 亦是
亦是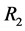 到
到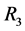 之间信道的Gilbert Elliott参数。显然
之间信道的Gilbert Elliott参数。显然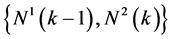 的情况有四种,用
的情况有四种,用 表示(
表示( ),其四状态的Markov链如图4所示。
),其四状态的Markov链如图4所示。
根据图4和(5)式有: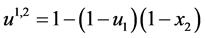 ,由
,由 和条件概率的知识求得
和条件概率的知识求得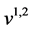 :
:

将组合中继 和中继
和中继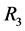 聚合为新的组合中继
聚合为新的组合中继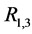 ,并用
,并用 表示其在
表示其在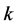 时隙的状态。用同样的方法,直到所有的中继节点聚合成一个超级组合中继,此时用
时隙的状态。用同样的方法,直到所有的中继节点聚合成一个超级组合中继,此时用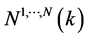 表示超级组合中继在
表示超级组合中继在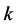 时隙的状态,转移概率参数如下:
时隙的状态,转移概率参数如下:
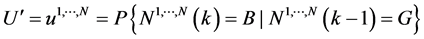 ;
;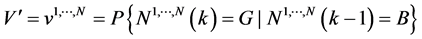 (6)
(6)

Figure 4. State transition of two dimensional vector 
图4. 二维向量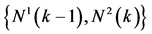 的状态转移
的状态转移
Table 1. State transition of
表1. 的状态转移
的状态转移
3. 多跳ARQ系统的吞吐量模型
本节根据上述思路,建立了针对于只有一个源节点、一个目的节点和一个“聚合”的组合中继的两跳ARQ方案,我们设定该ARQ协议只有两个状态:“T”状态,即源节点传输新的数据帧;“R”状态,即源节点和所有的协同节点重传数据帧。令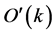 为ARQ系统在
为ARQ系统在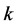 时隙的状态,这样该ARQ系统就是一个两状态的马尔科夫模型。其参数定义如下:
时隙的状态,这样该ARQ系统就是一个两状态的马尔科夫模型。其参数定义如下:
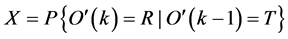 ;
;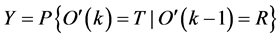 (7)
(7)
令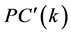 代表直传链路在
代表直传链路在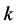 时隙的状态,综合考虑ARQ系统的状态
时隙的状态,综合考虑ARQ系统的状态 以及组合中继的状态
以及组合中继的状态 ,可以把ARQ系统的状态转移过程分为八个状态并建立八状态的Markov链。如表1给出了
,可以把ARQ系统的状态转移过程分为八个状态并建立八状态的Markov链。如表1给出了 的状态转移过程,其中八个状态分别为:
的状态转移过程,其中八个状态分别为: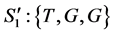 ,
, ,
,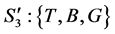 ,
,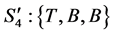 ,
,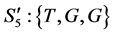 ,
, ,
, ,
,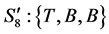 。与该模型相对应的转移概率矩阵如下:
。与该模型相对应的转移概率矩阵如下:
 (8)
(8)
并令 为平稳状态的概率向量,
为平稳状态的概率向量,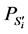 为平稳状态下系统处于状态
为平稳状态下系统处于状态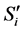 的概率。求解线性方程组,
的概率。求解线性方程组,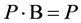 ,
,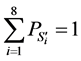 ,得到
,得到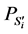 。从而得:
。从而得: ,
,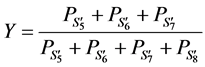 。
。
由此可得多跳ARQ协议的吞吐量的表达式:
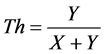 (9)
(9)
基金项目
本研究受教育部“春晖计划”合作科研项目(Z2016001)资助。
文章引用
何博祎,黎锁平,窦祖芳. 基于二维Markov链和中继聚合方法的多跳ARQ系统吞吐量的分析
Throughput Analysis of Multi-Hop ARQ System Based on Two-Dimensional Markov Chain and Relay Aggregation[J]. 统计学与应用, 2017, 06(02): 231-237. http://dx.doi.org/10.12677/SA.2017.62026
参考文献 (References)
- 1. Zhao, B. and Valenti, M. (2005) Practical Relay Networks: Ageneralization of Hybrid-ARQ. IEEE Journal on Selected Areas in Communications, 23, 7-18. https://doi.org/10.1109/JSAC.2004.837352
- 2. Choi, J. (2016) On HARQ-IR for Downlink NOMA Systems. IEEE Transactions on Communications, 64, 3576-3584. https://doi.org/10.1109/TCOMM.2016.2585651
- 3. Zorzi, M. and Rao, R.R. (2003) Geographic Random Forwarding (GeRaF) for Ad Hoc and Sensor Networks: Multi- Hop Performance. IEEE Transactions on Mobile Computing, 2, 337-348. https://doi.org/10.1109/TMC.2003.1255648
- 4. Zorzi, M., Rao, R. and Milstein, L. (1997) ARQ Error Control for Fading Mobile Radio Channels. IEEE Transactions on Vehicular Technology, 46, 445-455. https://doi.org/10.1109/25.580783
- 5. Marchenko, N. and Bettstetter, C. (2010) Incremental Cooperative Relaying in Time-Correlated Rayleigh Fading Channels. IEEE Global Telecommunications Conference, Miami, 6-10 December 2010, 1-5. https://doi.org/10.1109/glocom.2010.5683619
- 6. Li, S., Zhou, Y. and Zhou, Y. (2014) Delay and Energy Efficiency Analysis of Multicast Cooperative ARQ over Wireless Networks. Acta Informatica, 51, 51-60. https://doi.org/10.1007/s00236-013-0192-4
- 7. Ben Said, M. and Boujemaa, H. (2014) Three-State Markov Model for Mul-ti-Hop ARQ with DF Relaying. International Wireless Communications and Mobile Computing Conference, 4-8 August 2014, Nicosia, 930-935. https://doi.org/10.1109/iwcmc.2014.6906480
- 8. Dianati, M., Ling, X., Naik, K. and Shen, X. (2006) A Node-Cooperative ARQ Scheme for Wireless Ad Hoc Networks. IEEE Transactions on Vehicular Technology, 55, 1032-1044. https://doi.org/10.1109/TVT.2005.863426
