Statistics and Application
Vol.
11
No.
02
(
2022
), Article ID:
50274
,
13
pages
10.12677/SA.2022.112034
王氏保费准则下基于保险人与再保险人 双方视角下停止–损失再保险的 最优自留额研究
李匡亚1,李美平2
1江西财经大学金融学院,江西 南昌
2江西飞宏律师事务所,江西 吉安
收稿日期:2022年3月18日;录用日期:2022年4月6日;发布日期:2022年4月15日

摘要
这篇文章针对保险精算中停止–损失再保险模型,基于王氏保费准则的基础上,将原保险公司与再保险公司双方面临的风险结合起来考虑,以某种风险度量准则为一定的目标,通过数学工具最小化这一目标,讨论并得出相应的最优解。求解之后,假设保险人的初始面临的损失X服从指数分布,进行数值模拟,来比较最优自留额的值。
关键词
VaR (Value-at-Risk),王氏保费准则,停止–损失再保险,自留额,凸风险组合

Research on the Optimal Retention for a Loss-Stop Reinsurance from the Perspectives of Both Insurers and Reinsurers under Wang’s Premium Principle
Kuangya Li1, Meiping Li2
1School of Finance, Jiangxi University of Finance and Economics, Nanchang Jiangxi
2Jiangxi Feihong Law Office, Ji’an Jiangxi
Received: Mar. 18th, 2022; accepted: Apr. 6th, 2022; published: Apr. 15th, 2022

ABSTRACT
This article is aimed at the stop-loss model in reinsurance, based on Wang’s premium principle, combined with the perspectives of both the insurer and the reinsurer, taking the convex risk combination of total loss of both parties to the reinsurance contract as the objective function to solve, to find the existence of optimal retention and the expression of the solution. After the solution, it is assumed that if the initial loss X faced by the insurer obeys an exponential distribution, numerical simulations are performed to compare the value of the optimal retention.
Keywords:VaR (Value-at-Risk), Wang’s Premium Principle, Stop-Loss Reinsurance, Retention, Convex Risk Combination

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 研究背景与研究意义
再保险策略是保险公司分散其公司面临的风险的有效措施之一,主要指自身有着大量不确定风险的保险公司希望能缴纳一定的费用,使得自身所面临的风险能合理规避,遭受不必要的损失,使得再保险公司承担这部分风险。然而,原保险公司需要在其所支付的再保险保费以及其转移自身部分风险之间的大小之间进行权衡,使得原保险公司在购买再保险合同后,能最小化其面临的风险。同样地,对于再保险公司而言,也需要在其所收取的保费以及所接纳转移风险大小之间进行权衡。由此,保险精算中产生了一类研究在什么样的情况下,能使得这样缴纳的费用与其规避的风险之间存在精确而又“艺术性”的平衡的问题。在研究这类问题的过程中,学者们逐渐积累了一些常用的求解方式,例如,Borch [1] 使用保险精算中常见的期望值保费原理,以概率统计中方差的统计量度量原保险人面临的风险,最小化其值求解出最优的解。Vajda [2] 选取的角度和Borch不同,他基于承保转移风险的再保公司入手,但求解方法和Borch类似,使用概率统计中方差来度量再保险人面临的风险,求解最优解。Cai J. (2016) [3] 结合原保险公司与再保险公司双方的视角,以最小化双方的VaR风险测度凸组合为目标,求解出相应的最优再保险合同形式。此外,在求解最优的再保险形式中,保险精算中还采取最大化期望效用的准则。例如Arrow [4] 以期望值保费原理为基础,在最大化期望效用的原则上,求解出相应的最优再保险形式。Kaluszka和Okolewski [5] 分析在固定再保险费用下以最大可能发生索赔的期望效用为目标函数,求解相应的再保险形式。
求解出的最优保险形式一般是停止–损失再保险和比例再保险,停止–损失再保险具有特别重要的理论意义以及相关的应用价值。Cai J.等(2007)和Cai J.等(2008) [6] [7] 基于期望值保费原理,从原保险人的角度出发,计算出停止–损失再保险的最优自留额,同时对相应的模型进行了一定的推广。更进一步,杨博 [8] 从原保险人的角度出发,基于方差相关的保费原理,有序分类讨论了以风险价值(VaR)和条件尾部期望(CTE)度量风险的标准,通过一系列数学运算,得出最优自留额。
在现实的生活中,一份质量好的再保险合同应该考虑原保险人与再保险人双方的视角。Borch [9] 指出一份再保险合同需要基于投保再保险合同的保险人与承保再保险合同的再保险人双方的角度,基于相应的准则下得出相应最优标准下的再保险模式。鉴于以上文献,本文考虑原保险人与再保险人双方的视角下,来构造相应最优的停止–损失再保险。
本文基于Cai J.等(2007) [6] 和Cai J.等(2016) [3] 两篇文章,本文假定原保险人面临的初始的总损失X服从指数分布,用能包含期望值保费原理的王氏保费作为原保险人缴纳再保费计算的准则,同时综合考虑原保险人与再保险人两方的利益,构造风险凸组合为目标函数,最小化其值,对停止–损失再保险模型中最优自留额的存在性进行一定探讨,同时求出王氏保费原理下最优自留额的表达式。
1.2. 基本概念
假设非负随机变量
是给定时间内保险合同中保险人面临的总损失。
根据概率论的基础知识,可进一步假设X的累积分布函数
,其对应生存函数
,根据非负随机变量的性质,可知其均值大于零。接下来,构造随机变量
表示原保险人自留风险,
再保险人承保后自留风险,故停止–损失再保模型为:
参数
为停止–损失再保险的自留额,
,且
。
定义1
在置信水平
的条件下,
风险度量定义 [10] :
(1)
此外,根据
的定义可知,
, 是生存函数
的反函数。
定义2王氏保费准则
文献 [11] [12] 用调整后的保费来代替保费的期望值。
对于任一风险损失变量X,定义:
(2)
上式称作王氏保费原理(也称作扭曲函数保费原理),其中
是安全载荷系数,定义
是增的凹函数且满足:1)
;2)
。
根据停止–损失再保险模型的式子以及王氏保费的表达式,可假设
为原保险公司需要支付给再保险公司分出风险的保费,其现实的意义是
是关于d的递减函数,直观的解释是原保险人自留的风险越多,其所缴纳的再保险保费也就越少。
现假设保险人的自留损失以及其总损失分别为XI、XTI,再保险公司所承包的分出损失以及总损失为XR、XTR。根据相关的定义可以知道,原保险公司或再保险公司签订再保险合同后,其面临的总损失包含自留损失和再保险保费两个部分,用数学表达式表达为:
(3)
(4)
对于度量风险的VaR,我们定义:
(5)
(6)
2. 基于王氏保费准则下以VaR为风险度量的凸组合的最优自留额
2.1. 模型构建
考虑原保险人和再保险人两方的视角的凸风险组合,假设
为原保险人的置信水平,
为再保险人的置信水平。
首先,求出停止–损失再保险关于
的生存函数为:
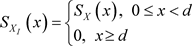 (7)
(7)
接下来,可根据生存函数VaR的关系来求出原保险人自留风险的VaR的表达式,当
时,那么
,当
时,
。综合两项的分析:
(8)
对于一个给定的常数
,可得:
(9)
然后再保险人自留风险的生存函数
:
(10)
同理,可求出再保险人的
。如果
时,那么
,如果
,那么
,则其表达式:
(11)
可得:
(12)
现定义以VaR为度量风险的凸组合的目标函数 [11] 为
(13)
在上述的目标函数表达式中,
为凸组合式子的权重。考虑特殊情形,
时,这款再保险合同完全只是站在再保险人的角度考虑其风险;而当
时,这款再保险合同完全只是站在原保险人的角度考虑其风险。
时,这款再保险产品能够同时将保险人与再保险人双方的视角考虑在内分析其风险,给现实生活中保险公司产品定价有一定借鉴意义。
根据VaR的性质以及文献 [13],可得到目标函数的表达式
(14)
我们目前主要是通过最小化目标函数:
(15)
表示最优自留额。
在最优自留额的求解过程中,权重
的大小体现了停止–损失再保险的最优自留额决策中原保险人和再保险人风险的重要水平。下面就
、
和
三种情况各自进行研究,现令
(16)
2.2. 模型求解
1) 偏向于考虑再保险人风险的最优自留额
在构造出的凸风险目标函数中,若要更多的偏向考虑再保险人所面临的风险,则权重
。
定理1
当
时,a) 最优自留额
有解的充分必要条件是
和
成立;
b) 如果a)中讨论的条件成立的话,自留额
有最优解,为
或相同的表达式
,并且此时VaR的凸风险组合的最小值为
。
证明:a)当再保险模型基于王氏保费原理时,则其保费:
,其中
是相对安全负荷系数。
现在的目标是要求
在
的整个区间内的最小风险,对d求导,可得:
令
,可得
,。由于
,故
,同时根据王氏保费中扭曲函数的性质,知
是递减函数,所以
。当
时,
,当
时,
,当
时,
,当
时,
,则
在
处为目标最小。考虑
导数与零之间的大小关系及其与极值的关系,故还需要考虑
时的情况,要使得
在
处取到最小值,即自留额有最优解的情况,还需要满足:
,化简即可得到
。值得注意的是,
,可得到
,即
。
b)如果a)中讨论的条件成立的话,自留额
有最优解,为
或相同的表达式
。
定理2
当
,a)最优自留额
有解的充分必要条件是
成立;
b)假如上面的不等式成立,停止–损失再保险的自留额
存在最优解,
或者以VaR表示的相同数学表达式
,并且此时目标函数VaR的凸风险组合的最小值为
。
证明:a) 当再保险模型基于王氏保费原理时,则其保费:
,其中
是相对安全负荷系数。
则对应目标函数
的表达式:
(17)
现在的目标是要求
的最小值,根据高等数学的相关知识,现就
对d求导,可得:
(18)
令
,可得
,,因为
,就
, 可舍去。同时
,所以
。下面就d的不同取值来进行分类讨论,当
时,
,当
时,
,当
时,
,当
时,
,则
在
处取到最小值。
另外值得注意的是,
,可得到
,即
。
b) 如果上述讨论的不等式成立的话,自留额
存在,为
或相同的表达式
。
此时目标函数VaR的凸风险组合的最小值为
。
定理3
当
时,a) 自留额
有最优解的充分必要条件是
,并且满足
;
b) 如果a)中讨论的条件成立的话,停止损失再保险自留额
有最优解,为
或相同的表达式
,并且此时VaR的凸风险组合的最小值为
。
证明:a) 当再保险模型基于王氏保费原理时,则其保费:
,其中
是相对安全负荷系数。
则对应目标函数
的表达式:
(19)
现在的目标是要求
的最小值,根据高等数学的相关知识,现就
对d求导,可得:
(20)
令
,可得
, 时,
,当
时,
,当
时,
,则
在
处取到最小值。根据上述讨论的情况,还需要考虑
时的情况,要使得
在
处取到最小值,即最优自留额存在,需要满足
,化简即可得到
。
值得注意的是,
,可得到
,即
。
b)如果a)中讨论的条件成立的话,停止损失再保险自留额
有最优解,为
或相同的表达式
,并且此时VaR的凸风险组合的最小值为
。
2) 偏向于考虑原保险人风险的最优自留额
当权重
时,即更多的偏向考虑原保险人所面临的风险。其求解的过程和
求解的过程类似。在详细的求解之后,可得到下面的定理。
定理4
当
时,a) 最优自留额
有解的充分必要条件为
,并且满足
;
b) 假如上面的不等式成立,停止–损失再保险的最优自留额存在,
或相同的表达式
,并且此时凸风险组合的最小值为:
。
证明:当再保险模型基于王氏保费原理时,则其保费:
,其中
是相对安全负荷系数。
对应目标函数
的表达式和定理1中证明的表达式一样,现在的目标是要求
的最小值,根据高等数学的相关知识,现就
对d求导,可得:
(21)
令
,可得
,,因为
,所以
,故
,进一步可得进一步可得当
时,
。当
时,
,当
时,
,当
时,
,当
时,
,则
在
处取到最小值。根据上述讨论的情况,还需要考虑
时的情况,要使得
在
处取到最小值,即最优自留额存在,还需要满足:
。
值得注意的是,
,可得到
,即
。
b) 假如上面的不等式成立,停止–损失再保险的最优自留额存在,
或相同的表达式
。
此时VaR的凸风险组合的最小值为
。
定理5
当
,a) 最优自留额
有解的充分必要条件
,并且满足
;
b) 假如上面的不等式成立,停止–损失再保险的最优自留额存在,
或者以VaR表示的相同数学表达式
,并且此时目标函数VaR的凸风险组合的最小值为
。
证明:a) 当再保险模型基于王氏保费原理时,则其保费:
,其中
是相对安全负荷系数。
则对应目标函数
的表达式和定理2证明过程中的表达式一样,现在的目标是要求
的最小值,根据高等数学的相关知识,现就
对d求导,可得:
(22)
令
,可得
,,因为
,就
,类似定理1的证明可得到不等式
。下面就d的不同区间取值来进行分类讨论,当
时,
,当
时,
,当
时,
,当
时,
,则
在
处取到最小值。根据上述的情况,还需要考虑
的情况,要使得
在
处取到最小值,即最优自留额存在,还需要满足
。值得注意的是,
,可得到
,即
。
b) 如果上述讨论的不等式成立的话,最优自留额
存在,为
或相同的表达式
。
定理6
当
时,a) 最优自留额
有解的充分必要条件是
,并且满足
;
b) 假如上面的不等式成立,停止–损失再保险的最优自留额存在,为
或相同的表达式
,并且此时VaR的凸风险组合的最小值为
。
证明:a) 当再保险模型基于王氏保费原理时,则其保费:
,其中
是相对安全负荷系数。
则对应目标函数
的表达式和定理2证明过程中的表达式一样。现在目标是要求
的最小值,根据高等数学的相关知识,现就
对d求导,可得:
(23)
令
,可得
, 时,
,当
时,
,当
时,
,则
在
处取到最小值。根据上述的情况,还需要考虑
的情况,要使得
在
处取到最小值,即最优自留额存在,还需要满足
。值得注意的是,
,可得到
,即
。
b) 如果上述讨论的不等式成立的话,最优自留额
存在,为
或相同的表达式
。此时VaR的凸风险组合的最小值为
。
3) 等权重系数情况下的最优自留额
在停止–损失再保险模型中,权重
表示等同的考虑再保险合同中原保险人与再保险人的风险,这时的最优自留额有着比较特殊的形式。即为如下所述的定理
定理7
当
时,a) 自留额
有最优解;
b) 最优自留额
或相同的表达式
,并且此时VaR的凸风险组合的最小值为
。
证明将权重
代入定理1中证明过程
的表达式中:
(24)
显然:
,此时VaR的凸风险组合的最小值为
。
定理8
当
时,a) 自留额
有最优解;
b) 最优自留额
或相同的表达式
,并且此时VaR的凸风险组合的最小值为
。
证明:将权重
代入定理2中证明过程
的表达式中:
(25)
显然:
此时VaR的凸风险组合的最小值为
。
定理9
当
时,a) 最优自留额
存在;
b) 假如上面的不等式成立,停止–损失再保险的最优自留额存在,
取正实数中某一任意值,并且此时VaR的凸风险组合的最小值为
。
证明:当
时,且再保险保费满足王氏保费原理时,
为常数
,即证。
3. 数值算例与分析
3.1. 参数构建
假设X服从指数分布,分布函数为
生存函数为
。
根据第二部分求解最优自留额的过程,可知影响停止–损失再保险合同中最优自留额的因素不仅仅是再保险双方的权重系数,还有保费收取的安全载荷系数以及原保险人和再保险人的置信水平,以及扭曲函数的形式。为了方便计算,本文选取扭曲函数
,以及
和
,并对定理1~6进行相应的数值计算。
3.2. 定理验证与分析
下面验证定理1,当
, 时,数据表如下。
根据表1可以了解到,在偏重考虑再保险人的利益角度时(
)且
时,自留额的最优解对双方置信水平的变化比较敏感,在其他条件不变的情况下,自留额最优解的大小与原保险人的风险容忍度
呈现负相关,与再保险人的风险容忍度
也为负相关关系。

Table 1. Variation in optimal retention due to changes in mutual confidence levels and their existence
表1. 双方置信水平变化引起的最优自留额的变化及存在情况
当
,, 时,下面验证定理2。

Table 2. Variation in optimal retention due to changes in the relative safety load factor and their existence
表2. 相对安全载荷系数变化引起的最优自留额的变化及存在情况
根据表2可以了解到,在偏重考虑再保险人的利益角度时(
)且
时,自留额的最优解对安全载荷系数
的变化较为敏锐,在其他条件不变的情况下,自留额最优解的大小与安全载荷系数
的变化呈现正相关关系。
当
, 时,定理3进行验证。

Table 3. Variation in optimal retention due to changes in the relative safety load factor and their existence
表3. 相对安全载荷系数变化引起的最优自留额的变化及存在情况
根据表3可以了解到,在偏重考虑再保险人的利益角度时(
)且
时,自留额的最优解与安全载荷系数
的变化无关系,但组合风险的数值与安全载荷系数的
的变化有关。
当
时,且
,,下面对定理4进行数值验证。

Table 4. Variation in optimal retention due to changes in the relative safety load factor and their existence
表4. 相对安全载荷系数变化引起的最优自留额的变化及存在情况
根据表4可以了解到,在偏重考虑原保险人的利益角度时(
),且
时,自留额的最优解对安全载荷系数
的变化较为敏锐,在其他条件不变的情况下,自留额最优解的大小与安全载荷系数
的变化呈现正相关关系。
当
时
,,下面对定理5进行数值验证。

Table 5. Variation in optimal retention due to changes in the relative safety load factor and their existence
表5. 相对安全载荷系数变化引起的最优自留额的变化及存在情况
根据表5可以了解到,在偏重考虑原保险人的利益角度时(
),且
时,自留额的最优解对安全载荷系数
的变化较为敏锐,在其他条件不变的情况下,自留额最优解的大小与安全载荷系数
的变化呈现正相关关系。
当
,且
时,下面对定理6进行数值验证。

Table 6. Variation in optimal retention due to changes in mutual confidence levels and their existence
表6. 双方置信水平变化引起自留额最优解变化及存在情况
根据表6可以了解到,在偏重考虑原保险人的利益角度时(
),且
时,自留额有最优解时对双方的风险容忍水平
要求较高,当
时,自留额最优解仍然没有,当
时,自留额最优解才相应有。
4. 结论
本文所讨论的凸风险组合模型具有更一般的意义,它既包括仅从原保险人的视角来求解最优形式的问题,也包括从再保险人的利益的角度来考虑最优形式的问题,因此无论是对于原保险人还是再保险人都具有特殊的现实意义。此外,在现实的生活中,具有免赔额的停止损失的保险产品在医疗、汽车等方面使用范围较广,本文能为这些保险公司提供一些保险产品定价的参考价值。
文章引用
李匡亚,李美平. 王氏保费准则下基于保险人与再保险人双方视角下停止–损失再保险的最优自留额研究
Research on the Optimal Retention for a Loss-Stop Reinsurance from the Perspectives of Both Insurers and Reinsurers under Wang’s Premium Principle[J]. 统计学与应用, 2022, 11(02): 323-335. https://doi.org/10.12677/SA.2022.112034
参考文献
- 1. Borch, K. (1960) An Attempt to Determine the Optimum Amount of Stop Loss Reinsurance. Transactions of the 16th International Congress of Actuaries, 1, 597-610.
- 2. Vajda, S. (1962) Minimum Variance Reinsurance. ASTIN Bulletin, 2, 257-260.
https://doi.org/10.1017/S0515036100009995
- 3. Cai, J., Lemieux, C. and Liu, F. (2016) Optimal Reinsurance from the Perspectives of Both an Insurer and a Reinsurer. ASTIN Bulletin, 46, 815-849.
https://doi.org/10.1017/asb.2015.23
- 4. Arrow, K.J. (1965) Uncertainty and the Welfare Economics of Medical Care. American Economic Review, 55, 154-158.
- 5. Kaluszka, M. and Okolewski, A. (2008) An Extension of Arrow’s Result on Optimal Reinsurance Contract. Journal of Risk and Insurance, 75, 275-288.
https://doi.org/10.1111/j.1539-6975.2008.00260.x
- 6. Cai, J. and Tan, K.S. (2007) Optimal Retention for a Stop-Loss Reinsurance under the VaR and CTE Risk Measures. ASTIN Bulletin, 37, 93-112.
https://doi.org/10.1017/S0515036100014756
- 7. Cai, J., Tan, K.S, Weng, C. and Zhang, Y. (2008) Optimal Reinsurance under VaR and CTE Risk Measures. Insurance: Mathematics and Economics, 43, 185-196.
https://doi.org/10.1016/j.insmatheco.2008.05.011
- 8. 杨博, 吴黎军. 方差相关保费原理下基于VaR和CTE下停止-损失再保险的最优自留额比较研究[J]. 统计学与应用, 2016, 5(2): 179-195.
- 9. Borch, K. (1969) The Optimal Reinsurance Treaty. ASTIN Bulletin, 5, 293-297.
https://doi.org/10.1017/S051503610000814X
- 10. Jorion, P. (2000) Value at Risk: The New Benchmark for Managing Phase-Type Distributions. Journal of Applied Probability, 42, 810-825.
- 11. 杜军红, 李智明, 吴黎军. 王氏保费准则下隐含再保险公司违约风险的最优再保险设计[J]. 应用概率统计, 2019, 35(1): 73-85
- 12. Wang, S. (1996) Premium Calculation by Transforming the Layer Premium Default Risk. ASTIN Bull, 26, 71-92
- 13. 谭显中, 温利民. 混合再保险中凸风险组合的最优再保险测量[J]. 应用概率统计, 2021, 37(4): 361-376.






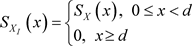 (7)
(7)