寨卡病毒溶瘤治疗脑癌的数学模型动力学分析 Dynamic Analysis of Mathematical Model in Brain Cancer Treatment by Zika Virus Oncolysis

doi:10.12677/AAM.2019.82032

Advances in Applied Mathematics
Vol. 08 No. 02 ( 2019 ), Article ID: 28970 , 15 pages
10.12677/AAM.2019.82032

Dynamic Analysis of Mathematical Model in Brain Cancer Treatment by Zika Virus Oncolysis

Tingmei Yang, Jian Liu

●How to Cite this Article

School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong

Received: Jan. 30^th, 2019; accepted: Feb. 14^th, 2019; published: Feb. 22^nd, 2019

ABSTRACT

Based on the Zika Virus specifically targeting to kill glioma stem cells, and having no effect on normal cells, we build a mathematical model about normal cells and brain tumor cells competing nutrient in culture dish adding Zika Virus Oncolytic therapy by analyzing the existence and stability of the equilibrium, and get the minimum effective dose parameters expression when the Oncolytic virus therapy is the most effective. Finally, we can verify the result by numerical simulation.

Keywords:Zika Virus, Brain Cancer, Oncolytic Therapy, Stability, Drug Dose, Numerical Simulation

寨卡病毒溶瘤治疗脑癌的数学模型动力学分析

杨婷梅，刘建

广州大学数学与信息科学学院，广东广州

收稿日期：2019年1月30日；录用日期：2019年2月14日；发布日期：2019年2月22日

摘要

本文基于寨卡病毒特异性靶向杀害脑瘤细胞中的胶质瘤干细胞，而对正常细胞没有影响的原理，建立一个在正常细胞和脑肿瘤细胞竞争营养液的培养皿中，添加寨卡病毒溶瘤治疗的数学模型。分析系统中平衡点的存在性与稳定性，当脑肿瘤细胞灭绝时，溶瘤病毒治疗效果最佳，并给出最小的有效药物剂量参数表达式。最后，通过数值模拟来验证我们所得到的结论。

关键词 :寨卡病毒，脑癌，溶瘤治疗，稳定性，药物剂量，数值模拟

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

溶瘤病毒治疗是一种新兴的而且有前景的癌症治疗方法，关于溶瘤病毒特异性攻击杀害肿瘤细胞，而对非癌性细胞没有影响的研究，前人已经做了大量的工作，建立了许多数学模型，也在医学领域得到了广泛的应用 [1] - [6] 。本文主要研究寨卡病毒溶瘤治疗脑恶性胶质瘤。

恶性胶质瘤亦称脑癌，是一种恶性程度最高的原发性颅内脑肿瘤。由于肿瘤生长快、侵袭性强，常规手术、放疗、化疗等治疗后复发率极高，预后差，绝大多数患者生存低于2年 [7] 。恶性胶质瘤的成因复杂，最新的研究显示，胶质瘤干细胞在其中发挥了关键作用，胶质瘤干细胞是一群能无限增殖，自我更新和多向分化的干细胞，不仅参与肿瘤血管生成，而且能够抵抗放化疗的杀瘤作用。所以，胶质瘤干细胞作为靶标的新型疗法成为当前的研究热点之一 [8] 。最近美国科学家团队进行合作研究发现，寨卡病毒可特异性感染并杀伤脑癌细胞中的干细胞，而不会感染非癌性脑神经细胞，于是寨卡病毒有望发展为新型溶瘤病毒，与常规手段结合或可提高此类癌症患者的生存几率 [9] 。于是他们向脑癌患者切除肿瘤样本和健康人神经培养物中分别引入寨卡病毒。7天后，发现寨卡病毒在特定脑瘤细胞中复制，并阻止这些细胞增殖，而人神经组织培养物的生长基本未受影响。基于上述结果，研究人员尝试利用小鼠体内分离的寨卡病毒治疗患脑瘤的小鼠，2周后发现，接受溶瘤病毒治疗的小鼠比接受安慰剂的小鼠肿瘤要小得多，存活时间更长。寨卡病毒溶瘤治疗机制在于宿主体内胶质瘤干细胞中缺乏有效的干扰素信号反应，而分化型胶质瘤细胞、神经元细胞和胶质细胞中由于存在较强的干扰素反应，寨卡病毒无法有效感染和复制。于是利用I型干扰素抗体处理分化型胶质瘤细胞后，寨卡病毒的感染率和杀伤效应得到显著提高 [10] 。

寨卡病毒是由伊蚊属蚊虫叮咬传播的黄病毒，与登革热和基孔肯雅病毒类似，其临床症状有发热，斑丘疹，关节痛，非化脓性的结膜炎等，自1947年首次在乌干达被发现以来，已经在非洲、东南亚和美洲等地造成多次爆发流行。迄今，全世界已有30多个国家报道寨卡病毒感染并引发多个国家输入性病例，其中大部分为美洲国家。2016年2月我国确诊了中国大陆首例境外输入性寨卡病毒感染病例，随后在广东、北京、浙江等地相继发现输入性病例。其感染风险和传播速度和对社会的危害已经受到包括公共卫生部门，疾病控制部门的高度关注 [11] 。该病毒最大的危害在于对孕妇腹中的胎儿发育具有较大影响，可造成新生儿脑部发育不全，患上“小头畸形症”。因为在新生婴儿的大脑中，存在大量种类不同的干细胞，这就是为什么寨卡病毒会给婴儿脑部带来如此严重损伤的原因。反之，在成人大脑中很少干细胞，这意味着寨卡病毒将只摧毁那些形成肿瘤的干细胞，而不会破坏健康脑细胞。

2. 基础模型

2017年，王子子建立了一个基于细胞增长的抑制的溶瘤病毒治疗模型 [12] 。该文章在正常细胞和肿瘤细胞竞争的反应扩散模型基础上，结合算子半群理论推导，引入溶瘤病毒项，并得到肿瘤细胞根除平衡点的全局稳定性条件。具体模型如下：

${\begin{cases} \partial_{t} u_{1} (t, x) = d_{1} Δ u_{1} (t, x) + u_{1} (t, x) (a_{1} - b_{1} u_{1} (t, x) - c_{1} u_{2} (t, x)), t > 0, x \in Ω, \\ \partial_{t} u_{2} (t, x) = d_{2} Δ u_{2} (t, x) + u_{2} (t, x) (a_{2} - b_{2} u_{1} (t, x) - c_{2} u_{2} (t, x)) \\ - μ u_{2} (t, x) u_{3} (t, x), t > 0, x \in Ω, \\ \partial_{t} u_{3} (t, x) = d_{3} Δ u_{3} (t, x) + B - d u_{3} (t, x) + γ μ \int_{Ω} Γ (x, y, τ) u_{2} (t - τ, y) u_{3} (t - τ, y) d y, t > 0, x \in Ω, \\ \partial_{n} u_{1} = \partial_{n} u_{2} = \partial_{n} u_{3} = 0, t > 0, x \in Ω, \\ u_{1} (θ, x) = u_{1}^{0} (θ, x), u_{2} (θ, x) = u_{2}^{0} (θ, x), u_{3} (θ, x) = u_{3}^{0} (θ, x), θ \in [- τ, 0], x \in Ω . \end{cases}$

其中 $u_{1}, u_{2}, u_{3}$ 表示正常细胞，肿瘤细胞和病毒， $a_{1}, a_{2}$ 是正常细胞，肿瘤细胞的内禀增长率， $b_{1}, c_{2}$ 是密度制约因素， $c_{1}, b_{2}$ 是竞争系数，d是病毒的死亡率， $d_{i}$ 是扩散系数 $i = 1, 2, 3$ ， $Δ$ 是Laplacian算子，系统第二个方程中的 $μ u_{2} (t, x) u_{3} (t, x)$ 反应了病毒毒素对肿瘤细胞的杀害能力。 $Ω$ 是空间内 $R^{n}$ 的孤立有界且具有光滑边界 $\partial Ω$ 的有界集，且满足边界条件 $\partial_{n} u_{1} (t, x) = \partial_{n} u_{2} (t, x) = \partial_{n} u_{3} (t, x), t > 0, x \in \partial Ω$ ，这意味着任意元素 $u_{i}$ 到达边界 $\partial Ω$ 时，其不会走出区域。

针对以上背景材料，我们提出一个简单的常微分模型，考虑在体外培养正常细胞，脑肿瘤细胞，并添加寨卡病毒药物补充量，探究它们的动力学行为。我们不妨提出以下假设条件：1) 正常细胞和肿瘤细胞在培养器里是竞争关系，单纯考虑对营养液的竞争，不考虑空间等其他资源的竞争；2) 体外模型，一般不考虑特异性免疫反应；3) 溶瘤治疗效果主要通过讨论最优的参数塞卡病毒补充药物剂量B使得脑肿瘤细胞灭绝。我们建立如下模型：

${\begin{cases} \frac{d x}{d t} = x (a_{1} - b_{1} x - c_{1} y), \\ \frac{d y}{d t} = y (a_{2} - b_{2} y - c_{2} x) - r_{1} y z, \\ \frac{d z}{d t} = B + r_{2} y z - d z . \end{cases}$ (1)

其中 $x, y, z$ 分别表示正常细胞，脑肿瘤细胞，寨卡病毒的数量， $a_{1}, a_{2}$ 表示正常细胞，肿瘤细胞的内禀增长率， $b_{1}, b_{2}$ 分别表示密度制约因素， $c_{1}, c_{2}$ 分别表示竞争系数， $r_{1}$ 是寨卡病毒的侵染率， $r_{2}$ 是寨卡病毒的释放率，d是寨卡病毒的死亡率，B是药物补充量。以上参数均为正的。

3. 系统的非负性和有界性分析

引理3.1：设 $(x, y, z)$ 是在满足初始条件 $x (0) > 0, y (0) > 0, z (0) > 0$ 下模型(1)的解，则所有解都是非负的，并且最终有界。

证明：(反证)假设存在最小的时间 $t_{1} > 0$ 使得 $z (t_{1}) = 0$ ，把 $z (t_{1})$ 代入模型(1)的第三个方程有 $\frac{d z}{d t} = B > 0$ ，则对 $\forall ε > 0$ ，当 $t \in (t_{1} - ε, t_{1})$ 有 $z (t) < 0$ ，由于 $t_{1}$ 是 $z (t_{1}) = 0$ 的最小时间且 $z (0) > 0$ ，由解对初值的连续依赖性，则必有 $z (t) > 0$ 与前面假设矛盾。故对 $\forall ε > 0$ 有 $z (t) > 0$ 同理可证，对 $\forall ε > 0$ 有 $x (t) \geq 0, y (t) \geq 0$ 。

下证系统(1)的有界性，先考虑竞争系统

${\begin{cases} \frac{d x}{d t} = x (a_{1} - b_{1} x - c_{1} y), \\ \frac{d y}{d t} = y (a_{2} - b_{2} y - c_{2} x) . \end{cases}$ (2)

得到平衡点

$(0, 0), (\frac{a_{1}}{b_{1}}, 0), (0, \frac{a_{2}}{b_{2}}), (\frac{a_{2} c_{1} - a_{1} b_{2}}{c_{1} c_{2} - b_{1} b_{2}}, \frac{a_{1} c_{2} - a_{2} b_{1}}{c_{1} c_{2} - b_{1} b_{2}}) .$

构造直线

$l \equiv y + x - M,$

$M = \max {\frac{a_{1}}{b_{1}}, \frac{a_{2}}{b_{2}}, \frac{a_{2} c_{1} - a_{1} b_{2} + a_{1} c_{2} - a_{2} b_{1}}{c_{1} c_{2} - b_{1} b_{2}}} .$

由于

$\begin{array}{l} \frac{d l}{d t} = \frac{d y}{d t} + \frac{d x}{d t} \\ = y (a_{2} - b_{2} y - c_{2} x) + x (a_{1} - b_{1} x - c_{1} y) \\ = {(M - x) [a_{2} - b_{2} (M - x) - c_{2} x] + x [a_{1} - b_{1} x - c_{1} (M - x)] |}_{l = 0} . \end{array}$

显然，当M充分大时， ${\frac{d l}{d t} |}_{l = 0} < 0$ ，因此系统(2)是有界的。

我们知道了竞争系统(1)是有界的，然后考虑在此基础上添加寨卡病毒项

${\begin{cases} \frac{d y}{d t} = y (a_{2} - b_{2} y - c_{2} x) - r_{1} y z, \\ \frac{d z}{d t} = B + r_{2} y z - d z . \end{cases}$

令

$L = y + \frac{r_{1}}{r_{2}} z,$

我们有

$\begin{matrix} \frac{d L}{d t} = \frac{d y}{d t} + \frac{r_{1}}{r_{2}} \frac{d z}{d t} \\ = y (a_{2} - b_{2} y - c_{2} x) - r_{1} y z + \frac{r_{1}}{r_{2}} (B + r_{2} y z - d z) \\ = y (a_{2} - b_{2} y - c_{2} x) + \frac{r_{1} B}{r_{2}} - \frac{r_{1}}{r_{2}} d z \\ \leq y (a_{2} - m M) + \frac{r_{1} B}{r_{2}} - \frac{r_{1}}{r_{2}} d z \\ = \frac{r_{1} B}{r_{2}} - n (y + \frac{r_{1}}{r_{2}} z) = \frac{r_{1} B}{r_{2}} - n L \end{matrix}$

从而有

$\lim_{t \to \infty} \sup (y + \frac{r_{1}}{r_{2}} z) \leq \frac{1}{n} \frac{r_{1} B}{r_{2}} .$

其中

$m = \min {b_{2}, c_{2}}, n = \min {| a_{2} - n m |, d} .$

所以系统(1)是有界的。又由系统(1)的非负性和有界性，我们可知其正不变集为：

$Γ = {(x, y, z) | x + y \leq M, y + \frac{r_{1}}{r_{2}} z \leq \frac{1}{n} \frac{r_{1} B}{r_{2}}} .$

4. 平衡点的存在性与稳定性分析

前面我们已经讨论了系统的非负性和有界性，接下来考虑系统(1)中平衡点的存在性与稳定性。

引理4.1：1) 系统(1)总存在一个平凡平衡点 $E_{0} (0, 0, \frac{d}{B})$ 。

2) 当 $B > \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 时，系统(1)除了存在平凡平衡点 $E_{0} (0, 0, \frac{d}{B})$ ，还存在肿瘤灭绝平衡点 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ 。

3) 当 $B < \frac{d a_{2}}{r_{1}}$ 且 $\frac{a_{1}}{c_{1}} < y_{2} < \min {\frac{a_{2}}{b_{2}}, \frac{d}{r_{2}}}$ 时，除了存在平凡平衡点 $E_{0} (0, 0, \frac{d}{B})$ ，肿瘤灭绝平衡点 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ ，还存在正常细胞灭绝平衡点 $E_{2} (0, y_{2}, \frac{a_{2} - b_{2} y_{2}}{r_{1}})$ ，其中

$y_{2} = \frac{a_{2} r_{2} + b_{2} d - \sqrt{{(a_{2} r_{2} + b_{2} d)}^{2} - 4 r_{2} b_{2} (a_{2} d - B r_{1})}}{2 b_{2} r_{2}}$

4) 当 $B < \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 且 $c_{1} c_{2} < b_{1} b_{2}, a_{1} c_{2} < a_{2} b_{1}, y_{3} < \min {\frac{a_{1}}{c_{1}}, \frac{d}{r_{2}}}$ 时，除了存在平凡平衡点 $E_{0} (0, 0, \frac{d}{B})$ 和肿瘤灭绝平衡点 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ ，还存在正平衡点 $E_{3} (\frac{a_{1} - c_{1} y_{3}}{b_{1}}, y_{3}, \frac{B}{d - r_{2} y_{3}})$ ，其中

$y_{3} = \frac{- h_{2} - \sqrt{h_{2}^{2} - 4 h_{1} h_{3}}}{2 h_{1}},$

$h_{1} = b_{1} b_{2} r_{2} - c_{1} c_{2} r_{2}, h_{2} = c_{1} c_{2} d + a_{1} c_{2} r_{2} - a_{2} b_{1} r_{2} - b_{1} b_{2} d, h_{3} = a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d .$

证明：1)和2)显而易见，接下来我们证明3)和4)。

3) 当 $y > \frac{a_{1}}{c_{1}}$ 时，溶瘤病毒治疗最终失败，有 $x = 0$ 得到 ${\begin{cases} a_{2} - b_{2} y - r_{1} z = 0 \\ B + r_{2} y z - d z = 0 \end{cases}$ 。要使平衡点 $z_{2}$ 存在，由该方程组的第一个式子知， $a_{2} - b_{2} y_{2} > 0$ 则必有 $y_{2} < \frac{a_{2}}{b_{2}}$ ，由方程组的第二个式子知， $r_{2} y_{2} - d < 0$ 则必有 $y_{2} < \frac{d}{r_{2}}$ ，故 $y_{2} < \min {\frac{a_{2}}{b_{2}}, \frac{d}{r_{2}}}$ 。把 $z = \frac{a_{2} - b_{2} y}{r_{1}}$ 代入方程组得到

$r_{2} b_{2} y^{2} - (a_{2} r_{2} + b_{2} d) y + a_{2} d - B r_{1} = 0.$

不妨记

$f (y) = r_{2} b_{2} y^{2} - (a_{2} r_{2} + b_{2} d) y + a_{2} d - B r_{1},$

由于判别式 $Δ = {(a_{2} r_{2} + b_{2} d)}^{2} - 4 r_{2} b_{2} (a_{2} d - B r_{1}) = {(a_{2} r_{2} - b_{2} d)}^{2} + 4 r_{2} b_{2} B r_{1} > 0$ ，故方程有两个不同的根，设方程的两个根分别为 $y_{1}^{*}, y_{2}^{*}$ ，则 $y_{1}^{*} + y_{2}^{*} = \frac{a_{2} r_{2} + b_{2} d}{r_{2} b_{2}}$ 。

若 $B < \frac{a_{2} d}{r_{1}}$ ，则 $y_{1}^{*} y_{2}^{*} = \frac{a_{2} d - B r_{1}}{r_{2} b_{2}}$ ，即进一步假设 $\frac{a_{2}}{b_{2}} \leq \frac{d}{r_{2}}$ ，则函数 $f (y)$ 的对称轴 $y = \frac{1}{2} (\frac{a_{2}}{b_{2}} + \frac{d}{r_{2}}) \leq \frac{a_{2}}{b_{2}}$ 。

又

$f (0) = a_{2} d - B r_{1} > 0,$

$f (\frac{a_{2}}{b_{2}}) = r_{2} b_{2} {(\frac{a_{2}}{b_{2}})}^{2} - (a_{2} r_{2} + b_{2} d) \frac{a_{2}}{b_{2}} + a_{2} d - B r_{1} = \frac{r_{2} a_{2}^{2}}{b_{2}} - \frac{a_{2}^{2} r_{2}}{b_{2}} - a_{2} d + a_{2} d - B r_{1} = - B r_{1} < 0.$

故 $f (y)$ 在 $(0, \frac{a_{2}}{b_{2}})$ 有一实数根。

同理，假设 $\frac{a_{2}}{b_{2}} \geq \frac{d}{r_{2}}$ ，则函数 $f (y)$ 的对称轴 $y = \frac{1}{2} (\frac{a_{2}}{b_{2}} + \frac{d}{r_{2}}) \leq \frac{d}{r_{2}}$ ，又 $f (0) = a_{2} d - B r_{1} > 0$ ，

$f (\frac{d}{r_{2}}) = r_{2} b_{2} {(\frac{d}{r_{2}})}^{2} - (a_{2} r_{2} + b_{2} d) \frac{d}{r_{2}} + a_{2} d - B r_{1} = \frac{b_{2} d^{2}}{r_{2}} - \frac{d^{2} b_{2}}{r_{2}} - a_{2} d + a_{2} d - B r_{1} = - B r_{1} < 0.$

故 $f (y)$ 在 $(0, \frac{d}{r_{2}})$ 有一实数根。若 $B \geq \frac{a_{2} d}{r_{1}}$ ，此时有 $f (0) = a_{2} d - B r_{1} < 0$ ，且 $f (\frac{a_{2}}{b_{2}}) < 0, f (\frac{d}{r_{2}}) < 0$ ，故 $f (y)$ 在 $(0, \frac{a_{2}}{b_{2}})$ 或 $(0, \frac{d}{r_{2}})$ 均无解。由以上讨论可知，当满足 $B < \frac{d}{r_{1}} a_{2}$ 且 $\frac{a_{1}}{c_{1}} < y_{2} < \min {\frac{a_{2}}{b_{2}}, \frac{d}{r_{2}}}$ 时，系统(1)存在正常细胞灭绝平衡点 $E_{2} (0, y_{2}, \frac{a_{2} - b_{2} y_{2}}{r_{1}})$ ，其中

$y_{2} = \frac{a_{2} r_{2} + b_{2} d - \sqrt{{(a_{2} r_{2} + b_{2} d)}^{2} - 4 r_{2} b_{2} (a_{2} d - B r_{1})}}{2 b_{2} r_{2}} .$

4) 由 ${\begin{cases} a_{1} - b_{1} x - c_{1} y = 0 \\ a_{2} - b_{2} y - c_{2} x - r_{1} z = 0 \\ B + r_{2} y z - d z = 0 \end{cases}$ 可知 ${\begin{cases} x = \frac{a_{1} - c_{1} y}{b_{1}} \\ z = \frac{B}{d - r_{2} y} \end{cases}$ ，要使平衡点 $x_{3}, z_{3}$ 存在，则必有 $a_{1} - c_{1} y_{3} > 0$ 且 $d - r_{2} y_{3} > 0$ 。即 ${\begin{cases} y_{3} < \frac{a_{1}}{c_{1}} \\ y_{3} < \frac{d}{r_{2}} \end{cases}$ ，故 $y_{3} < \min {\frac{a_{1}}{c_{1}}, \frac{d}{r_{2}}}$ 。接下来讨论 $y_{3}$ 平衡点 $y_{3}$ 满足方程

$(b_{1} b_{2} r_{2} - c_{1} c_{2} r_{2}) y_{3}^{2} + (c_{1} c_{2} d + a_{1} c_{2} r_{2} - a_{2} b_{1} r_{2} - b_{1} b_{2} d) y_{3} + a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d = 0$

我们令

$\begin{array}{l} h_{1} = b_{1} b_{2} r_{2} - c_{1} c_{2} r_{2}, h_{2} = c_{1} c_{2} d + a_{1} c_{2} r_{2} - a_{2} b_{1} r_{2} - b_{1} b_{2} d, \\ h_{3} = a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d . \end{array}$

不妨记

$f (y) = (b_{1} b_{2} r_{2} - c_{1} c_{2} r_{2}) y^{2} + (c_{1} c_{2} d + a_{1} c_{2} r_{2} - a_{2} b_{1} r_{2} - b_{1} b_{2} d) y + (a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d),$

由于 $0 < y_{3} < \min {\frac{a_{1}}{c_{1}}, \frac{d}{r_{2}}}$ ，故二次函数 $f (y)$ 只能是开口向上与x轴交2个正根或开口向下与x轴交2个正根的情况。

① 当 $c_{1} c_{2} < b_{1} b_{2}, a_{1} c_{2} < a_{2} b_{1}$ 且 $0 < B < \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 时，则 $h_{1} > 0, h_{2} < 0, h_{3} > 0$ ，进一步假设 $\frac{a_{1}}{c_{1}} \leq \frac{d}{r_{2}}$ ，则函数 $f (y)$ 的对称轴

$y = \frac{1}{2} (\frac{c_{1} c_{2} d + a_{1} c_{2} r_{2} - a_{2} b_{1} r_{2} - b_{1} b_{2} d}{(c_{1} c_{2} - b_{1} b_{2}) r_{2}}) = \frac{1}{2} (\frac{d}{r_{2}} + \frac{a_{1} c_{2} - a_{2} b_{1}}{c_{1} c_{2} - b_{1} b_{2}}) \leq \frac{a_{1}}{c_{1}} .$

$\begin{matrix} f (\frac{a_{1}}{c_{1}}) = (b_{1} b_{2} r_{2} - c_{1} c_{2} r_{2}) {(\frac{a_{1}}{c_{1}})}^{2} + (c_{1} c_{2} d + a_{1} c_{2} r_{2} - a_{2} b_{1} r_{2} - b_{1} b_{2} d) \frac{a_{1}}{c_{1}} \\ + (a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d) \\ = b_{1} d (a_{2} - \frac{a_{1} b_{2}}{c_{1}}) + b_{1} r_{2} \frac{a_{1}}{c_{1}} (\frac{a_{1} b_{2}}{c_{1}} - a_{2}) - r_{1} b_{1} B \\ = b_{1} (\frac{a_{1} b_{2}}{c_{1}} - a_{2}) (r_{2} \frac{a_{1}}{c_{1}} - d) - r_{1} b_{1} B . \end{matrix}$

由 $\frac{a_{1}}{c_{1}} \leq \frac{d}{r_{2}}$ ，得 $\frac{r_{2} a_{1}}{c_{1}} - d < 0$ ，由 $\frac{1}{2} (\frac{d}{r_{2}} + \frac{a_{1} c_{2} - a_{2} b_{1}}{c_{1} c_{2} - b_{1} b_{2}}) \leq \frac{a_{1}}{c_{1}}$ 且 $\frac{a_{1}}{c_{1}} \leq \frac{d}{r_{2}}$ ，得 $\frac{a_{1} b_{2}}{c_{1}} - a_{2} > 0$ 。所以有 $f (\frac{a_{1}}{c_{1}}) < 0$ 。

又 $0 < B < \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ ，因此 $f (0) = a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d > 0$ 。故 $f (y)$ 在 $(0, \frac{a_{1}}{c_{1}})$ 有实数根。

同理，假设 $\frac{a_{1}}{c_{1}} \geq \frac{d}{r_{2}}$ ，则函数 $f (y)$ 的对称轴

$y = \frac{1}{2} \frac{c_{1} c_{2} d + a_{1} c_{2} r_{2} - a_{2} b_{1} r_{2} - b_{1} b_{2} d}{(c_{1} c_{2} - b_{1} b_{2}) r_{2}} = \frac{1}{2} (\frac{d}{r_{2}} + \frac{a_{1} c_{2} - a_{2} b_{1}}{c_{1} c_{2} - b_{1} b_{2}}) \leq \frac{d}{r_{2}},$

$\begin{matrix} f (\frac{d}{r_{2}}) = (b_{1} b_{2} r_{2} - c_{1} c_{2} r_{2}) {(\frac{d}{r_{2}})}^{2} + (c_{1} c_{2} d + a_{1} c_{2} r_{2} - a_{2} b_{1} r_{2} - b_{1} b_{2} d) \frac{d}{r_{2}} \\ + (a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d) \\ = - r_{1} b_{1} B < 0. \end{matrix}$

又 $0 < B < \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ ，因此 $f (0) = a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d > 0$ 。故 $f (y)$ 在 $(0, \frac{d}{r_{2}})$ 有实数根。

② 当 $c_{1} c_{2} > b_{1} b_{2}$ 且 $B > \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 时， $h_{1} < 0, h_{3} < 0$ ，则

$f (0) = a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d < 0.$

若 $\frac{a_{1}}{c_{1}} \leq \frac{d}{r_{2}}$ ，则函数 $f (y)$ 的对称轴

$\begin{matrix} f (\frac{a_{1}}{c_{1}}) = (b_{1} b_{2} r_{2} - c_{1} c_{2} r_{2}) {(\frac{a_{1}}{c_{1}})}^{2} + (c_{1} c_{2} d + a_{1} c_{2} r_{2} - a_{2} b_{1} r_{2} - b_{1} b_{2} d) \frac{a_{1}}{c_{1}} + (a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d) \\ = b_{1} d (a_{2} - \frac{a_{1} b_{2}}{c_{1}}) + b_{1} r_{2} \frac{a_{1}}{c_{1}} (\frac{a_{1} b_{2}}{c_{1}} - a_{2}) - r_{1} b_{1} B \\ = b_{1} (\frac{a_{1} b_{2}}{c_{1}} - a_{2}) (r_{2} \frac{a_{1}}{c_{1}} - d) - r_{1} b_{1} B < 0. \end{matrix}$

即 $f (y)$ 在 $(0, \frac{a_{1}}{c_{1}})$ 无实根。

若 $\frac{a_{1}}{c_{1}} \geq \frac{d}{r_{2}}$ ，则函数 $f (y)$ 的对称轴

$\begin{matrix} f (\frac{d}{r_{2}}) = (b_{1} b_{2} r_{2} - c_{1} c_{2} r_{2}) {(\frac{d}{r_{2}})}^{2} + (c_{1} c_{2} d + a_{1} c_{2} r_{2} - a_{2} b_{1} r_{2} - b_{1} b_{2} d) \frac{d}{r_{2}} + (a_{2} b_{1} d - r_{1} b_{1} B - a_{1} c_{2} d) \\ = - r_{1} b_{1} B < 0. \end{matrix}$

即 $f (y)$ 在 $(0, \frac{d}{r_{2}})$ 无实根。因此，当 $B < \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 且 $c_{1} c_{2} < b_{1} b_{2}, a_{1} c_{2} < a_{2} b_{1}, y_{3} < \min {\frac{a_{1}}{c_{1}}, \frac{d}{r_{2}}}$ 时，系统(1)存在一正平衡点 $E_{3} (\frac{a_{1} - c_{1} y_{3}}{b_{1}}, y_{3}, \frac{B}{d - r_{2} y_{3}})$ ，其中 $y_{3} = \frac{- h_{2} - \sqrt{h_{2}^{2} - 4 h_{1} h_{3}}}{2 h_{1}}$ 。

下面研究系统(1)中平衡点的稳定性，记平衡点E的雅可比矩阵为 $J (E)$ ，则

$J (E) = (\begin{matrix} a_{1} - 2 b_{1} x - c_{1} y & - c_{1} x & 0 \\ - c_{2} y & a_{2} - 2 b_{2} y - c_{2} x - r_{1} z & - r_{1} y \\ 0 & r_{2} z & r_{2} y - d \end{matrix}) .$

定理4.1：系统(1)的平凡平衡点 $E_{0} (0, 0, \frac{B}{d})$ 是不稳定的。

证明：由 $J (E)$ 得

$J (E_{0}) = (\begin{matrix} a_{1} & 0 & 0 \\ 0 & a_{2} - \frac{r_{1} B}{d} & 0 \\ 0 & \frac{r_{2} B}{d} & - d \end{matrix}) .$

其对应的特征方程为

$(λ - a_{1}) (λ - a_{2} + \frac{r_{1} B}{d}) (λ + d) = 0.$

显然，方程有一个特征根 $λ_{1} = a_{1} > 0$ ，所以平凡平衡点 $E_{0} (0, 0, \frac{B}{d})$ 是不稳定的。

由于我们的目的是想要寻找合适的药物投放量B，使得在一定条件下脑肿瘤细胞灭绝。因此，将系统(1)在肿瘤灭绝平衡点 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ 处线性化，得到以下定理：

定理4.2：当 $B > \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 时，系统(1)中肿瘤灭绝平衡点 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ 是局部渐近稳定的，当 $B < \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 时，肿瘤灭绝平衡点 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ 是不稳定的。

证明：由 $J (E)$ 得

$J (E_{1}) = (\begin{matrix} - a_{1} & - \frac{a_{1} c_{1}}{b_{1}} & 0 \\ 0 & a_{2} - \frac{a_{1} c_{2}}{b_{1}} - \frac{r_{1} B}{d} & 0 \\ 0 & \frac{r_{2} B}{d} & - d \end{matrix}) .$

特征方程为

$(λ + a_{1}) (λ - a_{2} + \frac{a_{1} c_{2}}{b_{1}} + \frac{r_{1} B}{d}) (λ + d) = 0.$

解得特征根

$λ_{1} = - a_{1}, λ_{2} = a_{2} - \frac{a_{1} c_{2}}{b_{1}} - \frac{r_{1} B}{d}, λ_{3} = - d .$

当 $B > \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 时，特征根 $λ_{2} < 0$ ，又由于 $λ_{1} < 0, λ_{3} < 0$ ，故肿瘤灭绝平衡点 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ 是局部渐近稳定的。此外，当 $B < \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 时，显然有特征根 $λ_{2} > 0$ ，从而肿瘤灭绝平衡 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ 是不稳定的。

定理4.3：当 $B > \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 时，系统(1)中肿瘤灭绝平衡点 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ 是全局渐近稳定的。

证明：我们知道，当肿瘤细胞最终灭绝时，有 $y \to 0$ ，考虑系统(1)的渐近自治极限系统

${\begin{cases} \frac{d x}{d t} = x (a_{1} - b_{1} x), \\ \frac{d z}{d t} = B - d z . \end{cases}$ (3)

令方程(3)右端等于零，得到两个平衡点 $(0, \frac{B}{d})$ 和 $(\frac{a_{1}}{b_{1}}, \frac{B}{d})$ 。显然 $(\frac{a_{1}}{b_{1}}, \frac{B}{d})$ 是局部渐近稳定的，平衡点 $(0, \frac{B}{d})$ 是不稳定的。对系统(3)取Dulac函数 $D_{1} = \frac{1}{x z}$ ，则

$\frac{\frac{1}{x z} (a_{1} x - b_{1} x^{2})}{\partial x} + \frac{\frac{1}{x z} (B - d z)}{\partial z} = - \frac{b_{1}}{z} - \frac{B}{x z^{2}} < 0.$

这意味着平衡点 $(\frac{a_{1}}{b_{1}}, \frac{B}{d})$ 外围不存在闭轨线，故平衡点 $(\frac{a_{1}}{b_{1}}, \frac{B}{d})$ 在极限渐近自治系统(3)是全局渐近稳定的。又由定理2可知，肿瘤灭绝平衡点 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ 是局部渐近稳定的，因而肿瘤灭绝平衡点 $E_{1} (\frac{a_{1}}{b_{1}}, 0, \frac{B}{d})$ 是全局渐近稳定的。

由该定理可知，当 $B > \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 时，脑肿瘤细胞将会灭绝，正常细胞能够持续生存，趋于一常数值 $\frac{a_{1}}{b_{1}}$ 。这意味着，至少添加药物补充量 $B_{0} = \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 可以清除脑肿瘤细胞，减轻患者痛苦，提高脑癌患者生存几率。

下面讨论正常细胞灭绝平衡点 $E_{2} (0, y_{2}, \frac{a_{2} - b_{2} y_{2}}{r_{1}})$ 的稳定性，得到以下定理：

定理4.4：当 $B < \frac{d}{r_{1}} a_{2}$ 且 $\frac{a_{1}}{c_{1}} < y_{2} < \min {\frac{a_{2}}{b_{2}}, \frac{d}{r_{2}}}$ 时，正常细胞灭绝平衡点 $E_{2} (0, y_{2}, \frac{a_{2} - b_{2} y_{2}}{r_{1}})$ 是全局渐近稳定的。

证明：由 $J (E)$ 得

$J (E_{2}) = (\begin{matrix} a_{1} - c_{1} y_{2} & 0 & 0 \\ - c_{2} y_{2} & - b_{2} y_{2} & - r_{1} y_{2} \\ 0 & r_{2} \frac{a_{2} - b_{2} y_{2}}{r_{1}} & r_{2} y_{2} - d \end{matrix}) .$

其对应的特征方程为：

$(λ - a_{1} + c_{1} y_{2}) [(λ + b_{2} y_{2}) (λ - r_{2} y_{2} + d) + r_{2} y_{2} (a_{2} - b_{2} y_{2})] = 0.$

由于 $y_{2} > \frac{a_{1}}{c_{1}}$ ，故特征根 $a_{1} - c_{1} y_{2} < 0$ 。 $λ_{2}$ 和 $λ_{3}$ 满足方程

$λ^{2} + (b_{2} y_{2} + d - r_{2} y_{2}) λ + (b_{2} d y_{2} + a_{2} r_{2} y_{2} - 2 b_{2} r_{2} y_{2}^{2}) = 0.$

由 $y_{2} < \frac{d}{r_{2}}$ 且 $y_{2} < \frac{a_{2}}{b_{2}}$ 得到

$λ_{2} + λ_{3} = r_{2} y_{2} - b_{2} y_{2} - d < 0,$

$λ_{2} λ_{3} = b_{2} d y_{2} + a_{2} r_{2} y_{2} - 2 b_{2} r_{2} y_{2}^{2} = y_{2} [b_{2} (d - r_{2} y_{2}) + r_{2} (a_{2} - b_{2} y_{2})] > 0.$

故 $λ_{2} < 0, λ_{3} < 0$ 。因此，当 $B < \frac{d}{r_{1}} a_{2}$ 且 $\frac{a_{1}}{c_{1}} < y_{2} < \min {\frac{a_{2}}{b_{2}}, \frac{d}{r_{2}}}$ 时正常细胞灭绝平衡点 $E_{2} (0, y_{2}, \frac{a_{2} - b_{2} y_{2}}{r_{1}})$ 是局部渐近稳定的。

下证该平衡点的全局稳定性。当 $x \to 0$ 时，系统(1)变为极限系统

${\begin{cases} \frac{d y}{d t} = y (a_{2} - b_{2} y - r_{1} z), \\ \frac{d z}{d t} = B + r_{2} y z - d z . \end{cases}$ (4)

令方程(4)右端等于零，我们得到两个平衡点 $(0, \frac{B}{d})$ 和 $(y, \frac{a_{2} - b_{2} y}{r_{1}})$ 。容易知道 $(0, \frac{B}{d})$ 是不稳定的， $(y, \frac{a_{2} - b_{2} y}{r_{1}})$ 是局部渐近稳定的。对系统(4)取Dulac函数 $D_{2} = \frac{1}{y z}$ ，则

$\frac{\frac{1}{y z} y (a_{2} - b_{2} y - r_{1} z)}{\partial y} + \frac{\frac{1}{y z} (B + r_{2} y z - d z)}{\partial z} = - \frac{b_{2}}{z} - \frac{B}{y z^{2}} < 0.$

即平衡点 $(y, \frac{a_{2} - b_{2} y}{r_{1}})$ 外围不存在闭轨线，所以平衡点 $(y, \frac{a_{2} - b_{2} y}{r_{1}})$ 在极限渐近自治系统(4)是全局渐近稳定的。因而正常细胞灭绝平衡点 $E_{2} (0, y_{2}, \frac{a_{2} - b_{2} y_{2}}{r_{1}})$ 是全局渐近稳定的。该定理表明，最终溶瘤病毒治疗失败，这是由于脑肿瘤细胞的无限增值性，对抗肿瘤信号和逃避凋亡等因素作用，而且竞争排斥原理导致脑肿瘤细胞吸收营养比正常细胞要多，所以最终脑肿瘤细胞持续生存，而正常细胞趋于灭绝状态[11]。

前面我们已经证明肿瘤灭绝平衡点与正常细胞灭绝平衡点的全局稳定性，接下来讨论正平衡点的稳定性。

定理4.5：当 $B < \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}}), c_{1} c_{2} < b_{1} b_{2}, a_{1} c_{2} < a_{2} b_{1}, y_{3} < \min {\frac{a_{1}}{c_{1}}, \frac{d}{r_{2}}}$ 时，正平衡点 $E_{3} (\frac{a_{1} - c_{1} y_{3}}{b_{1}}, y_{3}, \frac{B}{d - r_{2} y_{3}})$ 是局部渐近稳定的。

证明：正平衡点 $E_{3} (\frac{a_{1} - c_{1} y_{3}}{b_{1}}, y_{3}, \frac{B}{d - r_{2} y_{3}})$ 在系统(1)的雅可比矩阵为：

$J (E_{3}) = (\begin{matrix} c_{1} y_{3} - a_{1} & - \frac{c_{1} (a_{1} - c_{1} y_{3})}{b_{1}} & 0 \\ - c_{2} y_{3} & a_{2} - 2 b_{2} y_{3} - \frac{c_{2} (a_{1} - c_{1} y_{3})}{b_{1}} - \frac{B r_{1}}{d - r_{2} y_{3}} & - r_{1} y_{3} \\ 0 & \frac{B r_{2}}{d - r_{2} y_{3}} & r_{2} y_{3} - d \end{matrix}) .$

其对应的特征方程为：

$λ^{3} + e_{1} λ^{2} + e_{2} λ + e_{3} = 0.$

其中：

$\begin{array}{l} e_{1} = - [(r_{2} y_{3} - d) + (a_{2} - 2 b_{2} y_{3} - \frac{c_{2} (a_{1} - c_{1} y_{3})}{b_{1}} - \frac{B r_{1}}{d - r_{2} y_{3}}) + (c_{1} y_{3} - a_{1})] \\ = (a_{1} - c_{1} y_{3}) + (d - r_{2} y_{3}) + y_{3} (b_{2} - \frac{c_{1} c_{2}}{b_{1}}) \\ + [\frac{a_{1} c_{2}}{b_{1}} - (a_{2} - b_{2} y_{3} - \frac{B r_{1}}{d - r_{2} y_{3}})] > 0. \end{array}$

$\begin{array}{l} e_{2} = (a_{2} - 2 b_{2} y_{3} - \frac{c_{2} (a_{1} - c_{1} y_{3})}{b_{1}} - \frac{B r_{1}}{d - r_{2} y_{3}}) (r_{2} y_{3} - d) + \frac{B r_{2}}{d - r_{2} y_{3}} r_{1} y_{3} + (c_{1} y_{3} - a_{1}) (r_{2} y_{3} - d) \\ + (a_{2} - 2 b_{2} y_{3} - \frac{c_{2} (a_{1} - c_{1} y_{3})}{b_{1}} - \frac{B r_{1}}{d - r_{2} y_{3}}) (c_{1} y_{3} - a_{1}) + c_{2} y_{3} \frac{c_{1} (a_{1} - c_{1} y_{3})}{b_{1}} \\ = (a_{2} - 2 b_{2} y_{3} - \frac{c_{2} (a_{1} - c_{1} y_{3})}{b_{1}} - \frac{B r_{1}}{d - r_{2} y_{3}}) (r_{2} y_{3} - d + c_{1} y_{3} - a_{1}) \\ + (a_{1} - c_{1} y_{3}) (\frac{c_{1} c_{2} y_{3}}{b_{1}} - r_{2} y_{3} + d) + \frac{B r_{2}}{d - r_{2} y_{3}} r_{1} y_{3} \end{array}$

$\begin{array}{l} = [(a_{2} - b_{2} y_{3} - \frac{B r_{1}}{d - r_{2} y_{3}}) - \frac{a_{1} c_{2}}{b_{1}} + y_{3} (\frac{c_{1} c_{2}}{b_{1}} - b_{2})] (r_{2} y_{3} - d + c_{1} y_{3} - a_{1}) \\ + (a_{1} - c_{1} y_{3}) (\frac{c_{1} c_{2} y_{3}}{b_{1}} - r_{2} y_{3} + d) + \frac{B r_{2}}{d - r_{2} y_{3}} r_{1} y_{3} > 0. \end{array}$

$\begin{matrix} e_{3} = c_{2} y_{3} c_{1} \frac{a_{1} - c_{1} y_{3}}{b_{1}} (r_{2} y_{3} - d) - (c_{1} y_{3} - a_{1}) (a_{2} - 2 b_{2} y_{3} - \frac{c_{2} (a_{1} - c_{1} y_{3})}{b_{1}} - \frac{B r_{1}}{d - r_{2} y_{3}}) (r_{2} y_{3} - d) \\ - (c_{1} y_{3} - a_{1}) r_{1} y_{3} \frac{B r_{2}}{d - r_{2} y_{3}} \\ = (a_{1} - c_{1} y_{3}) [c_{2} y_{3} c_{1} \frac{r_{2} y_{3} - d}{b_{1}} + (a_{2} - 2 b_{2} y_{3} - \frac{c_{2} (a_{1} - c_{1} y_{3})}{b_{1}} - \frac{B r_{1}}{d - r_{2} y_{3}}) (r_{2} y_{3} - d) + r_{1} y_{3} \frac{B r_{2}}{d - r_{2} y_{3}}] \\ = (a_{1} - c_{1} y_{3}) [(r_{2} y_{3} - d) (\frac{c_{2} y_{3} c_{1}}{b_{1}} + a_{2} - 2 b_{2} y_{3} - \frac{c_{2} (a_{1} - c_{1} y_{3})}{b_{1}} - \frac{B r_{1}}{d - r_{2} y_{3}}) + r_{1} y_{3} \frac{B r_{2}}{d - r_{2} y_{3}}] \end{matrix}$

$\begin{matrix} = (a_{1} - c_{1} y_{3}) [(r_{2} y_{3} - d) (a_{2} - b_{2} y_{3} - \frac{B r_{1}}{d - r_{2} y_{3}} - b_{2} y_{3} + \frac{c_{1} c_{2} y_{3}}{b_{1}}) + r_{1} y_{3} \frac{B r_{2}}{d - r_{2} y_{3}}] \\ = (a_{1} - c_{1} y_{3}) [(r_{2} y_{3} - d) (\frac{c_{2} (a_{1} - c_{1} y_{3})}{b_{1}} - b_{2} y_{3} + \frac{c_{1} c_{2} y_{3}}{b_{1}}) + r_{1} y_{3} \frac{B r_{2}}{d - r_{2} y_{3}}] \\ > (a_{1} - c_{1} y_{3}) [(r_{2} y_{3} - d) (\frac{a_{1} c_{2}}{b_{1}} - \frac{b_{2} a_{1}}{c_{1}}) + r_{1} y_{3} \frac{B r_{2}}{d - r_{2} y_{3}}] > 0. \end{matrix}$

故特征方程的所有特征根均具有负实部，因而正平衡点 $E_{3} (\frac{a_{1} - c_{1} y_{3}}{b_{1}}, y_{3}, \frac{B}{d - r_{2} y_{3}})$ 是局部渐近稳定的。

5. 数值模拟

在本节中，为了验证以上结论，我们利用数学软件MATLAB进行数值模拟，参数值仅供参考。现在考虑在不同的竞争状态下，添加适当的寨卡病毒药物补充量，得到不同的平衡点稳定性，取 $a_{1} = 3, a_{2} = 2, b_{1} = 0.5, b_{2} = 0.5, c_{1} = 0.2, c_{2} = 0.3, r_{1} = 0.4, r_{2} = 0.5, B = 2, d = 0.7$ 时， $B > \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}}) = 0.35$ ，最终得到肿瘤灭绝平衡点 $E_{1} (6, 0, 2.8571)$ 是全局渐近稳定的(如图1所示)。

取 $a_{1} = 1, a_{2} = 2, b_{1} = 0.5, b_{2} = 1.5, c_{1} = 1.5, c_{2} = 0.5, r_{1} = 0.4, r_{2} = 0.5, B = 0.2, d = 0.7$ 时， $B < \frac{d}{r_{1}} a_{2} = 3.5$ ，最终得到正常细胞灭绝平衡点 $E_{2} (0, 1.0383, 1.1061)$ 是全局渐近稳定的(如图2所示)。

取 $a_{1} = 1, a_{2} = 2, b_{1} = 0.5, b_{2} = 1, c_{1} = 0.4, c_{2} = 0.5, r_{1} = 0.4, r_{2} = 0.5, B = 1, d = 0.7$ 时， $B < \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}}) = 1.75$ ，最终得到正平衡点 $E_{3} (1.7032, 0.3710, 1.9436)$ 是局部渐近稳定的(如图3所示)。

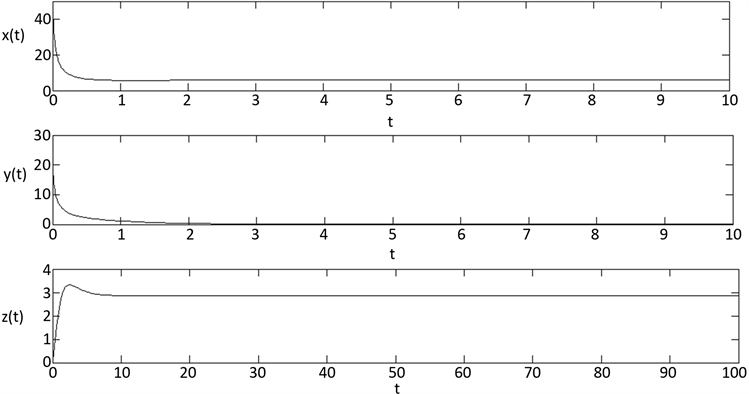
Figure 1. The Stability of tumor extinction equilibrium E₁

图1. 肿瘤灭绝平衡点E₁的稳定性

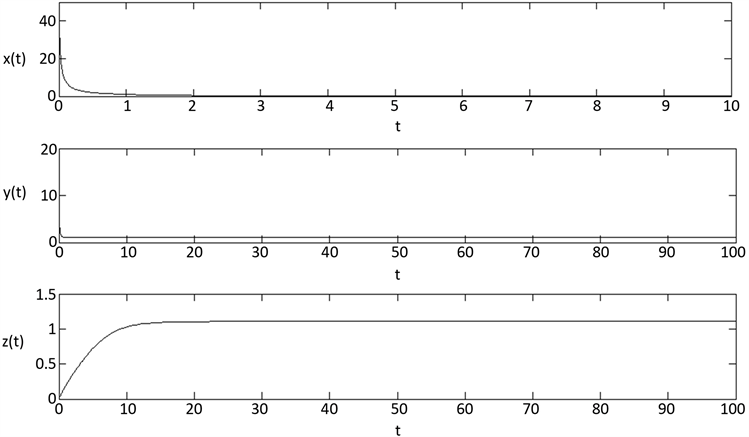
Figure 2. The Stability of normal cell extinction equilibrium E₂

图2. 正常细胞灭绝平衡点E₂的稳定性

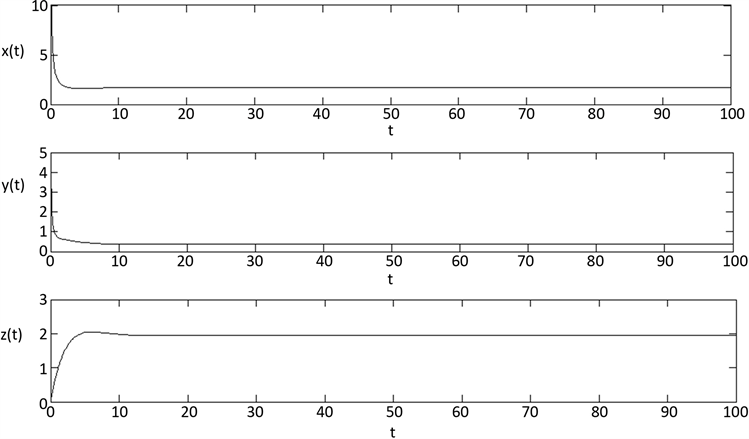
Figure 3. The Stability of the positive equilibrium E₃

图3. 正平衡点E₃的稳定性

6. 结论

本文建立了基于正常细胞和脑肿瘤细胞相互竞争营养的寨卡病毒溶瘤治疗模型，首先考虑了系统的非负性和有界性，讨论了平衡点的存在性和稳定性。若药物补充量B满足参数 $B > \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}})$ 时，肿瘤灭绝平衡点是全局渐近稳定的，即肿瘤最终细胞灭绝，溶瘤治疗效果最佳；若 $B < \frac{d}{r_{1}} a_{2}$ 且 $\frac{a_{1}}{c_{1}} < y_{2} < \min {\frac{a_{2}}{b_{2}}, \frac{d}{r_{2}}}$ 时，正常细胞灭绝平衡点是全局渐近稳定的；若 $B < \frac{d}{r_{1}} (a_{2} - \frac{a_{1} c_{2}}{b_{1}}), c_{1} c_{2} < b_{1} b_{2}, a_{1} c_{2} < a_{2} b_{1}, y_{3} < \min {\frac{a_{1}}{c_{1}}, \frac{d}{r_{2}}}$ 时，正常细胞，脑癌细胞与寨卡病毒三者共存达到平衡态。由以上讨论，我们可以通过添加不同的药物补充量来改变治疗效果，这对控制病情起关键作用，为理论上预防和控制脑癌提供了一个有效的方法。

基金项目

本文得到国家自然科学基金(11771104)资助，在此表示感谢!

文章引用

杨婷梅,刘建. 寨卡病毒溶瘤治疗脑癌的数学模型动力学分析
Dynamic Analysis of Mathematical Model in Brain Cancer Treatment by Zika Virus Oncolysis[J]. 应用数学进展, 2019, 08(02): 277-291. https://doi.org/10.12677/AAM.2019.82032

参考文献

1. Markert, J.M., Medlock, M.D., Rabkin, S.D., et al. (2000) Conditionally Replicating Herpes Simplex Virus Mutant, G207 for the Treatment of Malignant Glioma: Results of Aphase 1 Trial. Gene Therapy, 7, 867-874. https://doi.org/10.1038/sj.gt.3301205

2. Khuri, F.R., Nemunaitis, J., Ganly, I., et al. (2000) A Controlled Trial of Intratumoral ONYX-015, a Selectively-Replicating Adenovirus, in Combination with Cisplatin and 5-Fluorouracil in Patients with Recurrent Head and Neck Cancer. Nature Medicine, 6, 879-885. https://doi.org/10.1038/78638

3. Csatary, L.K., Goszonyi, G., Szeberenyi, J., et al. (2004) MTH-68/H Oncolytic Viral Treatment in Human High-Grade Gliomas. Journal of Neuro-Oncology, 67, 83-93. https://doi.org/10.1023/B:NEON.0000021735.85511.05

4. Garber, K. (2006) China Approves World’s First Oncolytic Virus Therapy for Cancer Treatment. Journal of the National Cancer Institute, 98, 298-300. https://doi.org/10.1093/jnci/djj111

5. Lin, Y., Zhang, H., Liang, J., et al. (2014) Identification and Characteri-zation of Alphavirus M1 as a Selective Oncolytic Virus Targeting ZAP-Defective Human Cancers. Proceedings of the National Academy of Sciences of USA, 111, E4504-E4512. https://doi.org/10.1073/pnas.1408759111

6. Andtbacka, R.H., Kaufman, H.L., Collichio, F., et al. (2015) Talimogene Laherparepvec Improves Durable Response Rate in Patients with Advanced Melanoma. Journal of Clinical Oncology, 33, 2780-2788. https://doi.org/10.1200/JCO.2014.58.3377

7. 朱贵东, 刘福生. 溶瘤病毒治疗脑胶质瘤新进展[J]. 中华神经外科杂志, 2010, 26(5): 472-474.

8. 于春泳, 杨辉. 神经干细胞与脑胶质瘤干细胞[J]. 中国组织工程研究与临床康复, 2009, 13(6): 1163-1166.

9. 陈奇, 秦成峰. 寨卡病毒可作为溶瘤病毒特异杀伤胶质瘤干细胞[J]. 中国科学: 生命科学, 2018, 48(10): 1126-1127.

10. Zhu, Z., Gorman, M.J., McKenzie, L.D., et al. (2017) Zika Virus Has Oncolytic Activity against Glioblastoma Stem Cells. Journal of Experimental Medicine, 214, 2843-2857. https://doi.org/10.1084/jem.20171093

11. 张硕, 李德新. 寨卡病毒和寨卡病毒病[J]. 病毒学报, 2016, 32(1): 121-127.

12. 王子子. 关于肿瘤溶瘤病毒疗法的数学模型及其分析[D]: [博士学位论文]. 广州: 广州大学, 2017: 17-91.

期刊菜单