Advances in Applied Mathematics
Vol.
09
No.
03
(
2020
), Article ID:
34629
,
10
pages
10.12677/AAM.2020.93045
TDOA Localization Algorithm Based on Lagrange Constraint Factor to Modify the Initial Value of Iteration
Yuqin Su, Xiaoning Fu, Na Zhang
Xidian University, Xi’an Shaanxi

Received: Feb. 29th, 2020; accepted: Mar. 13th, 2020; published: Mar. 20th, 2020

ABSTRACT
For the TDOA positioning method, different algorithms determine different positioning accuracy, and the traditional Taylor series expansion method has a strong dependence on the suitability of the initial value selection. In order to improve the positioning accuracy, this paper proposes a method to correct the initial position error by introducing the Lagrange constraint factor on the basis of Taylor-series estimation. Simulation experiment I shows that under the same simulation conditions, the optimal positioning accuracy of the traditional Taylor series expansion method is lower than that of the Chan algorithm. Simulation experiment II shows that when the number of satellite observation platform networks is 4 and 6 respectively, the positioning accuracy of the modified algorithm proposed in this paper is better than the traditional Chan algorithm and Taylor algorithm.
Keywords:TDOA, Constraint Factor, Taylor-Series Estimation

基于Lagrange约束因子修正迭代初值的TDOA定位算法
苏煜琴,付小宁,张娜
西安电子科技大学,陕西 西安

收稿日期:2020年2月29日;录用日期:2020年3月13日;发布日期:2020年3月20日

摘 要
对于TDOA定位法,不同的解算算法决定了不同的定位精度,传统的Taylor级数展开法对于初值选取的合适与否依赖性较强。为提高定位精度,本文在Taylor级数展开法的基础上提出了一种引入Lagrange约束因子修正初始位置误差的解算方法。仿真实验I表明,在同等仿真条件下,传统Taylor级数展开法的最优定位精度次于Chan算法的最优定位精度。仿真实验II表明,在星载观测平台组网个数分别为4、6时,本文提出的修正算法定位精度都优于传统的Chan算法、Taylor算法。
关键词 :TDOA,约束因子,Taylor级数展开法

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,随着通信技术和电磁信号等科学技术的发展与研究,资源争夺的领地已经不仅仅局限于海洋与陆地,如何掌握空中制导权已经成了各国军备竞赛的重要争夺单元。基于单星载观测平台的定位系统虽然机动性能好,但定位精度往往达不到1 km [1]。增加观测平台可以得到更多的定位参数信息,如到达时间差(Time Difference of Arrival, TDOA) [2] 、到达频率、到达频率差(Frequency Difference of Arrival, FDOA) [3] 、多普勒频率和多普勒频率变化率 [4] 等,其中TDOA定位法是使用最广泛的定位算法。
TDOA定位方程的解算方式与定位精度有直接关系 [5]。最早的定位算法是1976年Foy等人提出的Taylor级数展开法 [6],本质上是一种迭代算法,类似的,还有利用Newton迭代法进行位置求解,迭代算法的优点是定位精度高 [7],但是缺点迭代算法计算复杂,且需要选取合适的目标位置初始值,因此如何优化上述算法十分有研究意义。除了迭代法,还有以Y.T. Chan提出的Chan算法 [8] 为代表的解析法。此外,还有一种闭式解法思想,代表算法有球面相交法(SX) [9] 、平面相交法(PX) [10] 和球面插值法(SI) [11],尽管这些算法都可以求得目标的位置解,但是闭式解法有一个共同的缺点,定位性能无法达到克拉美罗下界 [12]。
2. TDOA定位原理
到达时间差(Time Difference of Arrival, TDOA)定位法,简称时差定位法。目标到达两个星载观测站的时间先后不同,故而可以得到一个时间差,利用速度距离公式可以确定一个双曲面,空间中三组双曲面相交可以得到一个交点,此交点即为近地辐射源目标。获得三组双曲面,至少需要三个星载观测平台,因此时差定位法对三维空间目标进行定位至少需要三个或三个以上的星载平台来组成定位网络。定位原理图如图1。
假设在地心固定坐标系描述下辐射源目标为 , 均为星载观测平台,为了方便描述,以 为主观测平台,其余观测平台为辅助观测平台,三维坐标表示为 。
以星载观测平台组网个数是四个为例,根据几何关系有:

Figure 1. Schematic diagram of 3D TDOA positioning principle
图1. 三维TDOA定位原理示意图
(1)
将速度距离公式带入式(1)有:
(2)
整理式(1)、式(2)得:
(3)
其中: ,。
解方程组式(3)即可得到近地辐射源的坐标。
3. Chan算法
1994年学者Y.T. Chan提出了一种本质并非迭代法的非线性方程求解算法,该算法本质是解析式法,并且不需要设置初值,计算量也大大降低,于是该算法被命名为Chan算法。
该算法将辐射源目标与星载观测平台之间的距离视为常量,则式(3)可以写为:
(4)
其中: ,,。
假设四个星载观测平台呈不规则分布,不会处于同一水平线上,则有 ,此时辐射源目标的位置的最小二乘解可以由伪逆法求得:
(5)
记式(8)中的
(6)
联立式(8)与式(9)可得近地辐射源目标位置的估计值:
(7)
其中: 。
将式(10)带入式(1)得:
(8)
其中: 。
此时求解辐射源目标的位置解从求解复杂的非线性方程转化为求解一元二次方程,大大降低了计算复杂度,求解过程有以下三种情况:
1) 当判别式 时,式(11)有两解,此时出现了时差定位模糊现象;
2) 当判别式 时,式(11)有一解,此时的解便是辐射源目标的位置解,没有出现时差定位模糊现象;
3) 当判别式 时,式(11)无解,时差定位曲线无交点,定位失效。
当判别式大于等于零时,对该一元二次方程进行求解便得到近地辐射源目标的位置解:
(9)
将式(12)与式(1)、(2)联立即可求得近地辐射源目标的位置。
以上便是Chan算法的解算步骤。但是由以上分析可知Chan算法有可能出现定位模糊甚至无解的情况,此时TDOA定位法的定位结果将受较大影响。
4. Taylor级数展开法
Taylor级数展开法本质上是一种迭代算法,核心思想 [13] 是:将TDOA定位方程按照Taylor级数终值定理展开,并忽略二阶及二阶以上的分量,在开始迭代前为目标位置赋予初值,之后在此基础上进行迭代,在每一次的迭代过程中通过局部最小二乘解(Least Squares, LS)逐渐收敛于辐射源目标位置解。
1) 根据TDOA定位原理,将迭代初始值设为 ,与真实位置的测量误差记为 ,则有如下关系:
(10)
2) 在迭代初始值处按照Taylor级数展开,去除二阶以上高阶分量的同时仅保留一阶分量,得到如下表达式:
(11)
其中: 为TDOA定位法中时间测量误差矩阵; ;
3) 用加权最小二乘法得出初始位置处的最大似然估计:
(12)
其中:Q为TDOA定位法测量误差的协方差矩阵。
4) 设定一个门限精度 :
如果 ,则终止迭代过程,此时可以得出近地辐射源目标最终位置估计值:
(13)
如果
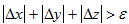 ,则继续执行步骤5)。
,则继续执行步骤5)。
5) 用最新得到估计值的估计值替代上一个估计值,并重复步骤3)和步骤4)。
以上便是Taylor级数展开法的解算步骤。
5. 基于Lagrange约束因子的修正算法
Chan算法计算简单但是有时差模糊现象,该现象严重可导致系统定位功能失效;Taylor算法尽管计算复杂,但每次都能得到确定的位置解,此外初值选取的合适与否对定位结果有直接的影响。随着计算机计算速度的加快,复杂的计算已经变得不再复杂,为此提出一种基于Lagrange约束因子的解算方法。
式(3)转化为矩阵表达形式为:
(14)
其中: ;
;
。
考虑到系统总含有观测噪声及测量误差,故在计算过程加入误差干扰项,用最小二乘法求得位置估计值为:
(15)
其中: 是矩阵 的最小奇异值;I为单位阵; 为误差项。
为了计算方便,将主观测平台所在的位置设为坐标原点,故式(1)的第一行可简化为:
(16)
进一步转化为矩阵表达形式为:
(17)
其中: 。
至此,引入Lagrange数乘因子 ,Lagrange数乘算法 [14] 的思想由Joseph Lagrange在1971年首次提出,用来解决数学解算过程中的最优问题。利用该思想,得到以下约束表达式:
(18)
对 求一阶偏导数并令其为零:
(19)
解上述方程,得:
(20)
联立式(20)和式(23),有:
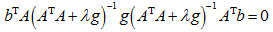 (21)
(21)
为了求解上式,先令 ,其中 , 为矩阵 的特征值,所以有:
(22)
将式(25)带入式(23)整理为矩阵表达形式为:
(23)
其中: ; 。
将矩阵表达形式整理为代数表达形式为:
(24)
解该代数方程便可以得到Lagrange数乘因子 ,将其带入式(23)便可以得到位置解X。
根据位置解X得到误差修正项 的表达式:
(25)
最终得到修正后的位置:
(26)
将修正后的位置作为Taylor展开时的初始值,之后进行Taylor级数展开法,当满足精度要求终止迭代时,本文提出的基于Lagrange约束因子的解算方法解算完成,算法流程图如图2。
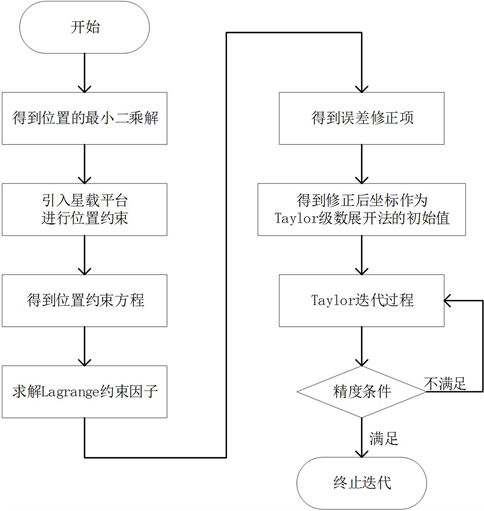
Figure 2. The principle diagram of Lagrange constraint factor correction algorithm
图2. 基于Lagrange约束因子修正算法原理图
6. 实验结果及分析
实验I:星载观测平台数量对不同定位算法精度的影响
各星载观测平台的位置坐标如表1所示,以星载观测平台1的位置为坐标原点,近地辐射源目标的位置为 。TDOA测量误差服从理想高斯噪声环境。
定位精度用均方根误差来评判,计算公式为:
(27)
其中:X为第i次估计的近地辐射源目标位置; 为近地辐射源目标的真实位置; 为采样次数。
由图3、图4可知,Chan算法定位精度比Taylor级数展开法对定位系统中星载观测平台的个数更加敏感,尽管如此Chan算法也可以随着星载观测平台的个数增加得到更好的定位精度,但是当参与定位的星载观测平台个数达到5个及以上时,对定位精度改善不大。Taylor级数展开法的定位精度受星载观测平台的个数的影响不大,当个数达到四个或以上时,定位精度达到最优,并很难随着观测平台的增加而明显提高。就总体而言,Taylor级数展开法的最优定位精度次于Chan算法的最优定位精度。
Table 1. Location distribution of space borne observation platform
表1. 星载观测平台的位置分布

Figure 3. Performance of Chan algorithm under different spaceborne observation platforms
图3. 不同星载观测平台下Chan算法的性能
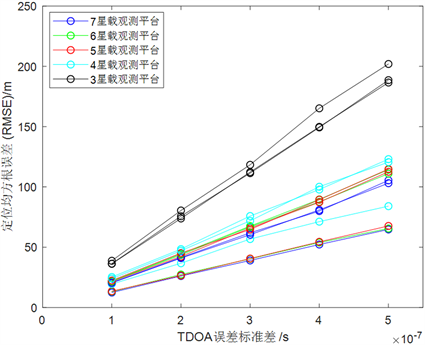
Figure 4. Performance of Taylor algorithm under different spaceborne observation platforms
图4. 不同星载观测平台下Taylor算法的性能
实验II:不同定位算法的性能比较
基于实验I的仿真结果,实验II选择星载观测平台的个数分别为4、6,星载观测平台的位置同实验I。TDOA测量误差服从理想高斯噪声环境。
定位精度用均方误差来评判,计算公式为:
(28)
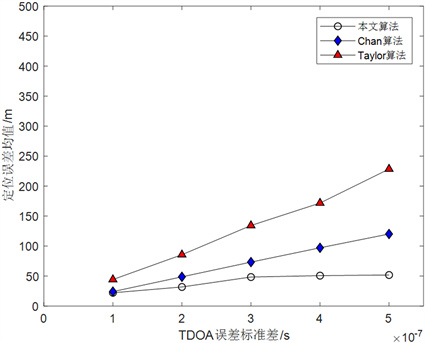
Figure 5. Performance comparison of three positioning algorithms under four spaceborne observation platforms
图5. 四个星载观测平台下三种定位算法性能比较
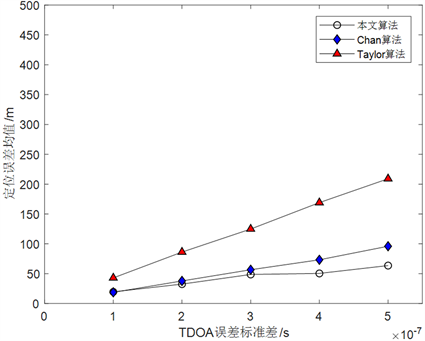
Figure 6. Performance comparison of three positioning algorithms under six spaceborne observation platforms
图6. 六个星载观测平台下三种定位算法性能比较
图5、图6分别给出了同等仿真条件下Taylor级数展开法、Chan算法、本文提出的解算算法在4个星载观测平台、6个星载观测平台下的仿真结果。
由图可知,无论星载观测平台的个数是多少,本文提出的解算算法定位精度最高,Chan算法次之,Taylor级数展开法的定位性能最差,这说明初值的选取对Taylor级数展开法的定位精度有直接影响。本文用Lagrange约束因子修正后的位置值作为Taylor级数展开法的迭代初始值后,定位精度有了明显的提升。
7. 结论
本文提出的基于Lagrange约束因子修正算法引入了Lagrange约束因子,利用星载观测平台位置的已知性作为约束条件,求解出辐射源目标的位置在该约束条件下的修正解,并将修正后的位置作为Taylor级数展开法中的初值。仿真结果表明,传统Taylor级数展开法的最优定位精度次于Chan算法的最优定位精度,而本文提出的Taylor级数展开法修正算法在不同观测平台个数下的定位精度都高于传统的Chan算法、Taylor算法的定位精度。
但是本文仅在高斯噪声环境中做了仿真实验,真实的测量环境的噪声十分复杂,需要进一步探究。基于此,在后续的研究中考虑引入合适的滤波器滤除噪声及误差。同时,如何降低迭代次数,使得估计值快速收敛到目标真实值也是一个重要的研究课题。
文章引用
苏煜琴,付小宁,张 娜. 基于Lagrange约束因子修正迭代初值的TDOA定位算法
TDOA Localization Algorithm Based on Lagrange Constraint Factor to Modify the Initial Value of Iteration[J]. 应用数学进展, 2020, 09(03): 372-381. https://doi.org/10.12677/AAM.2020.93045
参考文献
- 1. Yang, X., Li, J. and Zhang, S. (2014) Ionospheric Correction for Spaceborne Single-Frequency GPS Based on Single Layer Model. Journal of Earth System Science, 123, 767-778. https://doi.org/10.1007/s12040-014-0442-z
- 2. Ankit, J., Pascal, P., Rolland, F., et al. (2018) Accurate Time Difference of Arrival Estimation for HF Radio Broadcast Signals. Microwave and Optical Technology Letters, 60, 1406-1410. https://doi.org/10.1002/mop.31178
- 3. Adamy, D. (2005) Precision Emitter Location by FDOA. The Journal of Electronic Defense, 28, 62-63.
- 4. 刁鸣, 王越. 基于多普勒频率变化率的无源定位算法研究[J]. 系统工程与电子技术, 2006, 28(5): 696-698.
- 5. Boccadoro, M., De, A. and Valigi, P. (2012) TDOA Positioning in NLOS Scenarios by Particle Filtering. Wireless Networks, 18, 579-589. https://doi.org/10.1007/s11276-012-0420-9
- 6. Foy, W.H. (1976) Position-Location Solution by Taylor-Series Estimation. IEEE Transactions on Aerospace and Electronic Systems, 12, 187-194. https://doi.org/10.1109/TAES.1976.308294
- 7. Chernoguz, N. (1995) A Smoothed Newton-Gauss Method with Application to Bearing-Only Position Location. IEEE Transactions on Signal Processing, 43, 2011-2013. https://doi.org/10.1109/78.403366
- 8. Chan, Y., So, H., Lee, B., et al. (2013) Angle of Arrival Localization of an Emitter from Air Platforms. IEEE Canadian Conference of Electrical and Computer Engineering, Regina, 5-8 May 2013, 1-5. https://doi.org/10.1109/CCECE.2013.6567733
- 9. Anna, O. and Alon, A. (2012) An Extended Spheri-cal-Intersection Method for Acoustic Sensor Network Localization with Unknown Propagation Speed. 2012 IEEE 27th Convention of Electrical and Electronics Engineers in Israel, Eilat, 14-17 November 2012.
- 10. Zhang, X., Wu, D., Liu, C., et al. (2012) Analysis on Capacity of Reformed Signalized Plane Intersection. 2012 2nd International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, 1-3 June 2012. https://doi.org/10.1109/RSETE.2012.6260396
- 11. Freeden, W. and T?rnig, W. (2011) On Spherical Spline In-terpolation and Approximation. Mathematical Methods in the Applied Sciences, 3, 551-575. https://doi.org/10.1002/mma.1670030139
- 12. Yacine, A., Julio, C. and Hurd, T. (2009) Portfolio Choice with Jumps: A Closed-Form Solution. Annals of Applied Probability, 19, 556-584. https://doi.org/10.1214/08-AAP552
- 13. 李莉, 邓平, 刘林. Taylor级数展开法定位及其性能分析[J]. 西南交通大学学报, 2002, 37(6): 684-688.
- 14. Annibalem, P., Filos, J. and Naylor, P. (2012) TDOA-Based Speed of Sound Estimation for Air Temperature and Roomgeometry Inference. IEEE Transactions on Audio, and Language Processing, 21, 234-246. https://doi.org/10.1109/TASL.2012.2217130
