Advances in Education
Vol.
09
No.
02
(
2019
), Article ID:
29171
,
4
pages
10.12677/AE.2019.92027
Suggestions on the Measurement of Liquid Viscosity Coefficient
Yun Jia, Jingfeng Wang, Zhihao Zhang, Lei Gao, Yuquan Wang
Department of Physics, College of Science, Inner Mongolia University Technology, Hohhot Inner Mongolia
Received: Feb. 18th, 2019; accepted: Mar. 1st, 2019; published: Mar. 8th, 2019

ABSTRACT
In this paper, we analyzed water viscosity coefficient through exponential fitting and linear fitting in the experiment of measuring by capillary method in engineering colleges. In addition, the higher the timing start height, the closer to the theoretical value.
Keywords:Poiseuille Equation, Viscosity Coefficient, Linear Fit, Exponential Fitting
液体粘滞系数测量实验中的几点思考
贾芸,王景峰,张志浩,高磊,王禹权
内蒙古工业大学理学院物理学系,内蒙古 呼和浩特
收稿日期:2019年2月18日;录用日期:2019年3月1日;发布日期:2019年3月8日

摘 要
本文针对工科院校利用毛细管法测定水的粘滞系数实验分析了指数拟合与线性拟合两种数据处理方案,并对结果进行了比较,另外计时起始高度较高时越接近理论值。
关键词 :泊肃叶公式,粘滞系数,线性拟合,指数拟合

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
粘度是反映液体分子在受到外力作用发生流动时,分子间所呈现的内摩擦力。这种内摩擦力由液体分子的结构、位置、分子间相互作用里及运动状态等参数决定。此外,除了液体本身结构的因素外,温度和压强也是影响液体粘度大小的重要因素。传统的测量方法一般有毛细管法、圆筒旋转法和落球法等 [1] 。由于液体分子结构和分子间相互作用的复杂性,目前还没有一个能够精确计算液体粘度的方法。对粘度的研究主要在实验测量和通过实验数据建立一些经验或半经验公式上,通过实验数据拟合而来 [2] [3] 。本校教材《大学物理实验》 [4] 中,采用南京浪博科教仪器有限公司生产的LB-VC液体粘滞系数测量仪(实验装置示意图见图1所示),进行纯净水的粘滞系数及雷诺数的测定,针对教学中所遇到的问题提出以下几点建议和思考。

Figure 1. Schematic diagram of the experimental device [4]
图1. 实验装置示意图 [4]
2. 逐差法的应用
由泊肃叶公式,液体流量:
(1)
其中a为毛细管的半径,L为毛细管的长度,p为流体两端的净压强(p = pgy),η为液体的粘滞系数,t为时间,V为有效体积。由(1)式得:
(2)
y1,y2分别为液体在不同时刻的高度,由此利用液体密度以及液体从y1到y2下落的时间t通过积分运算得到该液体的粘滞系数η。
(3)
得到:
(4)
其中 是容器的截面积。在公式(3)中令 ,则(4)式可以变换为:
(5)
将(5)式两边取对数得:
(6)
由于y1在实验中是计时起点有效高度,是一个常量,所以由(6)式可看出lny与t为一次函数关系,可以利用逐差法处理数据,经过推导得到:
(7)
我们以计时高度为49.00 cm的实验数据为例(有效高度为 ),计算得到 ,粘滞系数实验值为 。
在(5)式中由于b是小量在计算中可以做一级泰勒展开,则可以改写:
(8)
有(8)式可以看出能够用逐差法近似处理数据:
(9)
其中y0为计时有效高度。以计时高度为49.00 cm的实验数据为例,计算得到粘滞系数实验值为 。
3. 起始测量高度对实验结果的影响
本套实验仪器建议计时高度尽量高一些,我们针对不同计时高度分别进行了实验,实验结果显示测量起始高度从49.00 cm到35.00 cm,利用指数曲线拟合方式计算了相应粘滞系数,结果显示计时高度对粘滞系数的影响并不大。实验用纯水的温度是19.5摄氏度,粘滞系数理论值为1.01745 × 10−3Pa∙s,但由于实验水质的差别,实验手册上给出的理论值并无可参照性。
实验结果显示计时高度为49.00、48.00和47.00厘米时,最接近理论值,并且7组实验毛细管中纯水均是层流状态,满足牛顿流体的假设前提。因此为了实验误差尽可能小计时高度应尽可能高。
Table 1. The relative error of the viscosity coefficient, the average velocity and the corresponding Reynolds number at different timing heights
表1. 不同计时高度下的粘滞系数,与理论粘滞系数相对误差、平均流速和相应雷诺数
4. 曲线拟合与理论计算的比较
在教学中要求学生利用Excel软件对时间和计时有效高度的数据进行指数拟合(如图2所示),后求出(5)式中的b值,继而计算粘滞系数。结果见表1。对比计时高度为49.00 cm时的结果可以看出曲线拟合结果与理论计算的结果完全吻合。
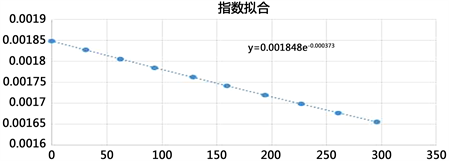
Figure 2. Exponential fitting curve
图2. 指数拟合曲线
综上所述,我们在进行该实验的教学中可以要求计时高度尽可能高,并采用文中多种方案进行数据处理。
基金项目
内蒙古工业大学校重点研究项目ZD201614。
文章引用
贾 芸,王景峰,张志浩,高 磊,王禹权. 液体粘滞系数测量实验中的几点思考
Suggestions on the Measurement of Liquid Viscosity Coefficient[J]. 教育进展, 2019, 09(02): 133-136. https://doi.org/10.12677/AE.2019.92027
参考文献
- 1. 陈慧钊. 粘度测量[M]. 北京: 中国计量出版社, 2003.
- 2. Martins, R.J., Cardoso, M.J.E. de M. and Barcia, O.E. (2003) A New Model Calculating the Viscosity of Pure Liquids at High Pressures. Industrial & Engineering Chemistry Research, 42, 3824-3830. https://doi.org/10.1021/ie021017o
- 3. Shukla, D., Singly, S., Parveen, S., et al. (2007) A Corresponding State Model for the Prediction of the Viscosity of Pure Liquids and Liquid Mixtures. Journal of Molecular Liquids, 136, 111-116. https://doi.org/10.1016/j.molliq.2007.02.005
- 4. 吕军, 王景峰, 等. 大学物理实验[M]. 北京: 高等教育出版社, 2014.
