Pure Mathematics
Vol.07 No.04(2017), Article ID:21402,12
pages
10.12677/PM.2017.74041
Uniqueness of Traveling Wave Solutions for a Quasi-Monotone Reaction-Diffusion Equation with Neutral Type
Yubin Liu
College of Mathematics and Data Science, Huizhou University, Huizhou Guangdong

Received: Jun. 29th, 2017; accepted: Jul. 13th, 2017; published: Jul. 19th, 2017

ABSTRACT
In present paper, we focus on the uniqueness of traveling wave solutions for a quasi-monotone reaction-diffusion equation with neutral type. By using the Ikehara’s Theorem, we firstly establish the asymptotic exponent properties of monotone traveling wave solution with speed 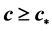 for the reaction-diffusion equation with a infinite number of delays, which is transformed from the neutral equation by a linear variable transform, and then the uniqueness (up to translation) of monotone traveling wave solution with speed
for the reaction-diffusion equation with a infinite number of delays, which is transformed from the neutral equation by a linear variable transform, and then the uniqueness (up to translation) of monotone traveling wave solution with speed  for the transformed equation. Finally, we obtain the uniqueness (up to translation) of monotone traveling wave solution with speed
for the transformed equation. Finally, we obtain the uniqueness (up to translation) of monotone traveling wave solution with speed 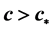 for the neutral equation by using the relation between solutions of the neutral equation and of the transformed equation.
for the neutral equation by using the relation between solutions of the neutral equation and of the transformed equation.
Keywords:Reaction-Diffusion Equation with Neutral Type, Traveling Wave Solution, Quasi-Monotone Reaction, Uniqueness

拟单调中立型反应扩散方程行波解的唯一性
刘玉彬
惠州学院数学与大数据学院,广东 惠州

收稿日期:2017年6月29日;录用日期:2017年7月13日;发布日期:2017年7月19日

摘 要
本文考虑了具有拟单调反应项的中立型反应扩散方程行波解的唯一性问题。首先通过线性变换将方程化为具有无限离散时滞的反应扩散方程,并利用Ikehara定理得到了无限时滞方程波速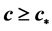 的单调行波解的指数渐近性态,进而得到方程波速
的单调行波解的指数渐近性态,进而得到方程波速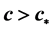 的单调行波解是唯一的(平移意义下),最后根据两类方程的解之间的联系得到了原中立型方程波速
的单调行波解是唯一的(平移意义下),最后根据两类方程的解之间的联系得到了原中立型方程波速 的单调行波解的唯一性(平移意义下)。
的单调行波解的唯一性(平移意义下)。
关键词 :中立型反应扩散方程,行波解,拟单调反应项,唯一性

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文考虑如下中立型反应扩散方程
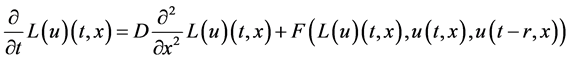 (1.1)
(1.1)
其中 ,
,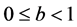 ,
,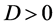 ,
, 是常数。存在常数
是常数。存在常数 使得
使得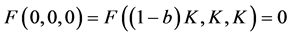 。
。
发展方程的行波解是指形如 (
( ,
,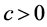 )的形式不变解。此类解不仅揭示了方程本身的许多重要特性,在分析方程初值问题的行为特征中起关键性作用,还具有深刻的应用背景,如物理上描述状态由一个平衡态到另一平衡态的转移、种群生物学中刻画种群入侵、疾病传播动力学中传染源在空间中的传播等等。近二十多年来,研究发展方程,尤其是时滞反应扩散方程的行波解一直是个热点课题,备受众多学者的关注,如行波解的存在性 [1] - [13] 。
)的形式不变解。此类解不仅揭示了方程本身的许多重要特性,在分析方程初值问题的行为特征中起关键性作用,还具有深刻的应用背景,如物理上描述状态由一个平衡态到另一平衡态的转移、种群生物学中刻画种群入侵、疾病传播动力学中传染源在空间中的传播等等。近二十多年来,研究发展方程,尤其是时滞反应扩散方程的行波解一直是个热点课题,备受众多学者的关注,如行波解的存在性 [1] - [13] 。
唯一性是研究行波解理论的又一重要且有趣课题。Diekmann和Kpper发展了一套方法证明了一类积分方程的行波解的唯一性 [14] 。其基本思想是先证明行波解在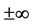 处的指数渐近性态,然后利用此渐近性态证明行波解在平移意义下是唯一的。此思想方法被进一步发展用以讨论非线性积分方程及可化为积分方程的非局部扩散方程 [15] 、一类涵盖多种带离散时滞发展方程 [16] 及具有分布时滞的反应扩散方程 [17] 的行波解的唯一性。其它研究发展方程行波解唯一性的方法及更多关于行波解唯一性的结果参考文献 [18] - [25] 。
处的指数渐近性态,然后利用此渐近性态证明行波解在平移意义下是唯一的。此思想方法被进一步发展用以讨论非线性积分方程及可化为积分方程的非局部扩散方程 [15] 、一类涵盖多种带离散时滞发展方程 [16] 及具有分布时滞的反应扩散方程 [17] 的行波解的唯一性。其它研究发展方程行波解唯一性的方法及更多关于行波解唯一性的结果参考文献 [18] - [25] 。
当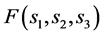 关于
关于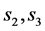 单调时,在适当假设下Liu和Weng利用线性变换、截断及无穷时滞有限逼近等方法得到了方程(1.1)的行波解及渐近播速的存在性,并得出渐近播速与行波解存在的最小波速是一致的结论 [26] 。据我们所知,这是第一个关于中立型反应扩散方程渐近播速和行波解的结果。但中立型反应扩散方程行波解的唯一性至今仍然是个开放性问题。
单调时,在适当假设下Liu和Weng利用线性变换、截断及无穷时滞有限逼近等方法得到了方程(1.1)的行波解及渐近播速的存在性,并得出渐近播速与行波解存在的最小波速是一致的结论 [26] 。据我们所知,这是第一个关于中立型反应扩散方程渐近播速和行波解的结果。但中立型反应扩散方程行波解的唯一性至今仍然是个开放性问题。
本文剩下部分的结构如下:在第2节将给出本文需要的预备知识,包括基本假设及直接应用Liu和Weng [26] 的结果得到的中立型方程(1.1)及其变换后的无穷时滞反应扩散方程的行波解存在结论;第3节先利用Ikehara定理得到了无限时滞方程单调行波解的指数渐近性态,进而得到唯一性;最后根据两类方程的解之间的联系得到了原中立型方程行波解的唯一性。
2. 预备知识
首先我们给出本文需要用到的假设:
(H1) 对任意 ,
,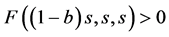 ;对任意
;对任意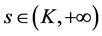 ,
, ;
;
(H2) 对任意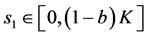 ,
,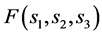 关于
关于 单调增加,且存在
单调增加,且存在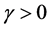 ,使的对任意
,使的对任意 ,
,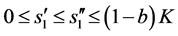 ,有
,有
 ;
;
(H3)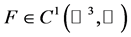 ,
,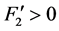 ,
,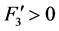 ,
, ,且对任意的
,且对任意的 ,有
,有
 ,
,
其中 ,
,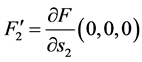 ,
,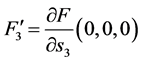 ;
;
(H4) 存在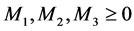 ,使得
,使得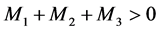 ,且对任意
,且对任意 ,有
,有
 ;
;
(H5) 存在 ,使得对任意的
,使得对任意的 ,
,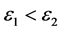 ,存在唯一的
,存在唯一的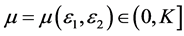 ,使得
,使得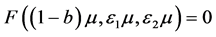 ,且对任意
,且对任意 ,
, ,对任意
,对任意 ,
, ;
;
(H6)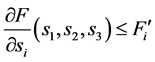 ,
,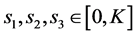 ,
, 。
。
记
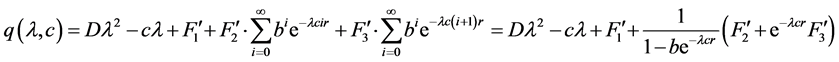
则根据文 [26] 中的Lemma 4.3,有
引理2.1. [26] 假设(H3)成立,则存在实数对 使得:
使得:
(1)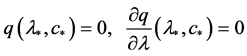 ;
;
(2) 对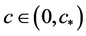 ,当
,当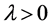 时,有
时,有 ;
;
(3) 对任意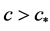 ,存在
,存在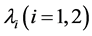 ,使得
,使得 ,
, ,且对任意的
,且对任意的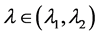 ,
,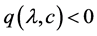 。
。
再由文 [26] 中的Lemma 4.6及Theorem 5.1,有如下关于方程(1.1)的行波解 存在性结果,这里
存在性结果,这里 ,
,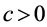 。
。
引理2.2. [26] 假设(H1)~(H5)成立,则
(1) 对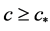 方程(1.1)的行波解
方程(1.1)的行波解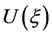 存在,在
存在,在 上单调递增,且满足
上单调递增,且满足
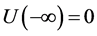 ,
, 
(2) 对 ,方程(1.1)不存在行波解。
,方程(1.1)不存在行波解。
作变换 ,则
,则 且方程(1.1)变为无穷时滞反应扩散方程
且方程(1.1)变为无穷时滞反应扩散方程
 (2.1)
(2.1)
易知(2.1)有平衡点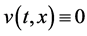 及
及 。
。
由文 [26] 中的Lemma 4.6、Theorem 4.1和Theorem 4.2,方程(2.1)连接平衡点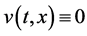 及
及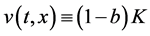 的行波解
的行波解 ,
, 由如下引理给出。
由如下引理给出。
引理2.3. [26] 假设(H1)-(H5)成立,则
(1) 对 方程(2.1)的行波解
方程(2.1)的行波解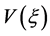 存在,在
存在,在 上单调递增,且满足
上单调递增,且满足
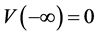 ,
, 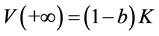
(2) 对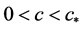 方程(2.1)不存在行波解。
方程(2.1)不存在行波解。
3. 行波解的唯一性
这节我们将证明方程(1.1)的行波解的唯一性,即
定理3.1.假设对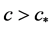 ,
,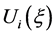 是方程(1.1) 满足
是方程(1.1) 满足
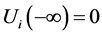 ,
, 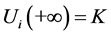
的单调递增行波解, 在
在 上单调递增,(H6)成立且
上单调递增,(H6)成立且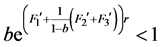 ,则存在
,则存在 ,使得
,使得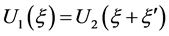 ,
,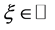 ,其中
,其中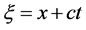 ,
,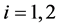 。
。
注:文 [26] 是通过方程(2.1)的单调行波解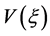 结合变换
结合变换 得到方程(1.1)的单调行波解
得到方程(1.1)的单调行波解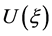 ,这样
,这样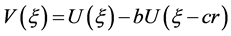 在
在 上单调递增。因此我们这里假设方程(1.1)的单调行波解
上单调递增。因此我们这里假设方程(1.1)的单调行波解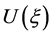 使得
使得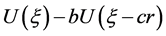 在
在 上单调是合理的。
上单调是合理的。
为了证明定理3.1,需先证明方程(2.1)的单调行波解在平移意义下是唯一的,为此我们需要如下两个引理。
引理3.1.对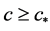 ,设
,设 是方程(2.1)满足
是方程(2.1)满足
 ,
,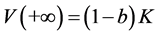
的单调行波解,则存在 ,使得对任意的
,使得对任意的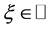 ,有
,有
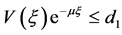 ,
,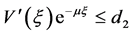 。
。
证明:易知 满足
满足
 (3.1)
(3.1)
重写方程(3.1)为
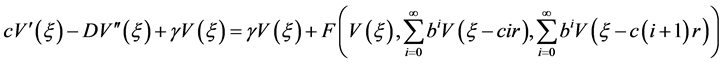
则
 ,
,
其中
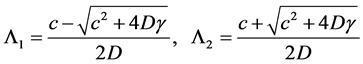 (3.2)
(3.2)
 (3.3)
(3.3)
显然,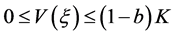 ,
, ,因此
,因此 在
在 上有界,从而
上有界,从而
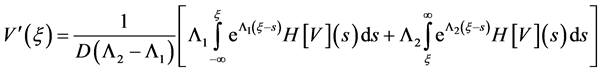
在 上有界,即存在
上有界,即存在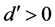 ,使得
,使得 ,
,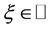 。
。
根据 及
及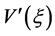 在
在 上的有界性知,对任意的
上的有界性知,对任意的 ,
, 及
及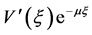 在
在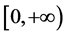 上是有界的。因此往下我们只需证明对某个
上是有界的。因此往下我们只需证明对某个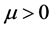 及
及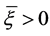 ,
, 及
及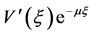 在
在 上有界。
上有界。
由于 ,因此
,因此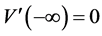 。对任意的
。对任意的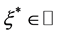 ,对方程(3.1)两边从
,对方程(3.1)两边从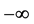 到
到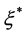 积分得
积分得
 。
。
由(H3),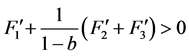 ,
,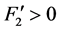 ,
, ,所以存在
,所以存在 ,使得
,使得
 ,
,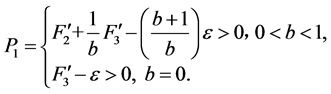
对上述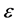 ,存在
,存在 ,使得对任意的
,使得对任意的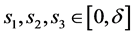 ,有
,有
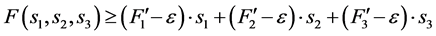 。
。
又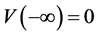 ,所以存在
,所以存在 ,使得对所有的
,使得对所有的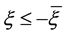 ,有
,有 ,从而对所有的
,从而对所有的 ,有
,有
 (3.4)
(3.4)
对任意的 ,
, ,有
,有

从而由(3.4)可得
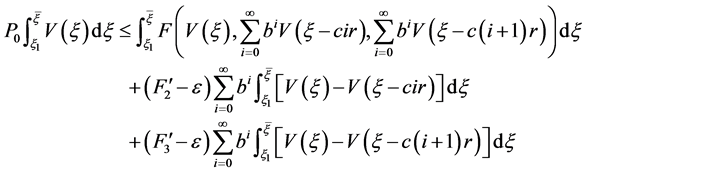
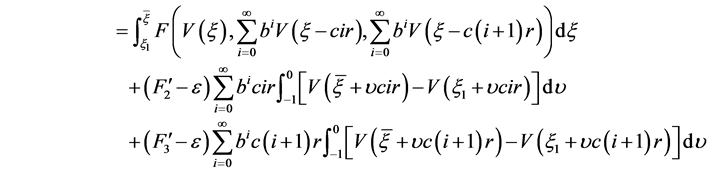 。
。
令 ,由于
,由于 收敛,故有
收敛,故有
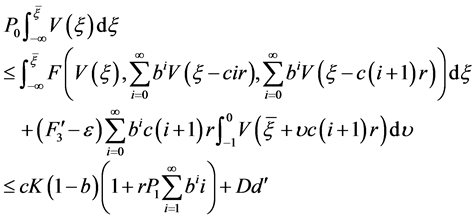 。
。
因此, 在
在 上可积。
上可积。
定义
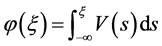 ,
,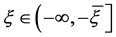 ,
,
则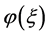 在
在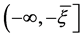 上有定义,单调递增且
上有定义,单调递增且 。
。
根据(3.4),有
 。
。
对任意的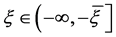 ,对上式两边从
,对上式两边从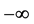 到
到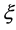 积分得
积分得
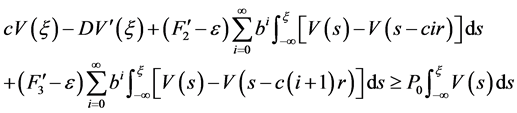 。
。
即
 (3.5)
(3.5)
再对(3.5)式两边从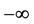 到
到 积分得
积分得
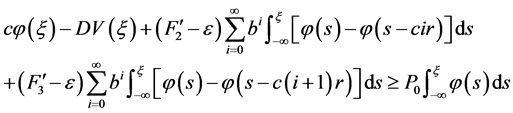
注意到

及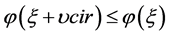 ,
, ,
,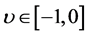 ,
,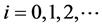 ,有
,有
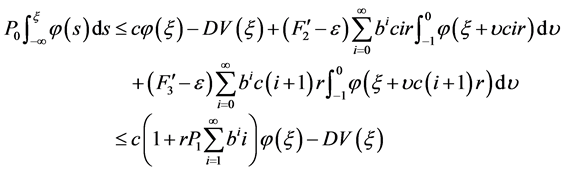 。
。
对任意的 及
及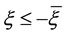 ,有
,有
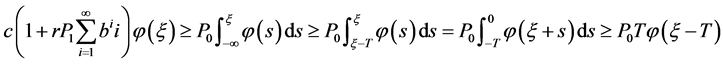 。
。
记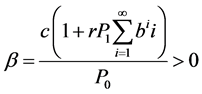 ,取
,取 ;记
;记 ,则
,则 ,
, ;
;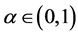 。取
。取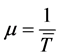 ,则
,则 。定义
。定义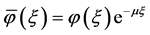 ,
,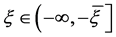 ,则
,则
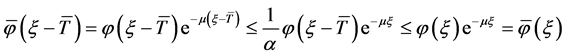 ,
,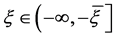 。
。
因此,对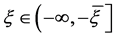 ,有
,有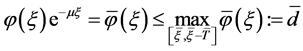 。又
。又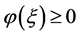 ,
,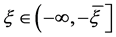 ,故
,故
 ,
, 。
。
根据(3.5),对 ,有
,有
 。
。
至此,证明了存在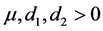 ,使得对任意的
,使得对任意的 ,有
,有
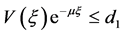 ,
, 。
。
引理3.2.对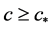 ,设
,设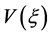 是方程(2.1)的满足
是方程(2.1)的满足
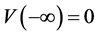 ,
,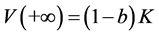
的单调行波解, ,则存在
,则存在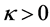 ,使得
,使得
 。
。
其中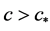 时,
时,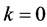 ;
;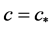 时,
时,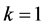 。
。
证明:定义
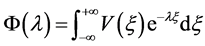 ,
,
由引理3.1知,对任意满足 的复数
的复数 ,
, 。由分部积分法,有
。由分部积分法,有
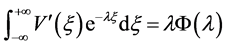 ,
,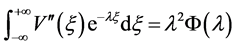 。
。
注意到
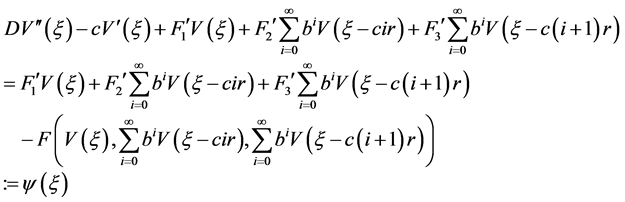 ,
,
故有
 ,
,
即
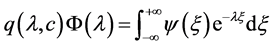 (3.6)
(3.6)
一方面,因为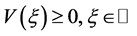 ,由Laplace变换的性质知,存在
,由Laplace变换的性质知,存在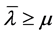 ,
, 在带形域
在带形域 上解析,而点
上解析,而点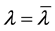 是
是 的奇异点。
的奇异点。
另一方面,由(H4)知,对任意的 ,有
,有
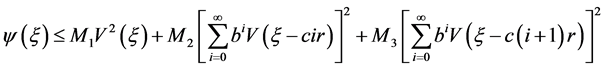 ,
,
又因为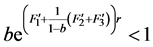 ,所以
,所以
 ,
,
从而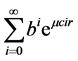 收敛。因此,由引理3.1,有
收敛。因此,由引理3.1,有
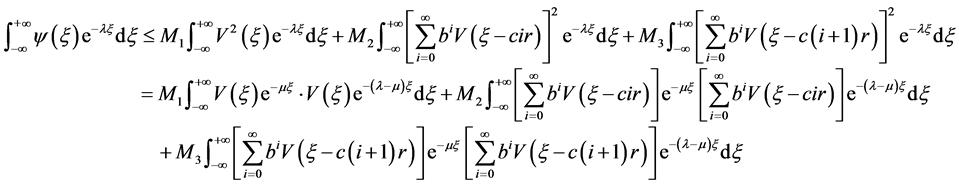

这样 在带形域
在带形域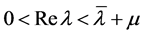 上解析。类似于文 [17] 中Proposition 2.3 的证明,可得
上解析。类似于文 [17] 中Proposition 2.3 的证明,可得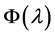 在带形域
在带形域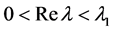 上解析,而
上解析,而 在带形域
在带形域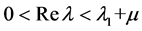 上解析。
上解析。
定义函数
 .
.
因为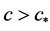 时
时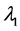 是方程
是方程 单根,
单根, 时
时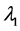 是方程
是方程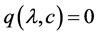 二重根,所以由(3.6)有
二重根,所以由(3.6)有
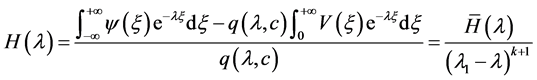 ,
,
其中
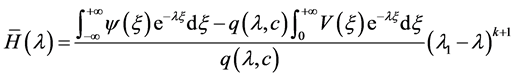
在带形域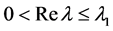 上解析,
上解析,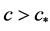 时,
时, ;
; 时,
时,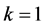 。
。
又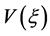 在
在 单调递增,因此由Ikehara定理有
单调递增,因此由Ikehara定理有
 ,
,
其中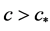 时,
时,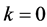 ;
; 时,
时,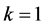 。证毕。
。证毕。
引理3.3.假设(H6)成立。若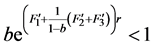 ,则对任意的
,则对任意的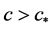 ,方程(2.1) 满足
,方程(2.1) 满足
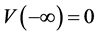 ,
,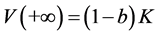
的单调行波解在平移意义下是唯一的。
证明:对任意的 ,设
,设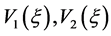 是方程(2.1) 满足
是方程(2.1) 满足
 ,
,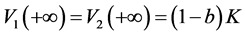
的两个单调行波解。不失一般性,不妨设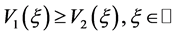 ,由引理3.2,可定义函数
,由引理3.2,可定义函数
 ,
,
使得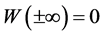 (必要时作适当的平移),从而存在
(必要时作适当的平移),从而存在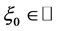 ,使得
,使得
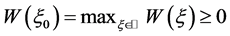 。
。
由于 ,
, ,且
,且
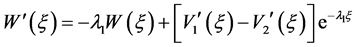 ,
,
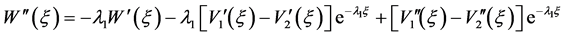 ,
,
因此,
 ,
,
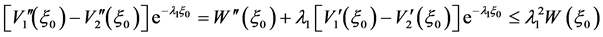 。
。
由(H6),有
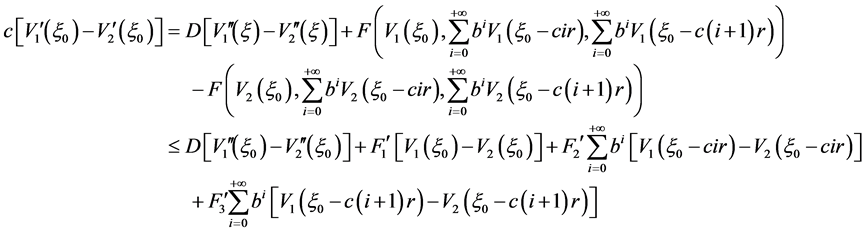
进一步地,有
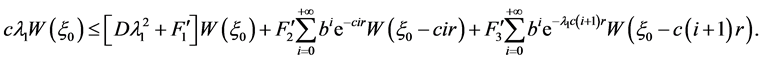
注意到 ,因此有
,因此有
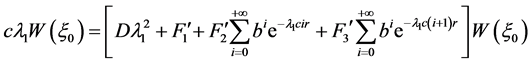 ,
,
从而可得
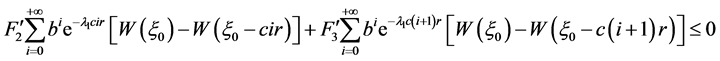 ,
,
这意味着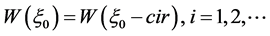 。令
。令 ,则
,则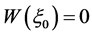 ,即
,即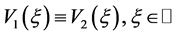 。证毕。
。证毕。
定理3.1的证明:设存在某个 ,使得对任意的
,使得对任意的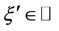 ,
,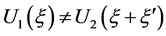 。令
。令
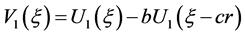 ,
,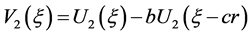 ,
,
则 是方程(2.1)满足
是方程(2.1)满足
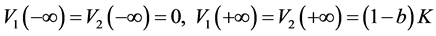 ,
,
的单调行波解。由引理3.3知,存在 ,使得
,使得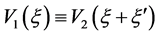 ,从而
,从而
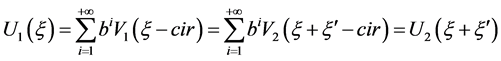 。
。
这与假设矛盾,因此定理3.1的结论成立。证毕。
基金项目
感谢审稿人的认真审稿及提出的珍贵意见。本文受如下基金项目资助: 国家自然科学基金(No.11601180, 11501238),国家留学基金(No.201608440052),广东省自然科学基金 (No.2016A030310100, 2015A030313574, 2014A030313641),广东省教育厅青年人才创新项目(No.2015KQNCX155)。
文章引用
刘玉彬. 拟单调中立型反应扩散方程行波解的唯一性
Uniqueness of Traveling Wave Solutions for a Quasi-Monotone Reaction-Diffusion Equation with Neutral Type[J]. 理论数学, 2017, 07(04): 310-321. http://dx.doi.org/10.12677/PM.2017.74041
参考文献 (References)
- 1. Schaaf, K.W. (1987) Asymptotic Behavior and Traveling Wave Solutions for Parabolic Functional Differential Equations. Transactions of the American Mathematical Society, 302, 587-615.
- 2. Chow, S.N., Paret, M.J. and Shen, W.X. (1998) Travelling Waves in Lattice Dynamical Systems. Journal of Differential Equations, 149, 248-291.
- 3. Ma, S.W. (2001) Traveling Wavefronts for Delayed Reaction-Diffusion Systems via a Fixed Point Theorem. Journal of Differential Equations, 171, 294-314.
- 4. Al-Omari, J. and Gourley, S.A. (2002) Monotone Traveling Fronts in Age-Structured Reaction Diffusion Model of a Single Species. Journal of Mathematical Biology, 45, 294-312. https://doi.org/10.1007/s002850200159
- 5. Al-Omari, J. and Gourley, S.A. (2005) Monotone Wavefront in a Structured Population Model with Distributed Maturation Delay. IMA Journal of Applied Mathematics, 70, 858-879. https://doi.org/10.1093/imamat/hxh073
- 6. 黄建华, 黄立宏. 高维格上时滞反应扩散方程的行波解[J]. 应用数学学报, 2005(1): 100-113.
- 7. Liang, X. and Zhao, X.Q., (2007) Asymptotic Spreading Speeds of Spread and Traveling Waves for Monotone Semiflows with Application. Communications on Pure Applied Mathematics, 60, 1-40. Erratum: (2008) 61, 137-138.
- 8. Wang, H.Y. (2009) On the Existence of Traveling Waves for Delayed Reaction-Diffusion Equations. Journal of Differential Equations, 247, 887-905.
- 9. 梁飞, 高洪俊. 非局部时滞反应扩散方程行波解的存在性[J]. 数学物理学报, 2011(5): 1273-1281.
- 10. Fang, J. and Zhao, X.Q. (2014) Traveling Waves for Monotone Semiflows with Weak Compactness. SIAM Journal on Mathematical Analysis, 46, 3678-3704.
- 11. 黄业辉, 翁佩萱. 一个具有非局部效应的非线性周期反应扩散方程的渐近形态[J]. 数学学报, 2014(5): 1011- 1030.
- 12. 尚德生, 张耀明. 具有分布时滞的一类反应扩散方程的波前解的存在性[J]. 生物数学学报, 2015(3): 415-424.
- 13. 边乾坤, 张卫国, 余志先. 具有时滞的时间离散反应扩散系统行波解的存在性[J]. 应用数学, 2016(2): 359-369.
- 14. Diekmann, O. and Kapper, H.G. (1978) On the Bounded Solutions of a Nonlinear Convolution Equation, Nonlinear Analysis. Theory, Methods and Applications, 2, 721-737.
- 15. Fang, J. and Zhao, X.Q. (2010) Existence and Uniqueness of Traveling Waves for Non-Monotone Integral Equations with Applications. Journal of Differential Equations, 248, 2199-2226.
- 16. Aguerrea, M., Gomez, C. and Trofimchuk, S. (2012) On Uniqueness of Semi-Wave Fronts: Diekmann-Kapper Theory of a Nonlinear Convolution Equation Re-Visited. Mathemtische Annalen, 354, 73-109. https://doi.org/10.1007/s00208-011-0722-8
- 17. Xu, Z.Q. and Xiao, D.M. (2016) Spreading Speeds and Uniqueness of Traveling Waves for a Reaction Diffusion Equation with Spatio-Temporal Delays. Journal of Differential Equations, 260, 268-303.
- 18. Chen, X.F. and Guo, J.S. (2003) Uniqueness and Existence of Traveling Waves for Discrete Quasilinear Monostable Dynamics. Mathematische Annalen, 326, 123-146. https://doi.org/10.1007/s00208-003-0414-0
- 19. Carr, J. and Chmaj, A. (2004) Uniqueness of Traveling Waves for Nonlocal Monostable Equations. Proceedings of American Mathematical Society, 132, 2433-2439. https://doi.org/10.1090/S0002-9939-04-07432-5
- 20. Ma, S.W. and Zou, X.F. (2005) Existence, Uniqueness and Stability of Travelling Waves in a Discrete Reaction-Diffusion Monostable Equation with Delay. Journal of Differential Equations, 217, 54-87.
- 21. Aguerrea, M., Trofimchuk, S. and Valenzuela, G. (2008) Uniqueness of Fast Travelling Fronts in Reaction-Diffusion Equations with Delay. Proceedings of the Royal Society A, 464, 2591-2608. https://doi.org/10.1098/rspa.2008.0011
- 22. Guo, J.S. and Wu, C.H. (2008) Existence and Uniqueness of Traveling Waves for a Monostable 2-D Lattice Dynamical System. Osaka Journal of Mathematics, 45, 327-346.
- 23. Wu, S.L. and Liu, S.Y. (2009) Uniqueness of Non-Monotone Traveling Waves for Delayed Reaction-Diffusion Equations. Applied Mathematics Letters, 22, 1056-1061.
- 24. Zhao, H.Q., Weng, P.X. and Liu, S.Y. (2014) Uniqueness and Stability of Traveling Wave Fronts for an Age-Structured Population Model in a 2D Lattice Strip. Communications in Nonlinear Science and Numerical Simulation, 19, 507-519.
- 25. Yang, Y.R. and Liu, N.W. (2014) Monotonicity and Uniqueness of Traveling Waves in Bistable Systems with Delay. Electronic Journal of Differential Equations, No. 2, 1-12.
- 26. Liu, Y.B. and Weng, P.X. (2015) Asymptotic Pattern for a Partial Neutral Functional Differential Equation. Journal of Differential Equations, 258, 3688-3741.