Pure Mathematics
Vol.
10
No.
05
(
2020
), Article ID:
35660
,
6
pages
10.12677/PM.2020.105063
Zero-Zero-Hopf Bifurcation of a Hyperchaotic Faraday Disk Dynamo
Huanyu Yu
School of Mathematics, South China University of Technology, Guangzhou Guangdong

Received: Apr. 21st, 2020; accepted: May 12th, 2020; published: May 20th, 2020

ABSTRACT
The paper investigates the bifurcation of periodic solutions at the zero-zero-Hopf equilibrium of a hyperchaotic Faraday disk dynamo. By means of the averaging theory, the paper obtains the sufficient conditions that two periodic solutions will appear at the bifurcation point and discusses the stability of the two orbits.
Keywords:Faraday Disk Dynamo, Hyperchaos, Zero-Zero-Hopf Bifurcation, Periodic Solution, Averaging Theory

一类超混沌的Faraday圆盘发电机的Zero-Zero-Hopf分支
余环宇
华南理工大学数学学院,广东 广州
收稿日期:2020年4月21日;录用日期:2020年5月12日;发布日期:2020年5月20日

摘 要
本文主要研究了一类四维的self-exciting Faraday圆盘发电机,它描述了azimuthal eddy流的作用。首先通过计算Lyapunov指数,发现该系统是一个超混沌的系统。然后研究了系统的zero-zero-Hopf分支。利用平均理论,获得了在zero-zero-Hopf分支点存在两个周期解的充分条件,并进一步讨论了周期解的稳定性。
关键词 :Faraday圆盘发电机,超混沌,Zero-Zero-Hopf分支,周期解,平均理论

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1996年,Hide等提出了一个self-exciting Faraday圆盘单极发电机,它是一个非线性的三维动力系统 [1]。在此基础上,逐渐发展了很多改进的模型 [2] - [10],其中Hide和Moroz提出了一类四维的发电机,它描述了方位涡流(azimuthal eddy currents)的作用。其模型如下:
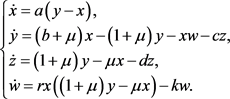 (1.1)
(1.1)
其中x和y分别表示圆盘和线圈的磁通量,z表示电动机电枢的角转速,w表示圆盘的角转速。
Moroz在文献 [11] 中已经做了一些数值分析去研究系统(1.1)的zero-zero-Hopf分支,然而并没有严格的证明。本文将给出系统存在zero-zero-Hopf分支的证明,并把相应的周期解求出来。
一个zero-Hopf或zero-zero-Hopf奇点意味着可能出现混沌。近年来,虽有一些文献研究三维混沌系统的zero-Hopf分支 [12] [13] [14],但由于高维系统的复杂性,对四维及以上系统的zero-zero-Hopf分支的研究非常少 [15]。Cid-Montiel等在文献 [15] 中研究了一个四维超混沌的Lorenz系统的zero-Hopf分支。Chen 等在文献 [16] 中研究了一个广义Lorenz-Stenflo超混沌系统zero-zero-Hopf分支。
2. 超混沌和zero-zero-Hopf分支
系统(1.1) 总有一个奇点 。当 时,还有如下的两个奇点:
,
其中 。
对初始值 和参数 ,我们计算出来Lyapunov指数是0.2927,0.1826,0,−19.0777。因此系统是超混沌的,图1显示了一个超混沌吸引因子。
图1是系统(1.1)的超混沌吸引因子,其中初始值 ,参数 。
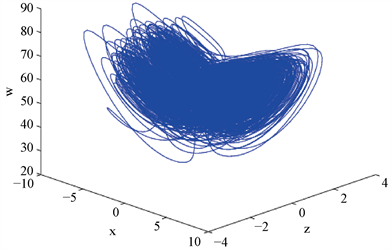
Figure 1. Hyperchaotic attraction factor of system (1.1)
图1. 系统(1.1)的超混沌吸引因子
下面我们应用平均理论去研究系统(1.1)的zero-zero-Hopf分支。当 ,一些表达式过于庞大。为了表达的方便,我们令 。
理论1 对 ,原点 是系统(1.1)的一个zero-zero-Hopf奇点。在 的特征值是0,0, ,其中 。
证明. 在 的特征方程是
(2.1)
当 时,(2.1)有根0,0, ,其中 。
利用平均理论,我们能证明下面的定理。
理论2 令
这里 。
假设 ,那么系统(1.1)有一个zero-zero-Hopf分支。当 且 足够小时,在 产生两个周期解。如果 ,那么这两个周期解是稳定的。
证明. 作变换
系统(1.1)变成
(2.2)
令 。我们把 又表示为 ,那么系统(2.2)变为
(2.3)
下面利用平均理论来研究系统(2.2)的动力学行为。首先我们考虑下面这个未扰动系统的初值问题
(2.4)
系统(2.4)的解是 ,其中
当 时,系统(2.4)的所有解 是周期的,其中周期为 。沿着一个周期解 ,
其线性化系统 的基解矩阵 是
其中
计算积分
其中
解方程 ,我们得到下面的解
对应奇点 。对其他两个解 和 ,我们有
因此根据平均理论,系统(2.3)存在的两个周期为T的解
和
,当 时,有
和
。考虑到系统(2.2)和(2.3)的关系,系统(2.3)的两个周期解分别对应系统(2.2)的两个周期解
和
。
时,有
和
。考虑到系统(2.2)和(2.3)的关系,系统(2.3)的两个周期解分别对应系统(2.2)的两个周期解
和
。
最后,我们计算Jacobian矩阵 和 的特征值来判断两个周期解的稳定性。对这两个矩阵而言,特征多项式是相同的,如下
(2.5)
当 时,方程(2.5)的根都有负实部,这意味着在 产生的两个周期解 和 是稳定的。
3. 结束语
通过选取适当的参数,我们计算发现系统有两个正的Lyapunov指数,是一个超混沌的系统。不同于前人的数值工作,本文对系统存在zero-zero-Hopf分支给出了严格的证明,并给出了周期解的表达式,以及周期解稳定的条件。
文章引用
余环宇. 一类超混沌的Faraday圆盘发电机的Zero-Zero-Hopf分支
Zero-Zero-Hopf Bifurcation of a Hyperchaotic Faraday Disk Dynamo[J]. 理论数学, 2020, 10(05): 518-523. https://doi.org/10.12677/PM.2020.105063
参考文献
- 1. Hide, R., Skeldon, A.C. and Acheson, D.J. (1996) A Study of Two Novel Self-Exciting Single-Disk Homopolar Dy-namos: Theory. Proceedings of the Royal Society of London. Series A, 452, 1369-1395. https://doi.org/10.1098/rspa.1996.0070
- 2. Hide, R. (1997) Nonlinear Quenching of Current Fluctuations in a Self-Exciting Homopolar Dynamo. Nonlinear Processes in Geophysics, 4, 201-205. https://doi.org/10.5194/npg-4-201-1997
- 3. Hide, R. (1997) The Nonlinear Differential Equations Governing a Hierarchy of Self-Exciting Coupled Faraday-Disk Homopolar Dynamos. Physics of the Earth and Planetary Interiors, 103, 281-291. https://doi.org/10.1016/S0031-9201(97)00038-1
- 4. Hide, R. (2000) Generic Nonlinear Processes in Self-Exciting Dynamos and the Long-Term Behaviour of the Main Geomagnetic Field, Including Polarity Superchrons. Philosophical Transactions of the Royal Society A, 358, 943-955. https://doi.org/10.1098/rsta.2000.0568
- 5. Moroz, I.M., Hide, R. and Soward, A.M. (1998) On Self-Exciting Coupled Faraday Disk Homopolar Dynamos Driving Series Motors. Physica D, 117, 128-144. https://doi.org/10.1016/S0167-2789(97)00305-9
- 6. Moroz, I.M. (2001) On the Behavior of a Self-Exciting Faraday Disk Homopolar Dynamo with Battery in the Presence of an External Magnetic Field. International Journal of Bifurcation and Chaos, 11, 1695-1705. https://doi.org/10.1142/S0218127401002948
- 7. Moroz, I.M. (2001) Self-Exciting Faraday Disk Homopolar Dynamos. International Journal of Bifurcation and Chaos, 11, 2961-2975. https://doi.org/10.1142/S0218127401004017
- 8. Moroz, I.M. (2002) On the Behavior of a Self-Exciting Faraday Disk Homopolar Dynamo with a Variable Nonlinear Series Motor. International Journal of Bifurcation and Chaos, 12, 2123-2135. https://doi.org/10.1142/S0218127402005728
- 9. Moroz, I.M. (2005) The Extended Malkus-Robbins Dynamo as a Perturbed Lorenz System. Nonlinear Dynamics, 41, 191-210. https://doi.org/10.1007/s11071-005-2808-x
- 10. Hide, R. and Moroz, I.M. (1999) Effects Due to Induced Azi-muthal Eddy Currents in a Self-Exciting Faraday Disk Homopolar Dynamo with a Nonlinear Series Motor. I.: Two Special Cases. Physica D, 134, 287-301. https://doi.org/10.1016/S0167-2789(99)00107-4
- 11. Moroz, I.M. (2011) Unstable Periodic Orbits in a Four-Dimensional Faraday Disk Dynamo. Geophysical & Astrophysical Fluid Dynamics, 105, 273-286. https://doi.org/10.1080/03091929.2010.511206
- 12. Llibre, J. and Makhlouf, A. (2016) Zero-Hopf Bifurcation in the Generalized Michelson System. Chaos Solitons & Fractals, 89, 228-231. https://doi.org/10.1016/j.chaos.2015.11.013
- 13. Euzebio, R.D. and Llibre, J. (2017) Zero-Hopf Bifurcation in a Chua System. Nonlinear Analysis: Real World Applications, 37, 31-40. https://doi.org/10.1016/j.nonrwa.2017.02.002
- 14. Candido, M.R. and Llibre, J. (2018) Zero-Hopf Bifurcations in 3-Dimensional Differential Systems with No Equilibria. Mathematics and Computers in Simulation, 151, 54-76. https://doi.org/10.1016/j.matcom.2018.03.008
- 15. Cid-Montiel, L., Llibre, J. and Stoica, C. (2014) Zero-Hopf Bifurcation in a Hyperchaotic Lorenz System. Nonlinear Dynamics, 75, 561-566. https://doi.org/10.1007/s11071-013-1085-3
- 16. Chen, Y.M. and Liang, H.H. (2017) Zero-Zero-Hopf Bifurcation and Ultimate Bound Estimation of a Generalized Lorenz-Stenflo Hyperchaotic System. Mathematical Methods in the Applied Sciences, 40, 3424-3432. https://doi.org/10.1002/mma.4236
NOTES
*通讯作者。