Mechanical Engineering and Technology
Vol.
09
No.
02
(
2020
), Article ID:
35314
,
8
pages
10.12677/MET.2020.92017
Inverse-Solution Algorithm of Robot Based on Screw Theory and Paden-Kahan Sub-Problem
Yuan Meng1, Shipeng Hao1, Baojun Shi1,2*
1School of Mechanical and Electrical Engineering, Shandong Jianzhu University, Ji’nan Shandong
2School of Mechanical Engineering, Hebei University of Technology, Tianjin

Received: Apr. 13th, 2020; accepted: Apr. 17th, 2020; published: Apr. 28th, 2020

ABSTRACT
The kinematics analysis of industrial robots includes forward kinematics analysis and reverse kinematics analysis. The problem of inverse kinematics solution is a hot and difficult point. Based on the screw theory and geometry method, and combined with Paden-Kahan sub-problem solution, this paper presents a kinematic inverse solution algorithm for robots. Taking a six-axis series industrial robot as an example, given a set of joint angles, the kinematic positive solution is solved. And then several sets of kinematic inverse solutions are obtained as theoretical values. Then, the above inverse solution algorithm based on the screw theory is used to verify its effectiveness. The typical application results show that the inverse kinematics solution algorithm can avoid the singularity problem caused by the parallel joint axis in the D-H parameter method, which not only meets the requirement of repeated positioning accuracy of industrial robot, but also can make the robot move more stable.
Keywords:Screw Theory, Paden-Kahan Sub-Problem, Kinematic Inverse Solution, Industrial Robot

基于旋量理论和Paden-Kahan子问题的 机器人反解算法
孟原1,郝世鹏1,史宝军1,2*
1山东建筑大学机电工程学院,山东 济南
2河北工业大学机械工程学院,天津
收稿日期:2020年4月13日;录用日期:2020年4月17日;发布日期:2020年4月28日

摘 要
对工业机器人进行运动学分析包括正向运动学分析和反向运动学分析,运动学反解问题是当前研究的热点和难点。本文以旋量理论和几何法为基础,结合Paden-Kahan子问题解法,给出一种机器人运动学反解算法。以某六轴串联工业机器人为例,给定一组关节角度,求解出其运动学正解,以此为基础得到若干组运动学反解作为理论值,然后利用上述基于旋量理论的反解算法验证其有效性。典型应用结果表明:该机器人运动学反解算法,可避免D-H参数法中因为关节轴平行引起的奇异性问题,不仅满足对工业机器人重复定位精度的要求,并能够使机器人运动更加平稳。
关键词 :旋量理论,Paden-Kahan子问题,运动学反解,工业机器人

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
工业机器人的运动学求解通常包括正解和反解两个过程。正解是通过给定机器人各个关节的转动角度,然后通过运动学方程求解出工业机器人末端部件的坐标位置以及机器人的姿态;而反解是根据机器人末端部件在空间中的位置和姿态,反向求解出此位置和姿态下各个关节需要运动的角度。反解问题也是当前工业机器人运动学分析的重点和难点。以串联工业机器人为例,其常见的反解的求解方法有:数值法、解析法、几何法等 [1] [2] [3] [4]。数值法又有直接法和间接法之分,需要在进行数值迭代的基础上进行求解,其中直接法需要在机器人运动学方程为显式方程时才能使用,而间接法因为计算量较大且有一定误差,故计算效率和准确度有所下降;几何法需要根据具体问题具体分析,但其计算效率和精度较高;解析法需要满足机器人后3个关节的轴线相交于一点或有3个关节轴相互平行时才能使用,优点是计算效率较高,也相对直观、简单一些。
进行工业机器人运动学分析,不论采用何种分析方法,都需要先建立机器人的运动学模型,目前主要运用的建模方法有:D-H参数法 [3] 和旋量理论法 [4] [5] [6] [7]。D-H参数法优点:通用性强,对机器人的类型、结构和复杂程度没有限制,但建模步骤较为复杂,需要在每个关节轴上建立相对坐标系,然后通过坐标转换逐步实现运动学模型的建立。旋量理论法的优点:根据机器人各个关节轴线的位置和姿态,描述末端部件的位置和姿态,然后将基于旋量理论的反解问题和指数积分相结合,从而将机器人的运动转化为转动和平动的组合,这样便可以在绝对坐标系中更直观地描述机器人的运动情况。
本文基于旋量理论法建立机器人运动学模型,主要是以各个关节运动副的旋转轴或运动方向轴线为基础来完成模型构建,结合Paden-Kahan子问题解法,给出一种机器人运动学反解算法。文中以某型号的串联工业机器人为例,验证了所构建模型与反解算法的有效性。
2. 旋量理论与机器人运动学反解
2.1. 旋量理论
Chasles定理 [8] 证明:任意刚体都可以用一段绕某直线的转动和沿该直线的移动的复合叠加,代替原有的从一个位形到另一个位形的运动。这种将转动和移动复合在一起代替原来运动的方法,称之为螺旋运动。而螺旋运动的无穷小量就是李代数元素,即运动旋量,这样就将李群、旋量和螺旋运动有机地结合起来了。如图1所示的螺旋运动示意图。

Figure 1. Spiral motion
图1. 螺旋运动
在考虑刚体在空间中位姿的表示时,设S表示绝对坐标系,T为固定于刚体上的相对坐标系。则刚体在S上的位姿可以通过T对S的相对位姿来描述,这种变换矩阵的集合表示为:
(1)
式中, 为三维空间中刚体变换的特殊欧式群,即李群;t为相对坐标系相对绝对坐标系的位置,R为相对坐标系相对绝对坐标系的姿态。用 表示李群 的李代数, 为刚体绕定轴旋转时旋转方向的单位矢量,旋转的角度为 , 为旋转轴上的一定点。其中的元素定义如下:
(2)
(3)
式中,v是3行的列矢量, , 为3阶的反对称矩阵。
称为运动旋量,是一个4阶的矩阵。 为运动旋量 的旋量坐标,是一个6行的列向量。
由旋量理论可知,刚体的螺旋运动,可以采用运动旋量的指数坐标来表示,即任何刚体运动 ,都有 。
(4)
式中, 。
这样,可以得到在刚体上的相对坐标系相对于绝对坐标系的位姿变换用刚体运动 的表示,以 表示相对坐标系相对于绝对坐标系的初始位姿,那么刚体相对于某一特定轴做螺旋运动,就可以表示为:
(5)
2.2. 机器人运动学正向运动的旋量表示
以某型号六关节串联机器人为例,其结构简图如图2所示。该型机器人共有6个关节,在前3个关节中,关节2、3的轴线平行,并与关节1的轴线异面垂直;其后3个关节轴线相交于一点。
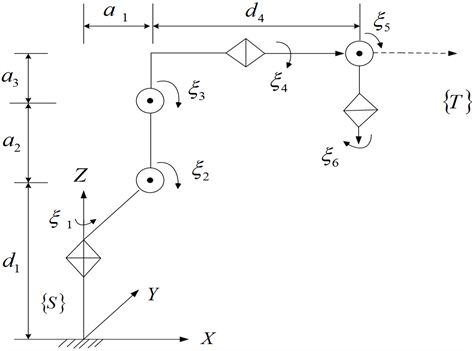
Figure 2. Schematic diagram of a series industrial robot structure
图2. 某串联工业机器人结构简图
以 和 分别计算相对应各连杆的运动旋量 、运动旋量坐标 和相对应旋转运动的指数积分 ,然后根据刚体运动的指数形式,利用指数积分形式表示该机器人基于旋量理论的运动学正解为:
(6)
2.3. 基于旋量理论的运动学反解
在进行机器人运动学反解求解时,若是纯转动问题,需要遵守三个原则:位置不变原则、距离不变原则、姿态不变原则 [9]。前两个原则与转动运动有关,第三个原则与移动运动有关。本文基于旋量理论和几何法,并结合Paden-Kahan [10] 子问题解法,求解机器人运动学反解。
以图2所示某型号六轴工业机器人为例,对其进行运动学反解的求解,即在某一位置和姿态下,求解其6个关节轴的角度。
首先求出前3个关节的角度,然后定义后3个关节轴的交点为,根据旋量理论有:
(7)
将公式(7)代入公式(6)进行解耦,等号两边同右乘 得:
(8)
式中: ,。
通过解耦,将机器人运动学反解问题,转化为前3个关节角和后3个关节角的求解问题,其中前3个关节的运动为从点 出发,经过旋转运动到达终点 ,如图3所示。
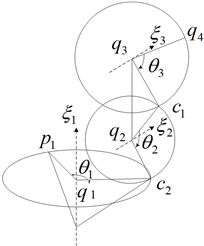
Figure 3. The spiral motion of the first three joints
图3. 前3个关节的螺旋运动图
具体推导过程省略,这里直接给出前3个关节角的计算公式如下:
(9)
(10)
(11)
然后,基于Paden-Kahan子问题解法,具体推导过程省略,直接给出求解后3个关节角度的计算公式如下:
(12)
(13)
(14)
3. 应用实例
首先,将上述机器人运动反解算法应用于机器人末端位置参数的求解。图2所示六轴工业机器人,做正向运动时的关节角度如表1所示。
Table 1. Industrial robot each joint angle
表1. 工业机器人各个关节角度
将上述的关节角度代入机器人正向运动学方程,得到其末端部件的位置参数如表2所示。其中,n、o、a矩阵分别为相对坐标系的x、y、z轴对于参考坐标系的方向余弦;p为相对坐标系对于参考坐标系的位置向量。
Table 2. Position parameter of end part
表2. 末端部件的位置参数
利用表2中得到的末端位置参数,结合本文给出的基于旋量理论和Paden-Kahan子问题得到的反解公式,可得到6个关节的反解。通过多次运算并排除奇异性解,得到8组反解,对应的各个关节的角度汇总如表3所示。
观察表3中的各个关节轴的角度可以发现,第一组数据与表1中给定的初始数据较为接近,因此选择表3中的第一组数据代入正向运动学方程中,最后得到的末端部件位置参数如表4所示。
将表2与表4中的位置参数数据进行对比,可以得到基于旋量理论的反解结果与理论值之间的误差值,如表5所示。
Table 3. The angle of each joint obtained by solving the inverse kinematics solution
表3. 运动学反解求解得到的各个关节角度
Table 4. The position parameters of the terminal components obtained from the first group of inverse solutions
表4. 由第1组反解结果求得的末端部件位置参数
Table 5. System resulting data of standard experiment
表5. 位置参数误差
由表5中的误差数据可以看到,这里的位置参数误差的数量级均在10−5以下,而对于大型工业机器人重复定位精度的要求一般在0.2 mm左右,例如根据KUKA机器人的使用说明书,它规定机器人重复定位精度为0.15 mm [11]。所以,通过旋量理论求解的机器人运动反解,能够满足其重复定位精度的要求。
其次,将上述机器人运动反解算法应用于机器人运动平稳性分析。机器人的运动平稳性,即机器人在运动过程中的速度/加速度变化是否平稳,我们选择加速度为评价指标,采用基于旋量理论的反解算法,求解机器人加速度变化情况,并与D-H算法得到的反解结果进行比较。图4给出了两种反解算法求得的第4关节的最大加速度变化情况,图5给出了两种反解算法求得的第4关节的最小加速度变化情况。从图4和图5中可以明显地看出,利用旋量理论法求得的关节加速度相较于D-H参数法更加平稳。
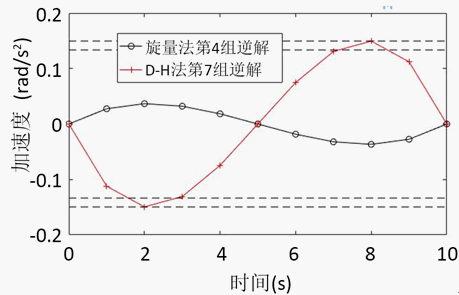
Figure 4. Comparison of the maximum acceleration corresponding to the two inverse solutions at joint 4
图4. 第4关节处两种反解方法对应的最大加速度对比

Figure 5. The comparison of the minimum acceleration between the two anti solutions at joint 4
图5. 第4关节处两种反解方法对应的最小加速对比
4. 结论
本文基于旋量理论和几何法,建立机器人运动学模型,结合Paden-Kahan子问题,构建了一种用于机器人运动学反解的算法。以某六轴串联工业机器人为例,从机器人运动精度和运动稳定性方面,检验了该算法的有效性,并与D-H参数法进行了比较。
典型应用结果表明:本文给出的基于旋量理论和Paden-Kahan子问题的机器人运动学反解算法,避免了D-H参数法中因为关节轴平行造成的奇异性问题,不仅满足工业机器人重复定位精度的要求,而且可获得更好的运动平稳性。
上述机器人运动反解方法对其它工业机器人的适用性,有待后续开展更深入的研究。
基金项目
国家重点研发计划(2017YFB1301300);河北省自然科学基金(E2019202338)。
文章引用
孟 原,郝世鹏,史宝军. 基于旋量理论和Paden-Kahan子问题的机器人反解算法
Inverse-Solution Algorithm of Robot Based on Screw Theory and Paden-Kahan Sub-Problem[J]. 机械工程与技术, 2020, 09(02): 163-170. https://doi.org/10.12677/MET.2020.92017
参考文献
- 1. Paul, R.P. and Shimano, B. (1978) Kinematic Control Equations for Simple Manipulators. 1978 IEEE Conference on Decision and Control Including the 17th Symposium on Adaptive Processes, San Diego, 1398-1406. https://doi.org/10.1109/CDC.1978.268148
- 2. Manocha, D. and Canny, J.F. (1994) Efficient Inverse Kinematics for General 6R Manipulators. IEEE Transactions on Robotics and Automation, 10, 648-657. https://doi.org/10.1109/70.326569
- 3. Denavit, J. and Hartenberg, R.S. (1995) A Kinematic Notation for Lower Pair Mechanisms Based on Matrices. Journal of Applied Mechanics, 2l, 215-221.
- 4. 屈淑维, 李瑞琴, 郭志宏. 基于旋量理论3-RRR平面并联机构的误差分析[J]. 机械设计与研究, 2019, 35(2): 60-62+68.
- 5. 温贻芳, 王太勇, 徐朋. 等离子冗余机器人逆运动学分析与试验[J]. 机械设计与研究, 2019, 35(1): 31-34.
- 6. 裴九芳, 许德章, 王海. 基于旋量理论的三指机器人灵巧手逆运动学分析[J]. 中国机械工程, 2017, 28(24): 2975-2980.
- 7. 吴海淼, 陈鹏, 崔国华, 崔康康, 刘健. 基于改进四阶矩估计法的六轴机器人运动可靠性分析[J]. 机械设计与研究, 2019, 35(5): 11-14+23.
- 8. Selig, J. (2000) Geometrical Foundations of Robotics. World Scientific Publishing Co. Inc., Singapore. https://doi.org/10.1142/4257
- 9. 苏萌. 高速SCARA工业机器人的静态误差和动态误差模型研究[D]: [硕士学位论文]. 杭州: 浙江大学, 2012.
- 10. Murray, R.M., Sastry, S.S. and Zexiang, L. (1994) A Mathematical Introduction to Robotic Manipulation. CRC Press, Inc., Boca Raton.
- 11. 周炜. 飞机自动化装配工业机器人精度补偿方法与实验研究[D]: [博士学位论文]. 南京: 南京航空航天大学, 2012.
NOTES
*通讯作者。
