Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19067,12
pages
10.12677/AAM.2016.54080
Numerical Solution of Transmission Eigenvalue Problems of Helmholtz Equation
Xin Zhou, Tiexiang Li
Department of Mathematics, Southeast University, Nanjing Jiangsu

Received: Nov. 5th, 2016; accepted: Nov. 19th, 2016; published: Nov. 28th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we put forward a shift-and-invert algorithm to solve the transmission eigenvalue problem of Helmholtz equation, which can quickly and efficiently find out the several eigenvalues and the corresponding eigenvectors near arbitrarily given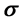 . First, we use the continuous finite element method to discrete the transmission eigenvalue problem of Helmholtz equation, and discrete the generalized eigenvalue problem into a quadratic eigenvalue problem, and then a new generalized eigenvalue problem is obtained by linearization. The new generalized eigenvalue problem eliminates the distraction of nonphysical zero eigenvalues, and preserves all the nonzero eigenvalues. Further through the use of shift-and-invert technology, we can quickly and efficiently get several real eigenpairs near given
. First, we use the continuous finite element method to discrete the transmission eigenvalue problem of Helmholtz equation, and discrete the generalized eigenvalue problem into a quadratic eigenvalue problem, and then a new generalized eigenvalue problem is obtained by linearization. The new generalized eigenvalue problem eliminates the distraction of nonphysical zero eigenvalues, and preserves all the nonzero eigenvalues. Further through the use of shift-and-invert technology, we can quickly and efficiently get several real eigenpairs near given . The proposed algorithm has no special restrictions to the refractive index of the transmission eigenvalue problems, that is to say, the refractive index can be positive or negative or positive and negative real numbers. The final numerical example verifies the effectiveness of our algorithm.
. The proposed algorithm has no special restrictions to the refractive index of the transmission eigenvalue problems, that is to say, the refractive index can be positive or negative or positive and negative real numbers. The final numerical example verifies the effectiveness of our algorithm.
Keywords:Transmission Eigenvalue, Generalized Eigenvalue Problem, Quadratic Eigenvalue Problem, Linearization, Shift-and-Invert

Helmholtz方程透射特征值问题的数值算法
周欣,李铁香
东南大学数学系,江苏 南京

收稿日期:2016年11月5日;录用日期:2016年11月19日;发布日期:2016年11月28日

摘 要
本文中我们对Helmholtz方程透射特征值问题提出一种带位移求逆的算法,此算法可以快速有效地求出任意给定的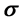 附近的几个实特征值及对应的特征向量。首先,我们用连续有限元方法对Helmholtz方程透射特征值问题进行离散,并将离散后的广义特征值问题化为一个二次特征值问题,进而对其进行线性化得到一个新的广义特征值问题。这个新的广义特征值问题排除了没有物理意义的零特征值的干扰,保留了所有的非零特征值。我们还利用位移求逆的技术,求得给定的
附近的几个实特征值及对应的特征向量。首先,我们用连续有限元方法对Helmholtz方程透射特征值问题进行离散,并将离散后的广义特征值问题化为一个二次特征值问题,进而对其进行线性化得到一个新的广义特征值问题。这个新的广义特征值问题排除了没有物理意义的零特征值的干扰,保留了所有的非零特征值。我们还利用位移求逆的技术,求得给定的 附近的几个实特征对。我们所提出的算法对透射特征值问题的折射率没有特别的限制,即折射率可为正或负亦或是任意的实函数。最后的数值算例验证了该算法的有效性。
附近的几个实特征对。我们所提出的算法对透射特征值问题的折射率没有特别的限制,即折射率可为正或负亦或是任意的实函数。最后的数值算例验证了该算法的有效性。
关键词 :透射特征值,广义特征值问题,二次特征值问题,线性化,位移求逆

1. 引言
本文中,我们将考虑声波在一个有界单连通的各向同性介质 上的Helmholtz方程透射特征值问题,即求解
上的Helmholtz方程透射特征值问题,即求解 并且
并且 满足方程
满足方程
 (1)
(1)
其中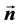 是单位外法向量,
是单位外法向量,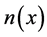 表示折射率,这里使得(1)有非平凡解
表示折射率,这里使得(1)有非平凡解 和
和 的非零的
的非零的 叫做透射特征值,相应的
叫做透射特征值,相应的 称为特征函数,我们称
称为特征函数,我们称 为特征对。
为特征对。
内部透射特征值问题来源于波场在非均匀介质中的逆散射理论,最早是由Colton和Monk提出 [1] ,是由一系列定义在散射物体上的方程构成的边值问题。尤其值得关注的是这类边值问题所对应的特征值问题,也就是透射特征值问题。由于透射特征值问题是一类非线性并且非自伴的特征值问题,所以椭圆方程的特征值问题的一些标准理论对其并不适用。在很长的一段时间内,关于透射特征值问题的研究都主要集中于证明透射特征值至多形成一个离散的集合 [2] 。从实际应用的角度出发,这个问题的离散性很重要,因为当入射频率恰好等于透射特征值时,用采样方法来重构非均匀介质的支集会失败 [3] 。另一方面,由于透射特征值问题的非自伴性,从20世纪80年代末透射特征值问题的提出 [1] ,一直到其后的20年中,非球形分层介质中透射特征值的存在性都是一个开放性的问题 [4] 。近年来,越来越多的学者开始关注透射特征值问题的研究,它也成为当今逆散射理论研究的重点之一 [5] 。在2010年 [6] 将透射特征值的存在性的理论进一步完善,证明了当折射率有界不变号并且不为0时,透射特征值存在一个无限集。 [7] 证明了透射特征值可以由散射场数据来决定,由于它们可以提供散射物体的一些性质,因此在一系列的目标识别问题中都扮演着很重要的作用。
自从 [4] 出现以来,越来越多的学者开始关注透射特征值问题的研究,它也成为当今逆散射理论研究的重点之一。目前,关于透射特征值问题的研究主要集中在以下三个方面:透射特征值的存在性以及透射特征值的估计;建立透射特征值问题的离散模型;对透射特征值问题离散模型的高效能计算。
关于透射特征值的存在性在 [3] 中已经给出了当折射率不变号且不为0时的证明,此外, [6] 也给出了对于最小的实数透射特征值的下界估计。Sun等针对透射特征值问题提出了不同的离散的方法 [8] [9] [10] ,这些方法将透射特征值问题(1)离散为一个广义特征值问题,值得注意的是此广义特征值问题具有大量的无物理意义的零特征值。 [11] [12] 充分利用有限元方法离散得到的质量矩阵、刚度矩阵的结构特点,利用矩阵变换的技巧将该离散后的广义特征值问题化为一个二次特征值问题,此二次特征值问题不再具有零特征值。针对 为正的情况, [12] 给出了一种能够快速有效计算几个最小正实特征值的割线法,但此割线法只适用于
为正的情况, [12] 给出了一种能够快速有效计算几个最小正实特征值的割线法,但此割线法只适用于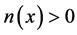 的情况。
的情况。
而事实上目前一些人工的复合材料能够实现 取负值或既有正值也有负值的情况,因此本文中我们将考虑
取负值或既有正值也有负值的情况,因此本文中我们将考虑 不一定恒为正的情况,并提出一种可以求解任意给定位置附近的特征值以及对应的特征向量的算法。首先我们利用连续有限元方法来对Helmholtz透射特征值问题(1)进行离散,将离散后得到的广义特征值问题进一步化为没有零特征值的二次特征值问题,再对得到的二次特征值问题进行线性化,得到一个新的广义特征值问题,此广义特征值问题不再具有零特征值。我们利用位移求逆的技术给出了一个普遍适用的求解透射特征值问题的方法,通过将得到的特征值以及对应的特征向量带回到原二次特征值问题中检查相应的残量,来验证我们的算法的有效性。该方法可以对任意给定的
不一定恒为正的情况,并提出一种可以求解任意给定位置附近的特征值以及对应的特征向量的算法。首先我们利用连续有限元方法来对Helmholtz透射特征值问题(1)进行离散,将离散后得到的广义特征值问题进一步化为没有零特征值的二次特征值问题,再对得到的二次特征值问题进行线性化,得到一个新的广义特征值问题,此广义特征值问题不再具有零特征值。我们利用位移求逆的技术给出了一个普遍适用的求解透射特征值问题的方法,通过将得到的特征值以及对应的特征向量带回到原二次特征值问题中检查相应的残量,来验证我们的算法的有效性。该方法可以对任意给定的 附近的几个特征值和对应的特征向量进行求解。
附近的几个特征值和对应的特征向量进行求解。
本文中 表示
表示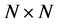 的单位矩阵,对矩阵
的单位矩阵,对矩阵 ,
, 表示
表示 是对称正定的,
是对称正定的, 表示矩阵或者向量的转置。
表示矩阵或者向量的转置。
2. 透射特征值的离散
2.1. 连续有限元方法
用标准的分段线性有限元方法来离散透射特征值问题(1) [2] 。令
 上连续的分段线性函数构成的空间,
上连续的分段线性函数构成的空间,
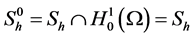 的子空间且在
的子空间且在 上取值为0,
上取值为0,
 的子空间且在
的子空间且在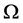 内的自由度为0。
内的自由度为0。
对于系统(1),我们要寻求一种有限元近似。令
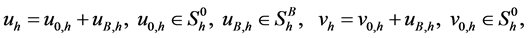
其中, 是
是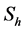 空间上一个一般的函数,
空间上一个一般的函数,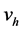 的选取满足在
的选取满足在 上
上 成立,也就是使得(1c)恒成立。令
成立,也就是使得(1c)恒成立。令 ,分别取测试函数
,分别取测试函数 ,
, ,
, 作用于系统(1),则可以得到
作用于系统(1),则可以得到
 (2)
(2)
令 表示有限元空间
表示有限元空间 的一组基,其中
的一组基,其中 表示网格划分后内部节点的个数,
表示网格划分后内部节点的个数, 表示有限元空间
表示有限元空间 的一组基,其中
的一组基,其中 表示网格划分后边界节点的个数,于是
表示网格划分后边界节点的个数,于是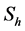 的一组基可以表示为
的一组基可以表示为 。记
。记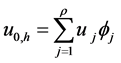 ,
, ,
,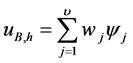 。
。
下面定义本文中要用到的刚度矩阵和质量矩阵,见表1。
Table 1. The definition of stiffness matrix and mass matrix
表1. 刚度矩阵和质量矩阵的定义
根据刚度矩阵和质量矩阵的定义,方程组(2)等价于

因此,透射特征值问题(1)被离散为广义特征值问题
 ,(3)
,(3)
其中

2.2. 将广义特征值问题化为二次特征值问题
本节中我们将参考 [12] [13] [14] 中的技巧,利用表1中刚度矩阵和质量矩阵的结构特点对广义特征值问题(3)进行一系列的矩阵变换,将其化为一个二次特征值问题。为了方便起见,我们定义如下符号。记

在 和
和 两端同时左乘初等变换矩阵
两端同时左乘初等变换矩阵
 ,
,
右乘初等变换矩阵
 ,
,
原广义特征值问题(3)等价于
 , (4)
, (4)
其表示为矩阵的形式即为:
 。
。
我们将向量 都通过向量
都通过向量 来表示,并且分别用
来表示,并且分别用 和
和 来替换
来替换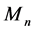 和
和 ,同时根据
,同时根据 的次数将带有
的次数将带有 和
和 的项组合起来,得到一个关于
的项组合起来,得到一个关于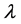 的二次方程,即
的二次方程,即

其中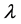 的二次项系数为
的二次项系数为
 ,
,
 的一次项系数为
的一次项系数为
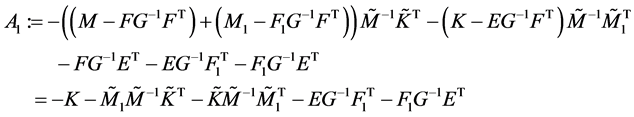
常数项为

这样,广义特征值问题(4)被转化为一个关于 的二次特征值问题:
的二次特征值问题:
 。 (5)
。 (5)
3. 二次特征值问题的求解
由表1中刚度矩阵和质量矩阵的定义,我们知道 ,且二次特征值问题(5)的系数矩阵
,且二次特征值问题(5)的系数矩阵 是对称的。当
是对称的。当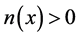 时,
时, ,可以推出
,可以推出 和
和 对称正定,割线法 [12] 正是利用了
对称正定,割线法 [12] 正是利用了 和
和 对称正定的性质来求几个最小的正实特征值。当
对称正定的性质来求几个最小的正实特征值。当 不恒为正时,矩阵
不恒为正时,矩阵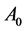 和
和 不能保证是对称正定的,因此割线法就不再适用。本文中我们将给出一种不依赖于矩阵对称正定的性质来求解二次特征值问题(5)的方法,且不再只是求解几个最小的正实特征值,而是可以求解任意位置附近的特征值以及对应的特征向量。
不能保证是对称正定的,因此割线法就不再适用。本文中我们将给出一种不依赖于矩阵对称正定的性质来求解二次特征值问题(5)的方法,且不再只是求解几个最小的正实特征值,而是可以求解任意位置附近的特征值以及对应的特征向量。
我们通过线性化 [15] [16] 将二次特征值问题(5)转化为等价的广义特征值问题
 。 (6)
。 (6)
一方面,原广义特征值问题(3)是 的,而新得到的广义特征值问题(6)是
的,而新得到的广义特征值问题(6)是 的,规模已经变小;另一方面,二次特征值问题(5)已经排除了没有物理意义的零特征值的干扰,转化为等价的广义特征值问题(6)后同样没有零特征值。接下来我们将通过位移求逆的技术,来求得任意给定的
的,规模已经变小;另一方面,二次特征值问题(5)已经排除了没有物理意义的零特征值的干扰,转化为等价的广义特征值问题(6)后同样没有零特征值。接下来我们将通过位移求逆的技术,来求得任意给定的 附近的几个实特征值和对应的特征向量。
附近的几个实特征值和对应的特征向量。
令
 。 (7)
。 (7)
则广义特征值问题(6)可表示为 。通常
。通常 和
和 比较大,虽然方程(1)离散后得到的刚度矩阵和质量矩阵是稀疏的,但是如果直接由
比较大,虽然方程(1)离散后得到的刚度矩阵和质量矩阵是稀疏的,但是如果直接由 的定义将它们乘在一起就会使得
的定义将它们乘在一起就会使得 变得稠密,所以通常
变得稠密,所以通常 和
和 都是无法直接给出的。
都是无法直接给出的。
为利用位移求逆的技术 [17] ,我们将考虑特征值问题
 , (8)
, (8)
其中 是任意给定的数值。
是任意给定的数值。
3.1. 求解线性方程组
本节我们考虑如何在 无法直接给出的情况下求解线性方程组
无法直接给出的情况下求解线性方程组 。根据
。根据 的分块结构,可以看出求解线性方程组
的分块结构,可以看出求解线性方程组 ,其中
,其中 ,
,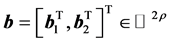 为任意给定的向量,相当于求解如下方程组
为任意给定的向量,相当于求解如下方程组
 (9)
(9)
从(9)我们发现,要求解线性方程组 关键是要求解
关键是要求解 。
。
下面我们考虑如何在 无法直接给出的情况下求解线性方程组
无法直接给出的情况下求解线性方程组 。由于
。由于
 , (10)
, (10)
我们令 ,
, ,
,
则 ,且求解
,且求解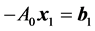 等价于求解
等价于求解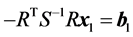 。利用分块Gauss消去法有
。利用分块Gauss消去法有
 , (11)
, (11)
由于矩阵 是稀疏的,线性方程组
是稀疏的,线性方程组
 , (12)
, (12)
可以直接通过左除求得
 。(13)
。(13)
在(12)两端同时左乘 得到
得到
 (14)
(14)
因此可以得到(9)中的 即为(14)中
即为(14)中 。换句话说,我们可以通过求解(12)来得到
。换句话说,我们可以通过求解(12)来得到 的解。
的解。
3.2. 求解任意位置的特征对
本节我们考虑对任意给定的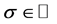 ,如何求解广义特征值问题(6)在
,如何求解广义特征值问题(6)在 附近的
附近的 个特征值及对应的特征向量。这个问题等价于求解带位移
个特征值及对应的特征向量。这个问题等价于求解带位移 的广义特征值问题(8)。我们考虑利用MATLAB中的命令
的广义特征值问题(8)。我们考虑利用MATLAB中的命令 来求解此问题。
来求解此问题。
当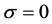 时,求解广义特征值问题(8)等价于求
时,求解广义特征值问题(8)等价于求 的
的 个模最大的特征值及对应的特征向量。我们利用命令
个模最大的特征值及对应的特征向量。我们利用命令 ,其中函数
,其中函数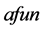 要求返回矩阵
要求返回矩阵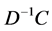 与给定的向量
与给定的向量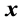 相乘的结果
相乘的结果 ,其中
,其中 等价于3.1节中的求解线性方程组
等价于3.1节中的求解线性方程组 。
。
当 时,带位移
时,带位移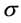 的广义特征值问题(8)等价于
的广义特征值问题(8)等价于
 , (15)
, (15)
所以有 。由定义(7)知
。由定义(7)知
 ,(16)
,(16)
利用分块Gauss消去法将(16)消为上三角矩阵
 ,
,
可以推出
 。
。
因此,特征值问题(15)等价于
 。 (17)
。 (17)
为方便起见,对二次特征值问题(5)的系数矩阵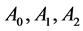 做如下变形:
做如下变形:

对任意给定的 ,有
,有

记

所以(17)等价于
 。 (18)
。 (18)
我们利用命令 求解(18),其中函数
求解(18),其中函数 要求返回矩阵
要求返回矩阵 与给定的向量
与给定的向量 相乘的结果
相乘的结果 。
。
因为
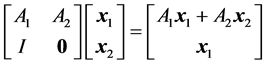 ,
,
 ,
,
 。 (19)
。 (19)
结合(17),可以看出求解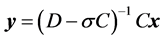 ,关键是要求解
,关键是要求解 ,其中
,其中
 (20)
(20)
因为 ,若
,若 满足
满足
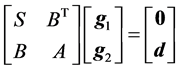
则有
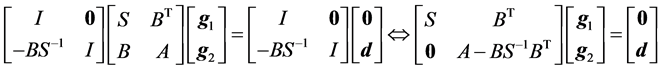 ,
,
即 。
。
与3.1节中的技巧类似。 可以直接通过
可以直接通过 求得,即求得
求得,即求得 的解。将此结果带入到(19)中,即可得到函数
的解。将此结果带入到(19)中,即可得到函数 的定义,再利用命令
的定义,再利用命令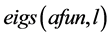 即可求解特征值问题(17)。
即可求解特征值问题(17)。
4. 数值结果
本文中我们考虑以下三种数学模型 [18] ,分别是1) 以原点为圆心的单位圆,2) 以原点为中心的边长为2的正方形,3) 以原点为中心长半轴长为2短半轴长为1的椭圆这三种区域,取网格大小 ,利用2.1节中连续有限元方法,在这三种区域上对透射特征值问题(1)进行离散。
,利用2.1节中连续有限元方法,在这三种区域上对透射特征值问题(1)进行离散。

给定 ,我们将分别计算4个最小的正实透射特征值及相应的残量或离给定的
,我们将分别计算4个最小的正实透射特征值及相应的残量或离给定的 最近的4个特征值及相应的残量。
最近的4个特征值及相应的残量。
4.1. 最小的正实透射特征值
4.1.1. 为常数
为常数
本节考虑 取常数的情况,我们将计算透射特征值问题(1)的4个最小的正实特征值及相应的残量。利用3.2节中的介绍的
取常数的情况,我们将计算透射特征值问题(1)的4个最小的正实特征值及相应的残量。利用3.2节中的介绍的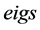 的方法求解广义特征值问题(6),表2和表3分别给出了
的方法求解广义特征值问题(6),表2和表3分别给出了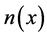 为4和−4所对应的4个最小的正实透射特征值
为4和−4所对应的4个最小的正实透射特征值 和对应的特征向量
和对应的特征向量 以及将它们带回到二次特征值问题(5)中所得到的残量,
以及将它们带回到二次特征值问题(5)中所得到的残量,
 。
。
取 的无穷模范数
的无穷模范数 做为误差的估计。通过表2和表3我们可以看出,当
做为误差的估计。通过表2和表3我们可以看出,当 为常数时本文中提出的算法是准确有效的。
为常数时本文中提出的算法是准确有效的。
4.1.2. 非常数
非常数
本节考虑 为非常数的情况,我们将计算透射特征值问题(1)的4个最小的正实特征值及相应的误差。利用3.2节中的介绍的
为非常数的情况,我们将计算透射特征值问题(1)的4个最小的正实特征值及相应的误差。利用3.2节中的介绍的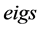 的方法求解广义特征值问题(6),首先考虑
的方法求解广义特征值问题(6),首先考虑 有正有负的情况,设
有正有负的情况,设 ,即每个点的横坐标与纵坐标的差,表4给出了此时不同区域所对应的4个最小的正实透
,即每个点的横坐标与纵坐标的差,表4给出了此时不同区域所对应的4个最小的正实透
射特征值以及相应的误差。表5给出了 为分段函数的情况,如下图所示,
为分段函数的情况,如下图所示, ,不同区域
,不同区域
所对应的4个最小的正实透射特征值以及对应的误差。
4.2. 位移求逆
本节我们考虑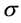 不为0的情况,利用3.2节中给出的
不为0的情况,利用3.2节中给出的 的方法求解特征值问题(18)。表6给出了
的方法求解特征值问题(18)。表6给出了
Table 2. When, four smallest real transmission eigenvalues and their error of different domains
表2.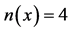 时不同区域所对应的4个最小的正实透射特征值以及相应的误差
时不同区域所对应的4个最小的正实透射特征值以及相应的误差
Table 3. When, four smallest real transmission eigenvalues and their error of different domains
表3. 时不同区域所对应的4个最小的正实透射特征值以及相应的误差
时不同区域所对应的4个最小的正实透射特征值以及相应的误差
Table 4. When, four smallest real transmission eigenvalues and their error of different domains
表4. 时不同区域所对应的4个最小的正实透射特征值以及相应的误差
时不同区域所对应的4个最小的正实透射特征值以及相应的误差
Table 5. When, four smallest real transmission eigenvalues and their error of different domains
表5. 时不同区域所对应的4个最小的正实透射特征值以及相应的误差
时不同区域所对应的4个最小的正实透射特征值以及相应的误差
Table 6. When, four real transmission eigenvalues near 10 and their error of different domains
表6.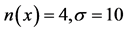 时不同区域所对应的离10最近的4个正实透射特征值以及相应的误差
时不同区域所对应的离10最近的4个正实透射特征值以及相应的误差
 时离
时离 最近的4个实透射特征值以及相应的误差。
最近的4个实透射特征值以及相应的误差。
通过表6可以看出,本文中给出的位移求逆技术来计算离 最近的几个实特征值以及对应的特征向量是切实有效的。我们也可以通过逐步修正
最近的几个实特征值以及对应的特征向量是切实有效的。我们也可以通过逐步修正 的值的方式,利用位移求逆技术,得到某个区间上的全部实特征值。
的值的方式,利用位移求逆技术,得到某个区间上的全部实特征值。
5. 总结
本文中我们利用连续有限元方法对透射特征值问题(1)进行离散,将得到的广义特征值问题(3)化为没有零特征干扰的二次特征值问题(5),进而再通过对(5)线性化得到一个新的广义特征值问题(6)。对新得到的广义特征值问题(6)我们提出了一种带位移求逆的算法,可以计算透射特征值问题(1)的几个最小的正实特征值及对应的特征向量,也可以快速有效地求出任意给定的 附近的几个实特征值及对应的特征向量。本文中的算法是基于这样一个事实,即当系数矩阵为稀疏矩阵时,线性方程组的解可以通过直接对系数矩阵进行左除得到。实际上,本文所设计的算法也适用于计算任意给定的
附近的几个实特征值及对应的特征向量。本文中的算法是基于这样一个事实,即当系数矩阵为稀疏矩阵时,线性方程组的解可以通过直接对系数矩阵进行左除得到。实际上,本文所设计的算法也适用于计算任意给定的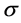 附近的复特征值及对应的特征向量,也可以通过不断地修正
附近的复特征值及对应的特征向量,也可以通过不断地修正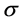 的值的方式,求出某个区间或某个区域上的全部特征值,进而了解透射特征值的分布情况。
的值的方式,求出某个区间或某个区域上的全部特征值,进而了解透射特征值的分布情况。
致谢
本文得到国家自然基金(11471074)资助。
文章引用
周欣,李铁香. Helmholtz方程透射特征值问题的数值算法
Numerical Solution of Transmission Eigenvalue Problems of Helmholtz Equation[J]. 应用数学进展, 2016, 05(04): 683-694. http://dx.doi.org/10.12677/AAM.2016.54080
参考文献 (References)
- 1. Colton, D. and Monk, P. (1988) The Inverse Scattering Problem for Time Hormonic Acoustic Waves in an Inhomogeneous Meium. The Quarterly Journal of Mechanics and Applied Mathematics, 41, 97-125. https://doi.org/10.1093/qjmam/41.1.97
- 2. Cakoni, F., Gintides, D. and Monk, P. (2007) On the Use of Transmission Eigenvalues to Estimate the Index of Refraction from Far Field Data. Inverse Problems, 23, 507-522. https://doi.org/10.1088/0266-5611/23/2/004
- 3. Cakoni, F. and Gintides, D. (2006) Qualitative Methods in Inverse Scattering Theory: An Introduction, Interaction of Mechanics and Mathematics. Springer. Berlin.
- 4. Päivärinta, L. and Sylvester, L. (2008) Transmission Eigenvalues. SIAM Journal on Mathematical Analysis, 40, 738-753. https://doi.org/10.1137/070697525
- 5. Cakoni, F. and Gintides, D. (2010) New Results on Transmission Eigenvalues. Inverse Problem and Imaging, 4, 39-48. https://doi.org/10.3934/ipi.2010.4.39
- 6. Cakoni, F., Gintides, D. and Haddar, H. (2010) The Existence of an Infinite Discrete Set of Transmission Eigenvalues. SIAM Journal on Mathematical Analysis, 42, 237-255. https://doi.org/10.1137/090769338
- 7. Cakoni, F., Gintides, D. and Haddar, H. (2010) On the Determination of Dirichlet or Transmission Eigenvalued from Far Field Data. Comptes Rendus Mathematique, 348, 379-383. https://doi.org/10.1016/j.crma.2010.02.003
- 8. Colton, D., Monk, P. and Sun, J. (2010) Analytical and Computational Methods for Transmission Eigenvalues. Inverse Problems, 26, 045011. https://doi.org/10.1088/0266-5611/26/4/045011
- 9. Ji, X., Sun, J. and Xie, H. (2014) A Multigrid Method for Helmholtz Transmission Eigenvalues Problems. Journal of Scientific Computing, 60, 276-294. https://doi.org/10.1007/s10915-013-9794-9
- 10. Ji, X., Sun, J. and Turner, T. (2012) A Mixed Finite Element Method for Helmholtz Transmission Eigenvalues. ACM Transactions on Mathematical Software, 38, Article No. 29.
- 11. Huang, T.-M., Huang, W.-Q. and Lin, W.-W. (2015) A Robust Numerical Algorithm for Computing Maxwell’s Transmission Eigenvalue Problems. SIAM Journal on Scientific Computing, 37, A2403-A2423. https://doi.org/10.1137/15M1018927
- 12. Li, T., Huang, W.-Q., Lin, W.-W. and Liu, J. (2015) On Spectral Analysis and a Novel Algorithm for Transmission Eigenvalue Problems. Journal of Scientific Computing, 64, 83-108. https://doi.org/10.1007/s10915-014-9923-0
- 13. Moler, C.B. and Stewart, G.W. (1973) An Algorithm for Generalized Matrix Eigenvalue Problems. SIAM Journal on Numerical Analysis, 10, 241-256. https://doi.org/10.1137/0710024
- 14. Parlett, B.N. (1998) The Symmetric Eigenvalue Problem. SIAM, Philadelphia. https://doi.org/10.1137/1.9781611971163
- 15. Guo, J.S., Lin, W.W. and Wang, C.S. (1995) Numerical Solutions for Large Sparse Quadratic Eigenvalue Problems. Linear Algebra and its Applications, 225, 57-89. https://doi.org/10.1016/0024-3795(93)00318-T
- 16. Tisseur, F. and Meerbergen, K. (2001) The Quadratic Eigenvalue Problem. SIAM Review, 43, 235-286. https://doi.org/10.1137/S0036144500381988
- 17. Golub, G.H. and Van Loan, C.F. (2012) Matrix Computations. 4th Edition, The Johns Hopkins University Press, Baltimore.
- 18. Persson, P.O. and Strang, G. (2004) A Simple Mesh Generator in Matlab. SIAM Review, 46, 329-345. https://doi.org/10.1137/S0036144503429121



