Advances in Applied Mathematics
Vol.06 No.04(2017), Article ID:21436,6
pages
10.12677/AAM.2017.64063
The Global Existence and Blow-Up Conditions for a Class of Nonlinear Degenerate Hyperbolic Equation
Jialing Zhu
College of Mathematics, Southwest Jiaotong University, Chengdu Sichuan

Received: Jul. 1st, 2017; accepted: Jul. 17th, 2017; published: Jul. 20th, 2017

ABSTRACT
In this paper, the initial-boundary value problem for a class of degenerate hyperbolic equation is studied. The global existence of solution is obtained by introducing Galerkin method. Also the global nonexistence of solution can be verified by using the analysis method while the initial energy is positive and bounded.
Keywords:Degenerate Hyperbolic Equation, Galerkin Method, Global Solutions, Blow Up
一类非线性退化双曲方程解的整体存在性和爆破的条件
祝佳玲
西南交通大学数学学院,四川 成都
收稿日期:2017年7月1日;录用日期:2017年7月17日;发布日期:2017年7月20日

摘 要
本文研究了一类非线性退化双曲方程的初边值问题。借助Galerkin方法得到了解的整体存在性,与此同时,当初始能量为正且有界时,通过分析的方法可以证明解爆破。
关键词 :退化双曲方程,Galerkin方法,整体解,爆破

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文研究了如下非线性退化双曲方程的初边值问题
 (1.1)
(1.1)
其中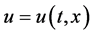 是复值函数,
是复值函数, 为边界充分光滑的有界区域,
为边界充分光滑的有界区域, 为退化的椭圆型算子。
为退化的椭圆型算子。
方程(1.1)常用来研究弹塑性杆中纵向运动的微观结构模型的弱非线性问题。与问题(1.1)相关的半线性波动方程的初边值问题已被许多学者进行了广泛的研究,如文献 [1] - [6] 。其中John [1] 和Glassey [2] 研究了柯西问题
 (1.2)
(1.2)
证明了解整体存在和爆破的条件。他们发现了非线性项的指数增长控制与空间维数有严格的关系,即在小初值下,给定有限充分小的正数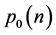 (称
(称 依赖于
依赖于 ),存在数
),存在数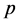 ,使得若
,使得若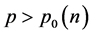 ,则解整体存在;若
,则解整体存在;若 ,则解爆破. Ye Yaojun [3] 是 [1] 的推广情形,即研究了如下非线性退化双曲方程的初边值问题
,则解爆破. Ye Yaojun [3] 是 [1] 的推广情形,即研究了如下非线性退化双曲方程的初边值问题
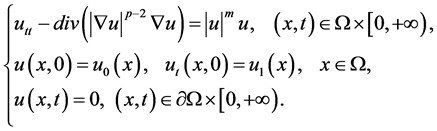 (1.3)
(1.3)
Ye [3] 采采用了Galerkin方法证明了解的整体存在性,并通过分析的方法得到了解爆破的条件. 本文是问题(1.3)的一个简化模型。
由于Ye [3] 中椭圆型算子项和非线性项的指数不确定,所以在证明势井深度的正性和进行能量估计时过程繁杂,而本文采用与Ye [3] 类似的方法可经过简单精妙的估计得到解整体存在和爆破的条件,这也是本文的主要创新。
2. 势井深度
对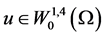 ,定义如下能量泛函:
,定义如下能量泛函:
 (2.1)
(2.1)
定义稳定集
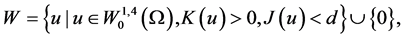 (2.2)
(2.2)
其中

且
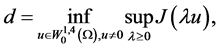
为势井深度。
下面将证明 始终大于0,即有如下引理:
始终大于0,即有如下引理:
引理2.2 假设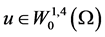 ,则
,则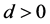 。
。
证明 因为
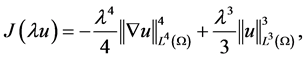

则

当 时,经计算
时,经计算
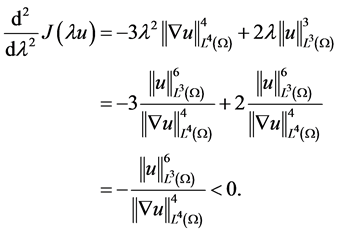
因此有

即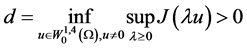 。
。
3. 解整体存在和爆破的条件
为了得到解整体存在和爆破的条件,有如下准备引理:
引理3.1 [3] 令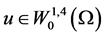 ,假设1) 当
,假设1) 当 ,
,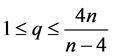 ;2) 当
;2) 当 ,
,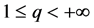 ,则
,则 ,
, ,其中
,其中 为常数,
为常数,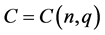 。
。
记能量
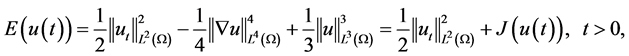 (3.1)
(3.1)
初始能量
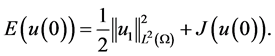 (3.2)
(3.2)
首先研究当初始能量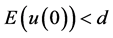 时解整体存在的条件,采用的方法是Galerkin方法,证明过程是常规步骤的实施,本文只给出相应的先验估计。
时解整体存在的条件,采用的方法是Galerkin方法,证明过程是常规步骤的实施,本文只给出相应的先验估计。
定理3.2 若 ,
,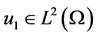 ,
,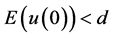 ,则问题(1.1)存在整体解
,则问题(1.1)存在整体解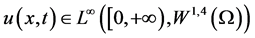 ,
,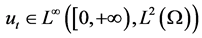 。
。
证明 方程(1.1)乘以 在
在 上积分得
上积分得
 (3.3)
(3.3)
由(3.3)需证
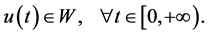 (3.4)
(3.4)
假设上式不成立,则令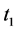 是使得
是使得 的最小时间。由
的最小时间。由 的连续性,知
的连续性,知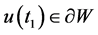 。由
。由 的定义及
的定义及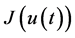 和
和 关于
关于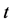 连续,则
连续,则
 (3.5)
(3.5)
或
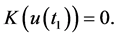 (3.6)
(3.6)
由(3.3)和条件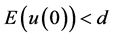 ,知
,知
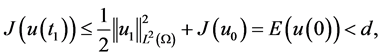
所以(3.5)式不成立。
又假设(3.6)式成立,则


上式和 的定义矛盾,因此(3.6)式也不成立。
的定义矛盾,因此(3.6)式也不成立。
由(3.3)和(3.5)有
 (3.7)
(3.7)
由(3.7)有

所以 ,
,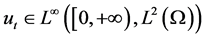 。
。
其次研究当初始能量为正且恰当有界时,解爆破。
定理3.3 假设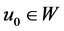 ,
,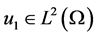 ,若初值使得
,若初值使得
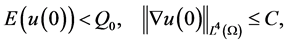
其中 ,
,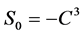 ,
, 是正的Sobolev常数,则问题(1.1)不存在整体解,即解爆破。
是正的Sobolev常数,则问题(1.1)不存在整体解,即解爆破。
证明 假设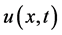 是问题(1.1)的整体解,则有引理3.1知,存在常数
是问题(1.1)的整体解,则有引理3.1知,存在常数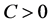 ,
,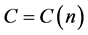 ,对所有的
,对所有的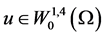 ,有
,有
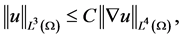 (3.8)
(3.8)
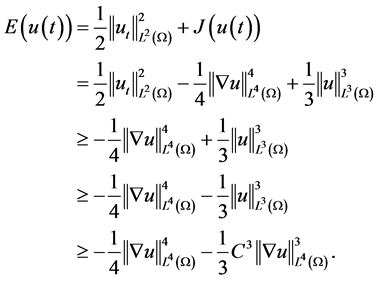 (3.9)
(3.9)
令

记(3.9)式右边为
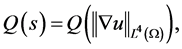
则
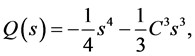 (3.10)
(3.10)
由(3.10)得 。
。
令 ,得
,得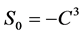 。当
。当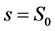 时,有
时,有
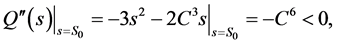
所以函数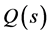 在
在 处有最大值
处有最大值
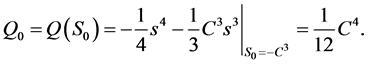
因为初值使得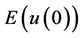 ,
, 满足
满足
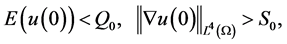
因此由能量守恒有

由(3.9)和(3.10)知不存在时间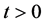 ,使得
,使得
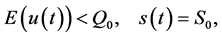
因此由 和
和 的连续性得
的连续性得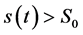 对所有的
对所有的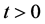 成立。由以上矛盾知(1.1)不存在整体解,即解在有限时间内爆破。
成立。由以上矛盾知(1.1)不存在整体解,即解在有限时间内爆破。
文章引用
祝佳玲. 一类非线性退化双曲方程解的整体存在性和爆破的条件
The Global Existence and Blow-Up Conditions for a Class of Nonlinear Degenerate Hyperbolic Equation[J]. 应用数学进展, 2017, 06(04): 523-528. http://dx.doi.org/10.12677/AAM.2017.64063
参考文献 (References)
- 1. John, F. (1979) Blow-Up of Solutions of Nonlinear Wave Equations. Manuscripta Mathematica, 76, 235-268. https://doi.org/10.1007/BF01647974
- 2. Glassey, R. (1981) Finite-Time Blow-Up for Solutions of Nonlinear Wave Equations. Mathematische Zeitschrift, 177, 323-340. https://doi.org/10.1007/BF01162066
- 3. Ye, Y.J. (2005) Existence and Nonexistence of Global Solutions of the Initial-Boundary Value Problem for Some Degenerate Hyperbolic Equation. Journal of Mathematical Physics, 25, 703-709.
- 4. 张健. 一个退化双曲方程的初边值问题[J]. 四川师范大学学报, 1993, 16(2): 43-46.
- 5. 管楚洤. 非线性退化双曲方程的Cauchy问题[J]. 科学通报, 1982, 1982(23): 1409-1413.
- 6. Yang, X.F. (2006) Lower Bounds on Life-Span of Classical Solution to Quasi-Linear Hyperbolic Systems. Journal of Mathematics, 26, 237-242.