Advances in Applied Mathematics
Vol.06 No.09(2017), Article ID:23135,5
pages
10.12677/AAM.2017.69139
Numerical Analysis of Backward Euler-Galerkin Method for Water Contamination Problem
Nazakat Adil, Emam Mamat, Abdirixit Abduwali*
College of Mathematics and Systems Science, Xinjiang University, Urumqi Xinjiang

Received: Nov. 29th, 2017; accepted: Dec. 15th, 2017; published: Dec. 22nd, 2017

ABSTRACT
The Galerkin finite element method for the diffusion of water contamination is analyzed. The time variable is discretized by backward Euler method. Finally, we did numerical simulations with a concrete example.
Keywords:Water Contamination Diffusion Equation, Galerkin Finite Element Method, Backward Euler Method
水污染问题的向后Euler-Galerkin 方法及数值模拟
娜扎开提·阿迪力,伊马木·麦麦提,阿布都热西提·阿布都外力*
新疆大学数学与系统科学学院,新疆 乌鲁木齐
收稿日期:2017年11月29日;录用日期:2017年12月15日;发布日期:2017年12月22日

摘 要
分析了浅水流动中的水污染扩散问题的Galerkin有限元方法,对于时间变量用向后Euler法进行离散。最后通过具体例子进行了数值模拟。
关键词 :水污染扩散方程,Galerkin有限元方法,向后Euler法

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
浅水流中的污染物扩散问题有比较重要的实用价值。在相对较浅的自由表面流动中,水平速度为主要分量,问题可以适当的近似为二维问题。Navier-Stokes方程是流体力学中的基本方程,因此可当该方程为出发点,应用沿深度积分的方法可得到浅水流方程 [1] 。浅水流作为污染物运输的载体,可以写出一种污染物扩散问题的方程 [1] :
(1)
其中C为污染物浓度;Q为源项; 、 分别为x、y方向的扩散系数;H为水深; 、 分别为流速在x、y方向的分量。水深与流速可由浅水流方程确定,本文的数值例子中将它们预先给出。
利用深度平均的连续守恒方程
将(1)式进一步改写成
其中 , 。
王焕焕和冯新龙 [2] 分析了水污染扩散问题的两种有限差分格式,证明了其相容性、稳定性与收敛性。王焕 [3] 研究了该问题的特征有限元方法,得到了 误差和 误差估计。
为简便,本文中以图1所示的河的示意图为例,假设河内没有污染源。令扩散系数 (常数)。假设 与边界中的污染源充分远,可认为污染物浓度在研究的时间段内为零, 是河岸。因此问题可写成
2. 向后Euler-Galerkin有限元形式
本文使用下列空间,对于非负整数 和实数 ,定义
[4]
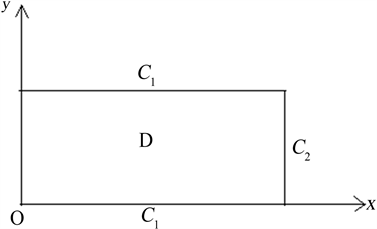
Figure 1. Diagram of the river
图1. 河的形状示意图
在此空间上定义范数如下:
当 时,记 为 ,相应的范数为 。
现在推导(2)~(5)的变分形式。记 ,用函数 与方程(2)的两端做内积
因此(2)~(5)的变分形式为:求 ,使得
(6)
其中 为下式所定义的双线性形式
利用Green公式及(4)、(5)式可简化成
设 为 上的拟均匀剖分,网格参数 ,选取的有限元空间为
因此对于问题(2)~(5)的Galerkin有限元形式是:求 ,使得
(7)
其中 是 的某个近似。
现设 为空间 的基底,将未知函数 表示为
并在(7)中取 ,则有
(8)
其中 为 按基函数 展开的系数。
引进矩阵和向量记号: , , ,其中 , 。记M为质量矩阵,A为刚度矩阵。借助上述记号,可将(8)改写成
如果再对时间变量用有限元离散会使计算量有成量级的增加。因此在时间 上我们采用向后Euler差商,从而得到的全离散格式为
(9)
其中 为时间步长。
根据文献 [4] 可知,当有限元形式(7)中的初值 满足条件
时,相应的近似解 与变分形式(6)的真解 之间的误差估计为
易知全离散格式(9)对时间t是一阶精度的。
3. 数值实验
针对图1所示的河,考虑初边值问题(2)~(5)的数值计算。设 、k = 15 m2/s,初始条件为
为计算简便,将水深函数 取为
x轴方向20等分,y轴方向15等分便得到矩形单元,这里有限元空间取为
 (a) t = 100 s
(a) t = 100 s
 (b) t = 500 s
(b) t = 500 s
 (c) t = 1000 s
(c) t = 1000 s
 (d) t = 2000 s
(d) t = 2000 s
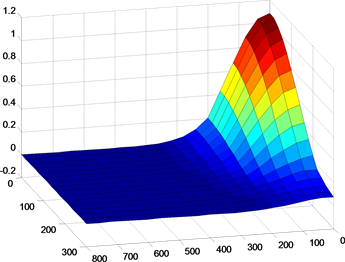
Figure 2. Distribution of the concentration of pollutants in the river with time
图2. 河中污染物浓度随时间变化的分布情况
取时间步长 ,用全离散格式(9)进行计算,就可以得到数值解。图2(a)~图2(d)给出了当时间
t =100 s;t = 500 s;t = 1000 s;t = 2000 s时河中污染物浓度分布情况,图中的高度表示浓度大小。
4. 结论
本文中推导出了水污染扩散问题的向后Euler-Galerkin方法。通过数值模拟的结果看到效果是较好的。
文章引用
娜扎开提·阿迪力,伊马木·麦麦提,阿布都热西提·阿布都外力. 水污染问题的向后Euler-Galerkin方法及数值模拟
Numerical Analysis of Backward Euler-Galerkin Method for Water Contamination Problem[J]. 应用数学进展, 2017, 06(09): 1146-1150. http://dx.doi.org/10.12677/AAM.2017.69139
参考文献 (References)
- 1. Zienkiewicz, O.C. and Taylor, R.L. 有限元方法. 第五版. 第三卷, 流体动力学[M]. 北京: 清华大学出版社, 2008.
- 2. 王焕焕, 冯新龙, 阿布都热西提. 水污染的二维数学模型的数值计算[J]. 吉林大学自然科学学报, 2001(2): 19-24.
- 3. 王焕. 水污染问题特征有限元方法的数值计算及理论分析[J]. 应用数学, 2003, 16(2): 42-49.
- 4. 应隆安, 陈传淼. 有限元理论与方法. 第二分册[M]. 北京: 科学出版社, 2009.