Advances in Applied Mathematics
Vol.
07
No.
12
(
2018
), Article ID:
28151
,
10
pages
10.12677/AAM.2018.712185
The Research of Special Clothing for High Temperature Operation
Yuting Wang, Haoran Qin, Guanghao Zhang, Kaisen Zhang
Shenyang Aerospace University, Shenyang Liaoning

Received: Nov. 23rd, 2018; accepted: Dec. 17th, 2018; published: Dec. 24th, 2018

ABSTRACT
In this paper, based on the design problem of high-temperature special clothing, the lumped parameter method and double-layer glass heat transfer model are used to establish the temperature distribution model, optimization model and temperature difference model of garment materials. Using MATLAB, LINGO and other software to solve the model, the relationship between temperature, time function and the optimal thickness of fabric material are obtained. Considering that the heat transfer method only considers the heat conduction, the compensation coefficient is defined to reduce the error of the model. This model provides a reliable basis for the design and cost control of special clothing for high temperature operation. This paper can also be used to predict the insulation effect of insulating glass and the insulation effect of buildings in winter. The accuracy of this paper is higher and the prediction results are accurate.
Keywords:Special Clothing for High Temperature Operation, Lumped Parameter Method, Difference Methods, Optimization
高温作业专用服装的研究
王玉婷,秦浩然,张广浩,张凯森
沈阳航空航天大学,辽宁 沈阳

收稿日期:2018年11月23日;录用日期:2018年12月17日;发布日期:2018年12月24日

摘 要
本文针对高温作业专用服装设计问题,运用集总参数法、双层玻璃传热模型,建立服装材料温度分布模型、最优化模型、温度差分模型。运用MATLAB、LINGO等软件进行模型求解,得出温度与时间函数关系、以及织物材料的最优厚度。考虑到本文对传热方式只考虑热传导方式,故引入补偿系数,减小模型的误差。本模型为高温作业专用服装的设计和成本控制提供可靠的依据。本文还可以用于保温玻璃的保温效果预测、建筑物在冬季保温层的隔热效果预测,且本文的精度较高,得到的预测结果比较准确。
关键词 :高温作业专用服装,集总参数法,差分模型,最优化

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 背景知识
1.1. 背景介绍
高温作业专业服装指在高温环境中穿用的、维护穿着者人身安全的防护服。耐高温防护服隔离辐射热,但服装附带的管道限制了穿着者的灵活性。高温作业专业服装正顺应现实的需求而经历着一场科技的革新。在高温作业专业服装领域,国内取得了不错的成绩,但与先进国家仍有相当大的差距;同时部分国家的高温作业专业服装所用的材料大部分都属于高技术纤维,隔热效果更好。随着社会的不断发展,耐高温热防护服的舒适性越来越得到人们的重视 [1]。
在高温作业专用服装的实际应用中,外界热量主要是以热传导、热对流、热辐射三种形式传递,使人皮肤外侧的温度升高。必须具备较好的减缓和阻止热量传递的性能,避免热源对人体造成伤害,为高温环境下作业提供良好的热防护服的隔热性。专用服装通常由三层织物材料构成,记为I、II、III层,其中I层与外界环境接触,III层与皮肤之间还存在空隙,将此空隙记为IV层。
1.2. 研究意义
这种高温作业专用服装不仅可以作为冶金、石油化工和电力等众多行业使用,并能用作宇航服、警用防爆服、消防服。研究设计高温作业专业服装各层材料的厚度,不仅能在性能方面可以有效的减缓或阻止热量传递,避免热源传导热量对人体造成伤害,还可以从经济成本方面,求出性能有效且成本合理的服装设计方式。对我国高温作业行业的发展有重要意义 [2]。
2. 问题的分析
2.1. 对环境温度为75℃、II层厚度为6 mm、IV层厚度为5 mm,研究人皮肤外侧的温度分布
首先根据物理学知识,选取合适的参数,构建合理的数学模型,计算出温度分布。首先根据资料,分析研究各个参数代表的物理意义以及其运用,其次确定传热方式以及相关运算公式,运用双层玻璃的热损耗相同的原理计算相关系数,最后根据已知参数构建合理的数学模型,确定各层温度与时间的函数关系。
2.2. 当环境温度为65℃、IV层的厚度为5.5 mm时,确定II层的最优厚度, 确保工作60分钟时,不超过人体承受范围
首先根据已知参数建立关于质量的目标函数,其次确定约束条件、运用最优化模型,最后使用LINGO软件,得到65℃环境中第II层的最优厚度、各层在65℃环境中第60分钟的温度以及第III层在第55分钟的温度。
2.3. 当环境温度为80℃时,确定II层和IV层的最优厚度,确保工作30分钟时, 假人皮肤外侧温度不超过47℃,且超过44℃的时间不超过5分钟
首先根据参数查阅相关模型资料,其次确定使用差分求解抛物型偏微分方程模型确定各层温度与时间温度的函数关系,运用MATLAB绘制三维立体等温线图像,分别得到第II层和第IV层温度与时间、厚度函数图像,然后在图像上找到满足条件的坐标,从而确定80℃环境中II、IV层的最优厚度。
本文数据来源于2018年全国大学生数学建模竞赛A题,为了便于解决问题,提出以下假设:
1、假设热传导是唯一的传热方式;
2、假设材料的厚度为其特征尺寸;
3、织物材料无褶皱且表面温度处处相等;
4、假设温度传递只存在一维传递且沿着温度梯度方向;
5、假设防护服的表面积与人体的表面积相等,均为1.6 m2;
6、假设材料的热传导率与表面传感系数在数值上相等;
7、假设不存在导热热阻;
8、假设第III、IV层温度为衣服温度 ;第I、II层温度为体内温度 。
3. 模型的建立与求解
3.1. 环境温度75℃时,关于服装温度变化的研究
3.1.1. 研究思路
探究在环境温度为75℃情况下,穿着高温作业专业服装工作在90分钟内的各层温度变化情况。设定第II层厚度为6 mm,第IV层厚度为5 mm。运用双层玻璃的热量损耗相同的原理计算出补偿系数g,最后运用集总参数法预测的温度分布数学模型,并运用MATLAB软件,分析各层织物温度变化 [3]。
3.1.2. 研究方法
模型I——双层玻璃热量流失模型
1) 模型原理
均匀介质的厚度表示为d,两侧流体温度差表示为 ,在单位时间内由温度较高的流体向温度低的流体单位面积传递的热量为Q,与 成正比,与d成反比,即
其中:k——热传导系数。
2) 模型建立
外界环境的温度表示为 ,第I层织物材料温度表示为 ,热传导系数表示为 ,厚度为 ;第II层织物材料温度表示为 ,热传导系数表示为 ,厚度表示为 ;第III层织物材料温度表示为 ,热传导系数表示为 ,厚度表示为 ;第IV层温度表示为 ,热传导系数表示为 ,厚度表示为 。
由上式单位时间单位面积的热量传导(热量流失)模型可列:
其中:Q——单位时间单位面积的热量。
3) 模型数据处理
由附件二数据,第IV层温度在90分钟时 。且环境温度 ,体内温度为 ,第II层厚度 ,第IV层厚度 。将数据带入上式中,可解得: [4]
模型II——利用集总参数法预测的温度分布模型
1) 模型的建立
根据物体非稳态导热的导热微分方程,可列得:
其中:h——表面传热系数;A——传热表面面积;V——体积;c——比热容;
——表示传热物质密度;
①方程的整理:
其中, 为当前织物的外层在75℃时的温度。由于假设温度传递只存在一维传递且沿着温度梯度方向,故引入补偿系数g。
当前织物的外层在75℃时的温度,即每个方程分别用 、 、 代替上式的 ,
将模型一结论 , , 代入方程中,解出补偿系数g。并带入上述方程解得
第I层温度函数 :
第II层温度函数 :
第III层温度函数 :
第IV层温度函数 :
3.2. 环境温度65℃时,第二层最优厚度的研究
3.2.1. 研究思路
首先根据已知参数建立目标函数,其次由已知资料确定约束条件、构建最优化模型,最后利用LINGO软件,确定II层的最优厚度,确保工作60分钟时,不超过人体承受范围;以及第IV层在第60分钟内的温度变化。
3.2.2. 研究方法
模型III——最优化模型
1) 模型准备
确定第II层的最优厚度是能确保工作60分钟时,假人皮肤外侧温度不超过47℃且超过44℃的时间不超过5分钟,即求第II层的最小厚度,可转化为求高温作业专业服装的最小质量。根据已知环境温度65℃,IV层的厚度为5.5 mm,一般高温作业专用服装最大质量不超过12 kg,可以利用最优化模型求解。
根据热力学知识可知,第IV层与人皮肤外侧相接触,可认为第IV层温度为人皮肤外侧温度。可限定第IV层最高温度为47℃,且超过44℃的时间不超过5分钟。
2) 模型的建立
高温作业专用服装质量m,即
服装总质量是各层织物材料质量之和,即
已知第二层厚度 ,即
当前环境温度 ,即
环境温度75℃较65℃热量流失更大,运用研究一的双层玻璃传热模型,可以得到第I层与第II层之间的代数关系。
解不等式得:
即第I层与第II层的最大温差不会超过8.87℃。
由问题研究一解出的第IV层补偿系数即
由双层玻璃热量流失模型得:
在65℃时:
第IV层温度分布模型:
在 时假人皮肤外侧温度不超过44℃
在整个热传递过程中,假人皮肤外侧温度不超过47℃
在时间 时,温度应超过44℃,即
第III层温度应大于47℃,即
3) 模型的求解
得到第II层最小厚度 (图中D2)为8.17 mm。
将 代入问题研究一模型中。在60分钟时,可以确定各层的温度如表1所示。
Table 1. Temperature form of each layer in 60 minutes
表1. 60分钟时各层温度表
可以得出,在 ,即55分钟时的第Ⅳ层温度为43.8℃,在 即60分钟时温度为44.77℃。
3.3. 当环境温度为80℃,确定II层和IV层的最优厚度
3.3.1. 研究思路
利用差分方程模型建立一维热传导方程,求出各层织物材料的温度分布,达到确保工作30分钟后,人皮肤外侧温度不超过47℃情况下的最小厚度,即可确定第II层和第IV层的最优厚度。
3.3.2. 研究方法
模型IV——差分方程模型
1) 模型原理与建立
由资料可知,高温作业专业服装共分为4层,记为I、II、III、IV。环境的温度是恒定的为80℃,假人体内温度的是恒定的37℃,高温作业服每层织物材料热传导率分别为 ,本文要分析在高温环境即80℃工作时,热量传导至假人皮肤外侧的规律,以及高温作业装各层织物材料的温度分布,进而确定第II层和第IV层的最优厚度。
服装各层织物材料可以建立一维热传导方程为
其中: ——第i高温防护服各层织物材料的温度分布; ——为各层织物材料的热传导系数; ——比热容; ——各层物质密度;l——服装上一点至最外侧得距离;
以上皆为题目已知的常数,且 [5]。
由假设可知,各层织物材料之间在热传导界面处热传导率保持平衡状态,且温度相等,即
根据上式分析,建立的高温作业服热传导微分方程模型为
2) 模型求解
根据上述差分方程模型,利用MATLAB软件进行求解,绘制图像:
其中:图像将时间变量x单位设置为 ;
x——时间;d(Y)——厚度(空间变量);U——温度;
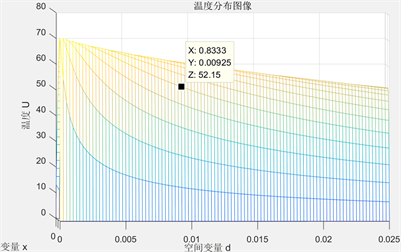
Figure 1. The II layer relationship of temperature distribution to thickness
图1. 第II层温度分布与厚度d (空间变量)关系
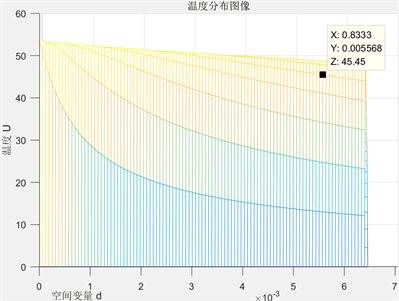
Figure 2. The IV layer relationship of temperature distribution to thickness
图2. 第IV层温度分布与厚度d空间变量关系
见图1、图2,根据温度分布与厚度d关系,当温度恒定时,第II层织物材料和第IV层越厚,温度越低,其延缓热量传递和隔绝热量的能力更强,表示高温防护服的隔热性能更好。
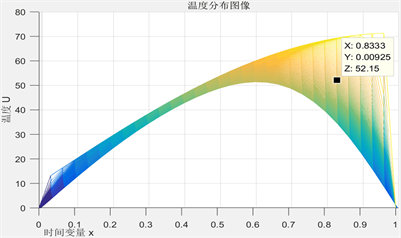
Figure 3. The II layer relationship of temperature distribution to time variable
图3. 第II层温度分布与时间变量关系图
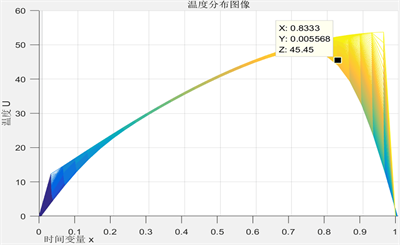
Figure 4. The IV layer relationship of temperature distribution to time variable
图4. 第IV层温度分布与时间变量关系
见图3、图4,根据温度分布与时间变量x的关系,当厚度恒定时,第II层和第IV层在高温环境下受到热源传导热量的时间越长,其能达到的温度越高,但随时间增大,温差减小,温度升高的趋势减缓。
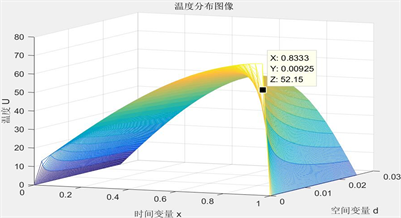
Figure 5. The II layer relationship of temperature distribution, time variable and thickness
图5. 第II层温度分布、时间、空间变量关系
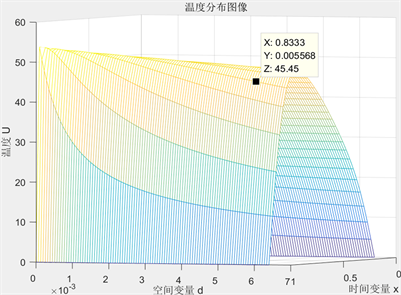
Figure 6. The IV layer relationship of temperature distribution, time variable and thickness
图6. 第IV层温度分布、时间、空间变量关系
见图5、图6。呈现温度分布、时间、空间变量三者的关系,可以据图选出最优厚度:
根据研究三中,设定工作30分钟时,假人皮肤外侧温度不超过47℃,超过44℃不超过5分钟,可认为在时间在25分钟时,即图像中 时温度第IV层温度不超过44℃。既可以认为在此时的厚度为最优厚度。即求得第II层织物材料最优厚度 ,此时温度为52.15℃;即第IV层织物材料最优厚度求得 ,此时温度为45.45℃。
4. 结论
针对研究一,在已知条件下,建立数学模型,计算温度分布。对数据进行分析,并应用集总参数法,构建了服装各层材料温度分布模型(微分方程)。运用双层玻璃传热模型计算出各层材料的边界温度值。运用MATLAB软件编程求解上述带边界条件的微分方程模型。得出每层织物材料和空隙Ⅳ层的温度分布情况:即,先升温较快,到达一定温度后,缓慢升温。
针对研究二,要求在环境温度为65℃,计算第II层最优厚度。本文以专用服装的质量为目标函数,建立了其与服装各层材料的厚度和密度之间的关系模型。运用双层玻璃传热模型,计算出每一层的边界温度值,确定出第I层与第II层之间最大温差。将此温差作为优化问题的一个约束条件。再根据研究一中的模型确定其它约束条件。最后应用LINGO软件求解上述约束优化问题,计算出服装最优质量,从而得到II层材料的最优厚度。
针对研究三,要求在环境温度为80℃,确定第II、IV层的最优厚度。对永冻土层热传导模型改进,构建出反应温度和时间关系的差分方程模型。利用MATLAB对模型进行求解并绘制反应温度、时间、厚度关系的三维图像。将温度、时间、厚度其中之一作为常量,又得到了它们两两之间的关系图像。总结分析出满足题设条件下,II、IV层的最优厚度。
本文中的模型的精度较高,预测结果比较准确,可以广泛运用于多层材料热传导的方式研究。
文章引用
王玉婷,秦浩然,张广浩,张凯森. 高温作业专用服装的研究
The Research of Special Clothing for High Temperature Operation[J]. 应用数学进展, 2018, 07(12): 1583-1592. https://doi.org/10.12677/AAM.2018.712185
参考文献
- 1. 华涛. 热防护服热防护性能的分析与探讨[J]. 产业用纺织品, 2002(8): 28-31.
- 2. 李俊, 等. 耐高温防护服及其发展趋势[EB/OL]. 百度文库. https://wenku.baidu.com/view/5214ac6a2f3f5727a5e9856a561252d380eb2018.html?tdsourcetag=s_pctim_aiomsg&qq-pf-to=pcqq.group
- 3. 戴锅生. 传热学[M]. 第2版. 北京: 高等教育出版社, 1999.
- 4. 李庆杨, 王能超, 易大义. 数值分析[M]. 第5版. 北京: 清华大学出版社, 2008.
- 5. 百度文库. 永冻土层热传导问题数学建模[EB/OL]. https://wenku.baidu.com/view/4cdf33421a37f111f0855bab.html
