Advances in Applied Mathematics
Vol.
08
No.
02
(
2019
), Article ID:
28972
,
9
pages
10.12677/AAM.2019.82033
Stochastic Stability of a Class of Neutral Markovian Jumping Systems
Bang Luo, Changchun Shen, Juan Li, Shouwei Zhou
School of Data Science and Information Engineering, Guizhou Minzu University, Guiyang Guizhou
Email: lb_waclj@126.com
Received: Jan. 30th, 2019; accepted: Feb. 14th, 2019; published: Feb. 22nd, 2019

ABSTRACT
Stability is one of the most important properties of dynamical system, which has important theoretical significance to solve practical problems. The existence of time-delays is the root of system performance difference and systematic instability, so it has been considered by many scientists and scholars at home and abroad. In this paper, the stochastic stability of a class of neutral Markovian jumping systems is considered. Firstly, the Lyapunov function is constructed, and the sufficient conditions of stochastic stability are obtained by using Jensen's inequality. Secondly, the LMI toolbox in Matlab is used to verify the correctness of the results. Finally, two examples are given to verify the validity of this method.
Keywords:Neutral System, Markovian Jumping Systems, Stochastic Stability, Jensen’s Inequality
一类中立型马尔科夫跳跃系统的随机稳定性
罗邦,沈长春,李娟,周守维
贵州民族大学,数据科学与信息工程学院,贵州 贵阳
Email: lb_waclj@126.com
收稿日期:2019年1月30日;录用日期:2019年2月14日;发布日期:2019年2月22日
摘 要
稳定性是动力系统最重要的性质之一,对解决实际问题具有很重要的理论意义。而时滞的存在是系统性能变差和系统不稳定的根源,故国内外许多专家和学者对其进行研究。本文考虑了一类中立型马尔科夫跳跃系统的随机稳定性问题。首先,通过构造lyapunov函数,利用Ito’s引理和Jensen’s不等式,获得随机稳定性的充分条件。其次,使用matlab中的LMI工具箱,验证结果的正确性。最后,给出两个实例,验证此方法的有效性。
关键词 :中立型系统,马尔科夫跳跃系统,随机稳定性,Jensen’s不等式
Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
17世纪初,Newton和Leibniz发明了微积分,同时也开创了微分方程的研究。1771年,Condorcet导出历史上第一个时滞微分方程,时滞微分方程就是时间滞后的微分方程,用于描述即依赖当前状态也依赖过去状态的微分方程。时滞微分方程所构建的时滞微分系统在现实世界中有着广泛的应用:经济系统、机械系统、计算机网络系统、制造系统等 [1] 。中立型时滞系统的研究起步较早,并且取得非常丰硕的研究成果。中立型时滞系统是存在于客观世界中的一种典型系统,时滞的存在是系统不稳定和性能变差的主要原因之一。因此,研究中立型时滞系统的稳定性是非常有必要的 [2] [3] 。文献 [4] 考虑用多积分的方法对中立型时滞系统进行研究,并且取得很好的结果。文献 [5] 中沈博士分别从“离散时变时滞”、“分布式时变时滞”、“非线性扰动和不确定时变时滞”和“离散延迟随时间变化”等几个方面对中立型时滞系统的稳定性进行深入考虑,并且取得了很好的结果。
中立型马尔科夫跳跃系统是一类特殊的中立型时滞微分系统,系统的转移概率由马尔科夫过程控制。由于此类系统能更好地描述且解决实际问题,故引起国内外很多专家和学者进行研究,并且取得了很丰硕的结果 [6] - [12] 。
本文考虑了一类中立型马尔可夫跳跃系统的随机稳定性问题。通过构造lyapunov函数,利用Jensen’s不等式对系统进行分析,获得满足随机稳定性的充分条件。
2. 系统描述
首先,考虑以下具有离散时滞和时变时滞的中立型马尔科夫跳跃系统
(1)
其中,
是状态向量,
,
是离散时滞,
是时变时滞。
且满足以下不等式
(2)
是已知常数矩阵,
在有限状态概率空间
中取值,
,具有以下性质
(3)
其中,
,对任意的
,
表示由t时刻的第i状态转移到
时刻的第j状态的概率,并且有
,状态转移概率矩阵为
(4)
其中
表示未知的状态转移概率,对于任意的
,集合
表示
,其中
此外,
是一个非空集,可以表示为
,其中
为非负整数,
表示在状态转移概率矩阵
中第i行第j列的已知元素。
3. 引理及结论
定义1 [13] :对于系统(1),若
时满足以下条件
(5)
则系统是随机稳定的。
引理1 [14] :(Ito’s lemma)若
,Lyapunov函数满足以下等式
(6)
则系统是稳定的。
引理2 [15] :(Jensen’s inequality)假设
和
,对于任意正定矩阵W有以下不等式成立
(7)
引理3 [16] :对于任意正定矩阵
,标量
,向量函数
可积时有以下不等式成立
(8)
为方便起见,有以下代替
定理1:若存在实对称矩阵
,适当维数的实矩阵
且
,则系统(1)是随机稳定的。
(9)
其中
证明:构造lyapunov函数
(10)
其中
由引理1可得
(11)
(12)
由引理2:(Jensen’s inequality),可得
(13)
由
可得
(14)
(15)
(16)
由(14)~(16)式,有以下不等式成立
(17)
(18)
从系统(1)可知
(19)
其中
综合(11)~(13)和(17)~(19)式,可得
其中
可得稳定性的充分条件
,即
(20)
证明系统(1)是随机稳定的。
其次,考虑以下具有时变时滞和分布时滞的中立型马尔科夫跳跃系统
(21)
推论1:若存在实对称矩阵
,适当维数的实矩阵
且
,则系统(21)是随机稳定的。
(22)
其中
证明:推论1的证明过程和定理1类似,但需要构造如下的lyapunov函数
由引理3得
(23)
同理,由系统(21)可得
(24)
其中
综合(11)~(13)、(17)~(19)、(23)和(24)式,得证推论1。
4. 数值仿真
在这一部分,我们给出两个仿真算例,来验证理论结果的有效性。
例1:考虑以下具有离散时滞和时变时滞的中立型马尔科夫跳跃系统
在这里,我们的目的是使用matlab中的LMI工具箱验证定理1中结果的有效性,假设初始状态
,可得系统的状态轨迹图(见图1,具有离散时滞和时变时滞的中立型马尔科夫跳跃系统状态轨迹图)。
例2:考虑以下具有时变时滞和分布时滞的中立型马尔科夫跳跃系统

Figure 1. The state trajectories of a neutral Markov jumping system with discrete and time-varying delays
图1. 具有离散时滞和时变时滞的中立型马尔科夫跳跃系统状态轨迹图
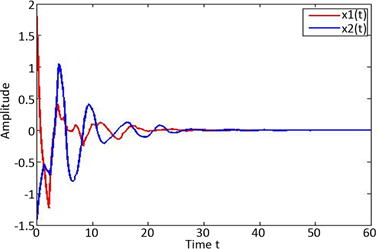
Figure 2. The state trajectory of a neutral Markov jumping system with time-varying delay and distributed delay
图2. 具有时变时滞和分布时滞的中立型马尔科夫跳跃系统状态轨迹图
在这里,我们的目的是使用matlab中的LMI工具箱验证推论1中结果的有效性,假设初始状态
,可得系统的状态轨迹图(见图2,具有时变时滞和分布时滞的中立型马尔科夫跳跃系统状态轨迹图)。
5. 结论
本文考虑了一类中立型马尔可夫跳跃系统的随机稳定性问题。首先,通过构造lyapunov函数,利用Ito’s引理和Jensen’s不等式获得随机稳定性的充分条件。其次,使用matlab LMI工具箱验证结果的正确性。最后,列举两个实例,对此方法的有效性进行验证。
基金项目
贵州省科技厅科学研究基金(J[2015]2074),贵州省科技厅、贵州民族大学联合基金项目(LKM[2013]21),贵州省教育厅群体创新研究项目贵州民族大学博士启动基金项目(KY[2016]021),贵州民族大学科研基金资助项目(2017YB066)。
文章引用
罗 邦,沈长春,李 娟,周守维. 一类中立型马尔科夫跳跃系统的随机稳定性
Stochastic Stability of a Class of Neutral Markovian Jumping Systems[J]. 应用数学进展, 2019, 08(02): 292-300. https://doi.org/10.12677/AAM.2019.82033
参考文献
- 1. 李文林. 数学史教程[M]. 北京: 高等教育出版社, 2002: 1-7.
- 2. 黄在堂. 时滞随机微分系统的动力学性质研究[D]: [博士学位论文]. 广东: 华南理工大学, 2011.
- 3. 孙乐平. 中立型方程的稳定性:边界准则[J]. 上海师范大学学报(自然科学版), 2001, 30(4): 34-39.
- 4. Fang, M. and Park, J.H. (2013) A Multiple Integral Approach to Sta-bility of Neutral Time-Delay Systems. Applied Mathematics Computation, 224, 714-718. https://doi.org/10.1016/j.amc.2013.08.078
- 5. 沈长春. 中立型系统的稳定性与可达集边界[M]. 成都: 西南交通大学出版社, 2015: 1-208.
- 6. Borno, I. and Gajic, Z. (1995) Parallel Algorithm for Solving Coupled Algebraic Lyapunov Equations of Discrete-Time Jump Linear Systems. Computers Mathematics with Applications, 30, 1-4.
https://doi.org/10.1016/0898-1221(95)00119-J
- 7. Zhang, J., Han, Z. and Zhu, F. (2014) Stochastic Stability and Stabilization of Positive Systems with Markovian Jump Parameters. Nonlinear Analysis: Hybrid Systems, 12, 147-155. https://doi.org/10.1016/j.nahs.2013.12.002
- 8. Han, W., Liu, Y. and Wang, L. (2010) Robust Exponential Sta-bility of Markovian Jumping Neural Networks with Mode-Dependent Delay. Communications in Nonlinear Science and Numerical Simulation, 15, 2529-2535.
https://doi.org/10.1016/j.cnsns.2009.09.024
- 9. 张维海, 刘鹤鸣. 随机马尔科夫跳跃系统有限时间控制[J]. 控制理论与应用, 2015, 32(3): 334-340.
- 10. 高丽君. 具有Markov切换的跳跃系统稳定性分析[D]: [博士学位论文]. 山东: 曲阜师范大学, 2007.
- 11. 陈凌婕. 两类含有时变转移概率的Markov跳跃系统的研究[D]: [博士学位论文]. 黑龙江: 哈尔滨工业大学, 2011.
- 12. Xiong, L.L., Zhang, H.Y. and Liu, Z.X. (2016) Improved Stability and Math Container Loading Mathjax Performance for Neutral Systems with Uncertain Markovian Jump. Nonlinear Analysis Hybrid Systems, 19, 13-25.
https://doi.org/10.1016/j.nahs.2015.07.005
- 13. Ma, Q., Xu, S.Y. and Zou, Y. (2011) Stability and Synchroniza-tion for Markovian Jump Neural Networks with Partly Unknown Transition Probabilities. Neurocomputing, 74, 3404-3411. https://doi.org/10.1016/j.neucom.2011.05.018
- 14. Zou, Z. and Wang, Y. (2006) New Stability Crite-rion for a Class of Linear Systems with Time-Varying Delay and Nonlinear Perturbations. IEE Proceedings Control Theory and Applications, 153, 623-626.
https://doi.org/10.1049/ip-cta:20045258
- 15. Han, Q.L. (2004) On Robust Stability for a Class of Linear Sys-tems with Time_Delay and Nonlinear Perturbations. Appera in Computers and Mathematics with Applications, 23, 235-241.
- 16. Beyd, S., Ei, L., Ghaoui, I., Feron, E. and Balakrishnan, V. (1994) Linear Matrix Lnequalities in Systems and Control Theory. Studies in Applied Mathematics, 105, 76-82.




