Advances in Applied Mathematics
Vol.
08
No.
06
(
2019
), Article ID:
31059
,
6
pages
10.12677/AAM.2019.86134
On the Extremal Wiener Indices of Graphs with Given Clique Number
Yuanlong Chen, Xiaoying Wu*
School of Financial Mathematics and Statistics, Guangdong University of Finance, Guangzhou Guangdong
Received: Jun. 11th, 2019; accepted: Jun. 21st, 2019; published: Jun. 28th, 2019

ABSTRACT
In this paper, we investigate the Wiener index for connected graphs of given clique number, obtain sharp lower and upper bounds on Wiener index for connected graphs of order n with clique number l. For connected graphs of order n with clique number l, by the method of shift-joint deformation, we obtain the largest Wiener index graph and the smallest Wiener index graph are and Tuŕan graph, respectively.
Keywords:Graph, Wiener Index, Extremal Graphs, Clique Number
给定团数的Wiener指数极图
陈员龙,吴小英*
广东金融学院金融数学与统计学院,广东 广州
收稿日期:2019年6月11日;录用日期:2019年6月21日;发布日期:2019年6月28日

摘 要
本文研究一类给定团数的连通图的Wiener指数,讨论和刻画了团数为l的n阶连通图的Wiener指数的上界和下界,通过移接变形等方法证明了团数为l的n阶连通图中具有最大,最小Wiener指数的极值图分别为 与Tuŕan图。
关键词 :图,Wiener指数,极图,团数

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
分子拓扑学是一门应用于图论、化学、拓扑学等相互交叉的学科,是当前的一个热门研究领域。分分子拓扑学的一个最重要研究方向是分子拓扑指数,其中关于拓扑指数的极值研究为计算机搜索算法确定分子图的顶点数与边数的上下确界范围提供理论依据,从而提高计算机的搜索算法的效率。因而关于分子拓扑指数的最大或最小拓扑指数图的研究成为化学分子图的研究热点,近年来许多研究者对其进行深入研究并取得很多有意义的结果 [1] - [9] [11] [12] [13] 。
Wiener指数可以用来解释烷烃的物理化学性质的变化,分子结构与药理性能的关系,因此确定Wiener指数的极值图对分子化学应用有着非常重要的意义。早在上个世纪70年代Entringer等在 [10] 中证明了n阶树中具有最大、最小Wiener指数的极值图分别是路 与星图 。随后出现许多关于Wiener指数的数学与化学的结论,特别是树的Wiener指数研究。例如Jelena等在 [14] 中讨论了给定最大度的n阶树,获得此类树的最小Wiener指数极值图。刘慧清等在 [3] [4] 中分别讨论了给定直径的n阶树的最小Wiener指数极值图与及给定r个圈的n阶连通图的四类拓扑指数极值图。王华在研究给定度序列的n阶树时 [15] ,确定了最大与最小的Wiener指数极值图。Dobrynin等在 [13] 中对近年关树的Wiener指数的重要研究结果做了一个综述,并给出了几个猜想及公开问题。
本文考虑了给定团数的n阶连通图的Wiener指数的值图。通过移接变形等方法证明了团数为l的n阶连通图中具有最大,最小Wiener指数的极值图分别为 与Tuŕan图。
2. 基本引理
在这一节我们先给出一些相关引理。设 是一个 阶团, 。设 , 是一个n阶简单连通图,它是在团 的每个顶点 上分别附上阶为 的树 得到的图, 是一个n阶简单连通图,它是在团 的每个顶点 上分别附上阶为 的路 得到的图,其中 。记
引理1 [2] 设G是一个连通图, , 是G的两个连通子图并且有唯一的公共点u, 。设 , 。那么 。
引理2设 , 分别是阶为n的树和路。 是 中最长的一条路。如果 且 , 且 ,那么 且等号成立当且仅当 。
证明: ,
,
我们有 ,因此 且等号成立当且仅当 。
设图 , 是两个连通图且 。 是一个连通图且
, , 。
引理3 [13] 设 分别是阶为n的树和路,那么 且等号成立当且仅当 。
引理4 设H是阶为 的连通图, 是一棵阶为 的树, 是一条阶为 的路且 , ,则 且等号成立当且仅当 。
证明:由引理1有 ,根据引理2,3有 ,因此 且等号成立当且仅当 。
由Wiener指数的定义我们有
引理5 设G是一个简单连通图且
。如果边
,那么 。
。
由引理5我们有
引理6 设 且 ,如果 ,那么 且 ,其中 表示添加一条连接图G中不相邻的两点 的边得到的图。
引理7 设 , 分别是阶为 的两条不同的路。
(见图1)。则 。
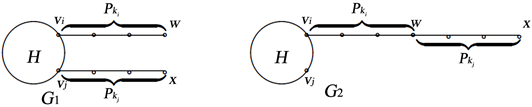
Figure 1. Two graphs
图1. 两种图例
证明:由引理1我们有
,
。
直接计算有
因为 ,所以 。因此 ,也即 。又因为 , ,所以
故 。
3. 项给定团数的图的Wiener指数极图
定理 1设 ,那么 且等号成立当且仅当 。
证明:我们选择 使得 尽可能大。
断言1 如果 是具有最大Wiener指数的图,那么 。
断言1的证明:否则,我们假设 ,那么存在一个圈 且有 ,但 。设 为图G删除边xy那么 。由引理6有。这与G的选择矛盾,所以断言1成立。
断言2 如果 是具有最大Wiener指数的图,那么 。
断言2的证明:由断言1有 。由引理4有 。所以断言2成立。
断言3 如果 是具有最大Wiener指数的图,那么 。
断言3的证明:否则,我们假设G不同构 。由断言2有 。设 , 。那么G至少有两条阶大于1的路 附在团 的两个不同的顶点 上。令 , ,由引
理7有 。这与G的选择矛盾,因此我们有 。
综上所述知定理成立。
定理2 如果 是具有最小Wiener指数的图,那么G是Tuŕan图。
证明:我们选择 使得 尽可能小。由G的团数为l,因而G中至少有一个团 ,
不妨设为 , 。设 。下面我们先证明三个断言:
断言1 在G中, 中每个点至多与 中 个顶点都相邻。
断言1的证明:否则,G中有完全图 ,与G的团数为 矛盾,所以断言1成立。
断言2 如果 ,则 是一个完全图 。
断言2的证明:否则,设 中最大完全图为 。由断言1知 中每个顶点与 中至少一个顶点距离大于等2。设 ,由 为 中最大完全图,所以 中每个点至多与 中 个点都相邻(否则, 中有更大的完全图,矛盾),也即 中每个顶点与 中至少一个顶
点距离大于等于2。因此我们有
,
这与G的选择矛盾,所以断言2成立。
断言3 如果 ,则 中含阶数最大为l的完全图 。
断言3的证明:否则,如果 中不含完全图 ,设 中最大完全图为 ,设 , 中最大完全图为 ,依此类推,设 , 中最大完全图为 。由断言1知 中每个顶点与 中至少一个顶点的距离大于等于2,由 为 中最大完全图,所以 中每个顶点至多与 中 个点都相邻,也即 中每个顶点与 中至少一个顶点的距离大于等于2。依此类推,由 为 中最大完全图,所以 中每个顶点至多与 中 个顶点都相邻,也即 中每个顶点与 中至少一个顶点的距离大于等于2,其中 。因此我们有
这与G的选择矛盾,以 中有完全图 。又因为G的团数为l,所以 中含有阶数最大为l的完全图。所以断言3成立。
设 ,则 。由断言3可知G中有t个顶点互不相交的l团,不妨设为 , , ,…,
。
根据断言2可知G中有一个与这t个l团顶点都不相交的r团 。
设 。下面说明这些团之间哪些顶点相邻。
(i) 对前t个l团中任意两个l团必有其中一个团的每个顶点正好与另一个团的 个顶点都相邻.根据G的团数为l,则其中任意一个团的每个顶点至多与另一个团的 个顶点都相邻。否则,G中存在阶数为 的团,这与G的团数为l矛盾。根据 尽可能小及断言3中类似分析可知,其中任意一个团的每个顶点正好与另一个团的 个顶点都相邻。
下面证明t个l团之间哪些顶点相邻。
首先我们考虑
,
之间哪些顶点相邻。由1)知
中每个顶点与
中
个顶点都相邻,对于
不失一般性可设
,
。对于
,必定有
。否则,
与
中至多
个顶点相邻。与(i)矛盾。又因为
与
中
个顶点相邻,即
与 中一个顶点不相邻,不妨设为
,即
。从而
。类似讨论可设
,
。重复上面的讨论,可得
。我们断言对任意
有
。否则,因为
与
构成一个l团,
与
构成一个l团,所以
,
与
构成一个
团。与G的团数为l矛盾。同理可得
。
中一个顶点不相邻,不妨设为
,即
。从而
。类似讨论可设
,
。重复上面的讨论,可得
。我们断言对任意
有
。否则,因为
与
构成一个l团,
与
构成一个l团,所以
,
与
构成一个
团。与G的团数为l矛盾。同理可得
。
重复上面的讨论,我们对这t个顶点互不相交的l团可设
(ii) 类似上面的讨论,可知第 个r团 中每个顶点正好与前t个顶点互不相交的l团
的 个顶点都相邻。不失一般性可设
综上可知 构成r个顶点数为 的空图 ,
构成 个顶点数为t的空图 。
因此图G是一个Tuŕan图 。
基金项目
本文工作受到广东省自然科学基金(2017A030313037)和广东金融学院2017创新强校工程项目(20170406101, 20170502151)资助。
文章引用
陈员龙,吴小英. 给定团数的Wiener指数极图
On the Extremal Wiener Indices of Graphs with Given Clique Number[J]. 应用数学进展, 2019, 08(06): 1160-1165. https://doi.org/10.12677/AAM.2019.86134
参考文献
- 1. Entringer, R. and Jackson, D. (1976) Snyder D Distance in Graphs. Czechoslovak Mathematical Journal, 26, 283-296.
- 2. You, Z.-F., Huang, Y. and Du, X. (2018) A Note on Comparison between the Wiener Index and the Za-greb Indices. Communications in Mathematical Research, 34, 296-302.
- 3. Das, K.C. and Nadjafi-Arani, M.J. (2017) On Maximum Wiener Index of Trees and Graphs with Given Radius. Journal of Combinatorial Optimization, 34, 574-587. https://doi.org/10.1007/s10878-016-0092-y
- 4. Gutman, I. and Yeh, Y.N. (1995) The Sum of All Dis-tances in Bipartite Graphs. Mathematica Slovaca, 45, 327-334.
- 5. Berega, S. and Wang, H. (2007) Wiener Indices of Balanced Binary Trees. Discrete Applied Mathematics, 155, 457-467. https://doi.org/10.1016/j.dam.2006.08.003
- 6. Czabarkaě, E., Szěkely, L. and Wagner, S. (2009) The Inverse Problem for Certain Tree Parameters. Discrete Applied Mathematics, 157, 3314-3319. https://doi.org/10.1016/j.dam.2009.07.004
- 7. Li, X.L. and Wang, L. (2004) Solutions for Two Conjectures on the Inverse Problem of the Wiener Index of Peptoids. SIAM Journal on Discrete Mathematics, 17, 210-218. https://doi.org/10.1137/S0895480101387261
- 8. Wu, X.Y. and Liu, H.Q. (2010) On the Wiener Index of Graphs. Acta Applicandae Mathematicae, 110, 535-544. https://doi.org/10.1007/s10440-009-9460-2
- 9. Liu, H.Q. and Pan, X.F. (2008) Minimal Wiener Index of Trees with Fixed Diameter. MATCH Communications in Mathematical and in Computer Chemistry, 60, 85-94.
- 10. Dimitrov, D., Ikica, B. and Škrekovski, R. (2019) Maximum External Wiener Index of Graphs. Discrete Applied Mathematics, 257, 331-337. https://doi.org/10.1016/j.dam.2018.09.024
- 11. Lepovic, M. and Gutman, I. (1998) A Collective Property of Trees and Chemical Trees. Journal of Chemical Information and Modeling, 38, 823-826. https://doi.org/10.1021/ci980004b
- 12. Goldman, D., Istrail, S., Lancia, G., Piccolboni, A. and Walenz, B. (2000) Algorithmic Strategies in Combinatorial Chemistry. In: Proceedings of the 11th Annual ACM-SIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics, Philadelphia, PA, 275-284.
- 13. Wagner, S. (2006) A Class of Trees and Its Wiener Index. Acta Applicandae Mathematicae, 91, 119-132. https://doi.org/10.1007/s10440-006-9026-5
- 14. Ban, Y.-E.A., Bespamyatnikh, S. and Mustafa, N.H. (2004) A Conjecture on Wiener Indices in Combinatorial Chemistry. Algorithmica, 40, 99-117. https://doi.org/10.1007/s00453-004-1097-y
- 15. Wang, H. (2008) The Extremal Values of the Wiener Index of a Tree with Given Degree Sequence. Discrete Applied Mathematics, 156, 2647-2654. https://doi.org/10.1016/j.dam.2007.11.005
NOTES
*通讯作者。