Advances in Applied Mathematics
Vol.
09
No.
05
(
2020
), Article ID:
35675
,
5
pages
10.12677/AAM.2020.95086
Transformation of Multiple Integral and Its Application in Integral Calculation
Jiaojiao Wang, Guangfeng Chen*, Xintong Wang
Mathematics Department of School of Information Engineering, Xi’an University, Xi’an Shaanxi

Received: May 1st, 2020; accepted: May 14th, 2020; published: May 21st, 2020

ABSTRACT
Multiple integral plays an important role in Higher Mathematics and has an important application in engineering technology. On the basis of the transformation methods of double integral and triple integral variable, this paper discusses the transformation methods of double integral when the region is surrounded by two families of curves and triple integral when the region is surrounded by three families of surfaces, etc., and all kinds of variable transformation method is applied to solve Postgraduate entrance examination questions.
Keywords:Double Integral, Triple Integrals, Variable Transformation, Integral Calculation

重积分的变量变换及其在积分计算中的应用
王娇娇,陈广锋*,王歆彤
西安文理学院信息工程学院数学系,陕西 西安

收稿日期:2020年5月1日;录用日期:2020年5月14日;发布日期:2020年5月21日

摘 要
重积分在高等数学中占有重要的地位,在工程技术中有着重要的应用。本文在二重积分和三重积分变量变换方法的基础之上,讨论了区域由两族曲线围成时二重积分的变换方法及区域由三族曲面围成时三重积分的变换方法等,并将此类方法应用于解决考研中复杂的重积分计算问题。
关键词 :二重积分,三重积分,变量变换,积分计算

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
重积分是微积分学中的一个重要内容,在实际中有着非常重要的应用,因此重积分的计算至关重要。由于重积分在计算时,可能会有多种解法,而有的重积分在用一般的解题方法时很困难,因此需要通过重积分的变量变换来解决积分计算中所遇到的问题,利用简单而又方便的变量变换的方法来解决复杂的重积分计算问题,能为重积分的应用带来更多的便利。
变量变换方法的重点就在于分析被积函数和积分区域的特点,选择合适的变换方法,从而达到可以简便计算的目的,重积分常见的坐标变换有二重积分的极坐标变换,三重积分的柱坐标变换和球坐标变换。本文将在已有变换方法的基础上探寻不同的变量变换方法,使得积分计算具有简便性。
2. 重积分的变量变换
2.1. n重积分的变量变换公式
在有界闭区域V上是可积函数,设变换
将n维 空间中的区域 一一对应地映在 空间上,并形成区域V,函数 分别有连续的一阶偏导数且它函数行列式
则
上式为一般的n重积分的变量变换公式 [1],实际中常常遇到的是 时二重积分以及 时三重积分的计算与应用,文献 [2] [3] [4] [5] [6] 对常见的换元积分法做了讨论及推广,下面着重探讨两种特殊区域的二重积分和三重积分的变量变换公式。
2.2. 积分区域由两族曲线围成的二重积分变量变换公式
如果积分区域D由两族光滑的曲线
中分别取了两条曲线
。
所围成,且 在D上连续,作变量变换
,则
在D上连续,作变量变换
,则
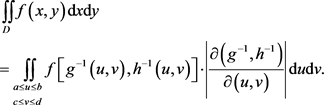
其中 为 的反函数组, 。
2.3. 积分区域由三族曲面围成时的三重积分变量变换公式
如果空间区域V由三族光滑的曲面中分别取了两条曲面 , , ; , , ; , , 所围成,且 在V上连续,作变量变换
则
其中
为
的反函数组,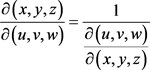 。
。
3. 变量变换在重积分计算问题中的应用
例1:计算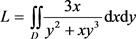 ,其中D为平面曲线
所围成的有界闭区域。(武汉大学)
,其中D为平面曲线
所围成的有界闭区域。(武汉大学)
分析:作积分区域D,如下:
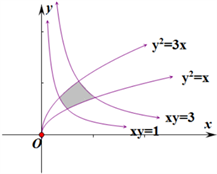
积分区域的边界线方程为 , ,作变换 ,使得积分限容易确定。
解:作变换 ,则积分区域D变为
例2:计算下面曲面所围成的图形的体积: , 。(吉林工业大学)
分析:求体积即求被积函数为1的三重积分,积分区域由三族光滑的曲面 , , ,分别取了两个曲面,也就是当 a = 1,2,b = ±1,c = ±1 时,所以可以利用曲面函数作相应的变换。
解:作变换,
则积分区域V变为
则
4. 结语
本文通过常用的重积分的变量变换公式给出了一种由几族曲线(面)围成的积分区域的变量变换方法,并利用该变量变换方法解决了实际的重积分计算问题。
基金项目
陕西省教育科学规划课题(SGH17H243)。
文章引用
王娇娇,陈广锋,王歆彤. 重积分的变量变换及其在积分计算中的应用
Transformation of Multiple Integral and Its Application in Integral Calculation[J]. 应用数学进展, 2020, 09(05): 728-732. https://doi.org/10.12677/AAM.2020.95086
参考文献
- 1. 华东师范大学数学系. 数学分析: 下册[M]. 第3版. 北京: 高等教育出版社, 2001: 179-195.
- 2. 裴礼文. 数学分析中的典型问题与方法[M]. 北京: 高等教育出版社, 2013.
- 3. 陆宜清. 浅谈重积分的换元积分法[J]. 南阳师范学院学报, 2015,14(6): 46-49.
- 4. 张新燕. 二重积分的几种计算方法[J]. 数学学习与研究(教研版), 2009(6): 80.
- 5. 王俊青. 二重积分的几种换元法[J]. 德州师专学报, 1994(2): 33-38.
- 6. 宋勇. 三重积分计算中变量变换的应用[J]. 内蒙古电大学刊, 2007(3): 113.