Pure Mathematics
Vol.07 No.04(2017), Article ID:21403,12
pages
10.12677/PM.2017.74042
Homotopy Analysis Sumudu Transform Method for Solving a Class of Time Fractional Partial Differential Equations
Bohui Yang, Xindong Zhang*
College of Mathematics Sciences, Xinjiang Normal University, Urumqi Xinjiang

Received: Jun. 29th, 2017; accepted: Jul. 14th, 2017; published: Jul. 19th, 2017

ABSTRACT
In this article we have applied homotopy analysis Sumudu transform method (HASTM) to solve a class of time Fractional partial differential equations (ACFPDEs) with time fractional derivative in Caputo sense. Finally, the accuracy and simplicity of the method are illustrated by the calculation of specific examples.
Keywords:Time Fractional Partial Differential Equation, Sumudu Transform, Homotopy Analysis
一类时间分数阶偏微分方程的同伦分析Sumudu变换解法
杨博慧,张新东*
新疆师范大学 数学科学学院,新疆 乌鲁木齐

收稿日期:2017年6月29日;录用日期:2017年7月14日;发布日期:2017年7月19日

摘 要
本文主要研究同伦分析Sumudu变换方法在求解一类Caputo时间分数阶偏微分方程中的应用。数值算例表明该方法具有较好的准确性和简便性。
关键词 :时间分数阶偏微分方程,Sumudu变换,同伦分析

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
为了把复杂的线性和非线性的分数阶偏微分方程转变为简单的代数形式,许多的分数阶积分和微分变换已经被用来获得FPDE的精确解和近似解 [1] 。Kumar和他的同事们成功地将同伦分析变换方法也就是拉普拉斯变换和同伦分析方法应用于解决分数阶Fornberg-Whitham方程,Volterra积分方程,分数阶波动方程,浅水波传播过程中产生耦合的Boussinesq-Burger方程。Watugala介绍了Sumudu变换并且和Weerakoon讨论了该变换的一些性质 [2] 。此外,Belgacem [3] [4] [5] 提供了Sumudu变换的精确定义,并讨论了应用许多结果、性质和关系求解FDEs和FPDEs的更好的实现方法,从而增加了关于这个变换的文献。一般可以很容易地将许多时间分数阶线性和非线性偏微分方程进行转化,类似的,可以将Caputo,Riemann-Liouville,Ritzs等类型的空间分数阶导数进行转化。文献 [6] 中介绍了求解非线性Riccati微分方程的多级同伦分析方法。目前同伦分析方法被广泛地应用于求解各种类型的线性和非线性偏微分方程 [7] [8] [9] 。
构造偏微分方程的精确解和显式解,对于更好地理解复杂物理现象的机理具有重要意义。针对求解分数偏微分方程的近似解析解,提出了一些方法,例如变分迭代方法 [10] [11] ,Adomian分解法 [12] [13] ,分数子方程法 [14] [15] ,同伦摄动方法 [16] [17] [18] 。所以寻找分数阶偏微分方程新的解析解是一个重要的课题,也可为其他相关研究提供有价值的参考。同伦分析方法将问题转化为不使用摄动技术的无穷数量的线性问题,该方法利用拓扑同伦的概念生成一个收敛的级数解。同伦分析方法可应用于解决服从 Neumann边界条件的分数阶热偏微分方程 [19] 和分数阶扩散波动方程 [20] 。在 [21] 中,作者用同伦分析方法解决了不同的线性和非线性分数阶偏微分方程。
本文主要考虑基于Sumudu变换和同伦分析方法结合的分析方法,以提供在Riemann-Liouville和Caputo意义上的一类时间分数阶偏微分方程的一种新的近似解析解。
2. 预备知识
本节简要描述了利用分数阶微积分的理论来获得解决方案的思想,从而为本文所涉及问题的解决方案提供理论基础。本节描述了Caputo导数、Riemann-Liouville分数阶积分、Sumudu变换以及Mittag-Leffle 函数的的基本定义,并且对一些分数阶导数的扩展也做了简要地介绍。
定义2.1 [22] [23] :函数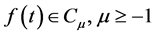 ,其中
,其中 ,对其左边进行
,对其左边进行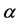 阶Riemann-Liouville积分操作的定义如下:
阶Riemann-Liouville积分操作的定义如下:
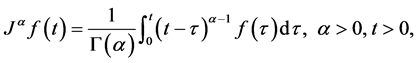
且
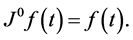
定义2.2 [24] :对于函数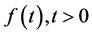 ,若存在一个实数
,若存在一个实数 ,使得
,使得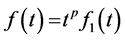 ,其中
,其中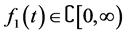 ,那么就说
,那么就说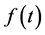 属于空间
属于空间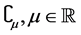 ,若
,若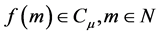 ,我们就说
,我们就说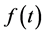 属于空间
属于空间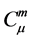 。
。
定义2.3 [25] :函数 的左Caputo导数定义如下:
的左Caputo导数定义如下:
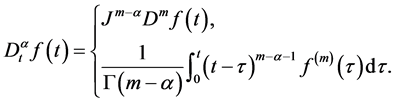
其中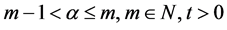 。
。
定义2.4 [26] :对Caputo分数阶导数的Sumudu变换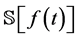 定义如下:
定义如下:
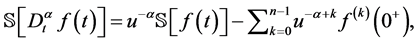
其中
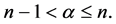
定义2.5 [27] :Jihuan He的分数阶导数定义如下:
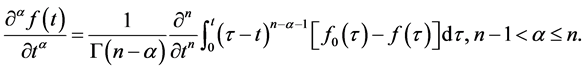
定义2.6 [26] :在90年代早期,Watugala介绍了一种初始的积分变换。函数集

上的Sumudu变换定义如下:
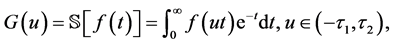
定义2.7 [26] :当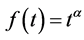 时,Sumudu变换的定义如下:
时,Sumudu变换的定义如下:
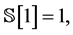
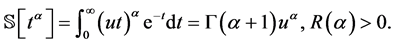
定义2.8 [28] :Mittag-Leffler函数是指数函数的推广,定义为:
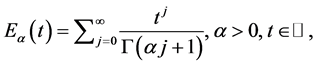
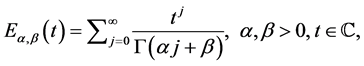
Mittag-Leffler函数的一些特殊例子如下:
1、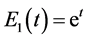 ,
,
2、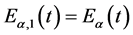 。
。
3. 同伦分析Sumudu变换方法的基本思想
本节考虑以下方程 [29] :
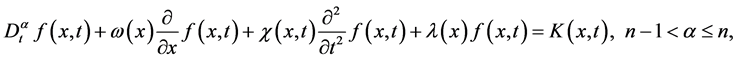 (1)
(1)
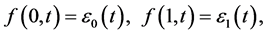
对方程(1)的两边做Sumudu变换,我们得到
 (2)
(2)
再对方程(2)的两边使用定义2.4,我们得到
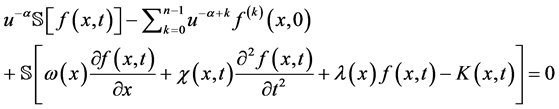 (3)
(3)
定义如下非线性算子:
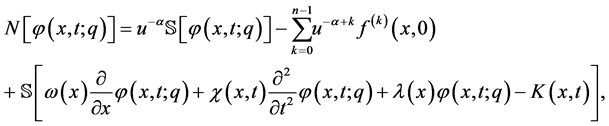 (4)
(4)
其中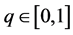 是一个嵌入参数,
是一个嵌入参数, 是一个与
是一个与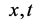 和
和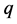 有关的实函数。构造如下同伦
有关的实函数。构造如下同伦
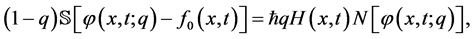 (5)
(5)
其中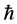 是一个非零辅助参数,
是一个非零辅助参数,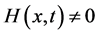 是辅助函数,
是辅助函数,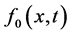 是未知函数
是未知函数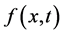 的初始猜测。辅助参数的选择对同伦分析Sumudu变换方法具有很重要的意义。观察方程(5),当
的初始猜测。辅助参数的选择对同伦分析Sumudu变换方法具有很重要的意义。观察方程(5),当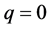 或
或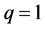 时 [26]
时 [26]
 (6)
(6)
当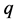 从0变换到1时,方程的解就从初始推论
从0变换到1时,方程的解就从初始推论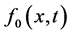 收敛到解
收敛到解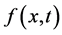 。
。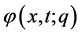 在
在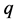 处的泰勒展式 [26] 如下:
处的泰勒展式 [26] 如下:
 (7)
(7)
其中
 (8)
(8)
级数解(7)的收敛性依赖于初始猜测、辅助线性算子和辅助函数。级数(7)收敛于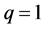 。因此,我们得到
。因此,我们得到
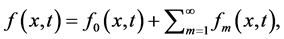 (9)
(9)
这是原方程的一个解。上面的表达式为我们提供了初始猜测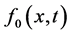 和精确解
和精确解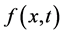 之间的联系,即
之间的联系,即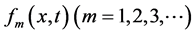 ,其表达式有待确定。
,其表达式有待确定。
定义矢量
 (10)
(10)
对方程(5)中的参数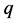 做
做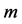 阶导数后取
阶导数后取 ,最后再除以
,最后再除以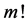 ,得
,得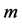 阶形变方程如下:
阶形变方程如下:
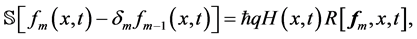 (11)
(11)
其中
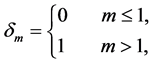 (12)
(12)
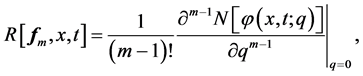 (13)
(13)
用这种方法,简单获取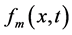 其中
其中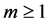 。因此可得:
。因此可得:
 (14)
(14)
其中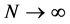 ,(14)既是方程(1)的简单近似解。
,(14)既是方程(1)的简单近似解。
4. 数值算例
本节我们将通过一些数值算例来验证同伦分析Sumudu变换方法的有效性和精确性。
例4.1
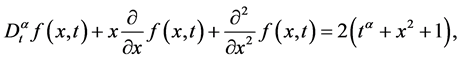 (15)
(15)
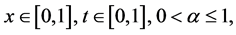
边界条件:
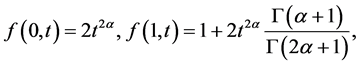
初始条件:

方程(15)的精确解
 (16)
(16)
对方程(15)的两边做Sumudu变换,我们得到
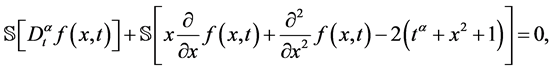 (17)
(17)
再对方程(17)的两边使用定义2.4,我们得到
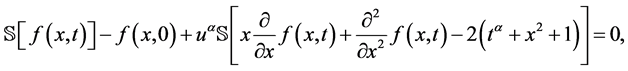
非线性算子定义如下:
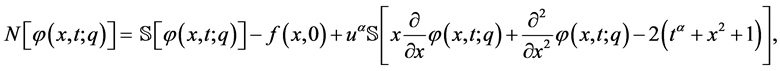
得到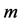 阶形变方程后应用Sumudu变换的逆变换,我们可以得到:
阶形变方程后应用Sumudu变换的逆变换,我们可以得到:
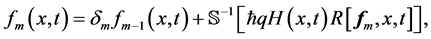 (18)
(18)
其中
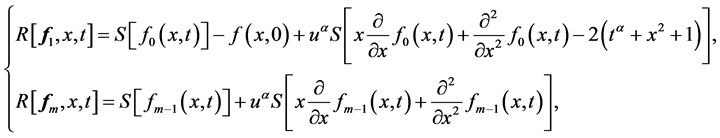 (19)
(19)
由于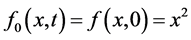 ,令
,令 ,由方程(18)及方程(19)可得到方程(15)的近似解析解,这里
,由方程(18)及方程(19)可得到方程(15)的近似解析解,这里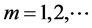 ,我们可以得到:
,我们可以得到:
 ,
,
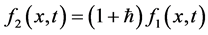 ,
,
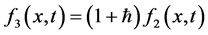 ,
,
等。以同样的方式,可以获得方程(15)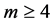 的其他部分。方程(15)的解是由下式可得,
的其他部分。方程(15)的解是由下式可得,
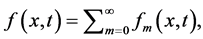
同伦分析Sumudu变换方法级数解的精度和收敛性取决于辅助参数的仔细选择。在这里,我们选择 ,即可得:
,即可得:
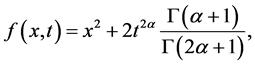 (20)
(20)
其中方程(20)与方程(16)相等。
例4.2
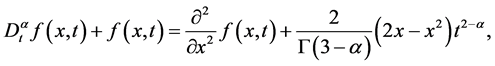 (21)
(21)
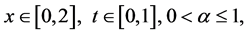
边界条件:

初始条件:
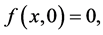
方程(21)的精确解为:
 (22)
(22)
对方程(21)的两边做Sumudu变换,我们得到
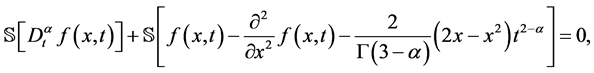 (23)
(23)
再对方程(23)的两边使用定义2.4,我们得到

定义非线性算子如下:
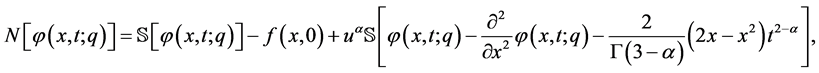
得到 阶形变方程后应用Sumudu变换的逆变换,我们可以得到:
 (24)
(24)
其中
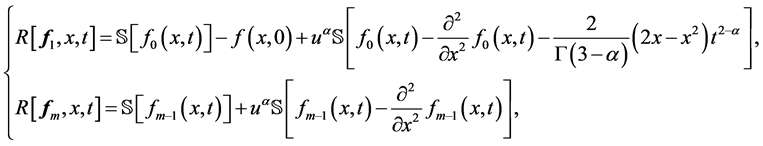 (25)
(25)
由于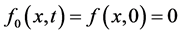 ,令
,令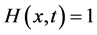 ,由方程(24)及方程(25)可得到方程(21)的近似解析解,这里
,由方程(24)及方程(25)可得到方程(21)的近似解析解,这里 ,我们可以得到:
,我们可以得到:
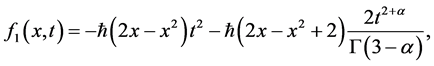

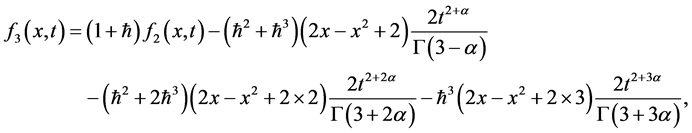
等。以同样的方式,可以获得方程(21) 的其他部分。方程(21)的解是由下式可得,
的其他部分。方程(21)的解是由下式可得,

其中我们选择 ,即可得:
,即可得:

当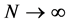 ,将用到以下解决方案:
,将用到以下解决方案:
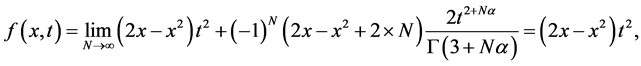 (26)
(26)
此结果与原方程精确解相等。
例4.3 考虑时间分数阶Klein-Gordon方程
 (27)
(27)
初始条件:
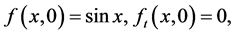 (28)
(28)
方程(27)的精确解
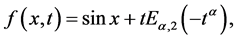 (29)
(29)
对方程(27)的两边做Sumudu变换,我们得到
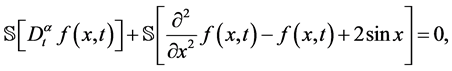 (30)
(30)
再对方程(30)的两边使用定义2.4,我们得到

定义非线性算子如下:

得到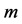 阶形变方程后应用Sumudu变换的逆变换,我们可以得到:
阶形变方程后应用Sumudu变换的逆变换,我们可以得到:
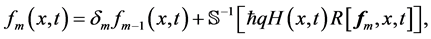 (31)
(31)
其中
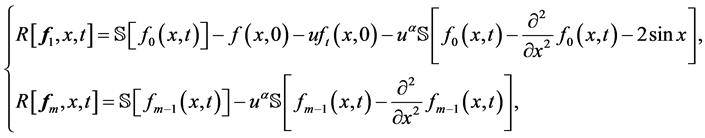 (32)
(32)
由于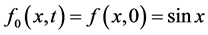 ,令
,令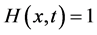 ,由方程(31)及方程(32)可得到方程(27)的近似解析解,这里
,由方程(31)及方程(32)可得到方程(27)的近似解析解,这里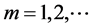 ,我们可以得到:
,我们可以得到:

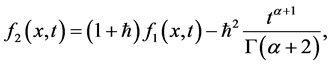
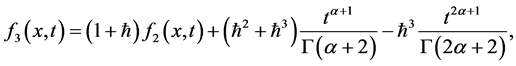
等。以同样的方式,可以获得方程(27)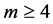 的其他部分。方程(27)的解是由下式可得,
的其他部分。方程(27)的解是由下式可得,
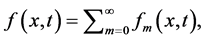
选择 ,即可得:
,即可得:
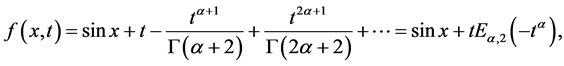 (33)
(33)
此结果与原方程的精确解相等。
方程(33)中若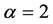 ,则
,则
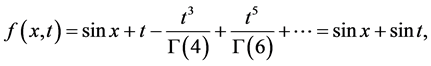
此结果与方程(28)完全一致。
例4.4
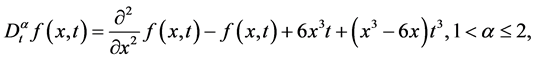 (34)
(34)
具有以下初始条件:
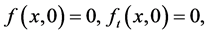 (35)
(35)
若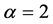 ,方程(34)的精确解为:
,方程(34)的精确解为:
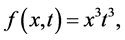 (36)
(36)
对方程(34)的两边做Sumudu变换,我们得到
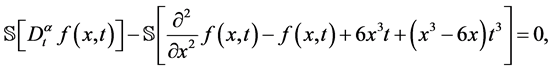 (37)
(37)
再对方程(37)的两边使用定义2.4,我们得到
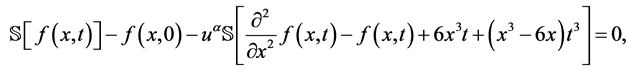
非线性操作如下:

得到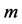 阶形变方程后应用Sumudu变换的逆变换,我们可以得到:
阶形变方程后应用Sumudu变换的逆变换,我们可以得到:
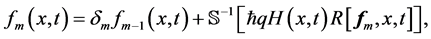 (38)
(38)
其中
 (39)
(39)
由于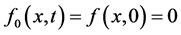 ,令
,令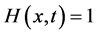 ,由方程(38)及方程(39)可得到方程(34)的近似解析解,这里
,由方程(38)及方程(39)可得到方程(34)的近似解析解,这里 ,我们可以得到:
,我们可以得到:
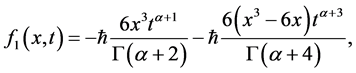

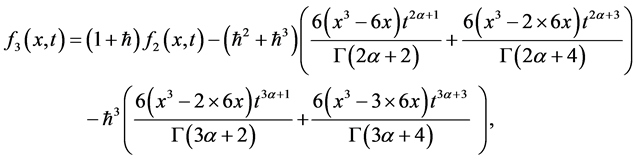
等。以同样的方式,可以获得方程(34)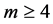 的其他部分。方程(34)的解是由下式可得,
的其他部分。方程(34)的解是由下式可得,
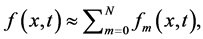
选择 ,即可得:
,即可得:

当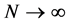 ,将用到以下解决方案:
,将用到以下解决方案:
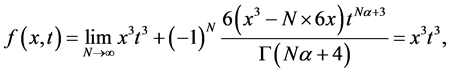 (40)
(40)
此结果与方程(36)相等。
5 结论
本文主要介绍了一种求解时间分数阶问题的方法,该方法基于同伦分析和Sumudu变换的结合,并且已成功地应用于求解齐次和非齐次微分方程。对于非齐次方程,如果非齐次项是每个变量多项式之和,则其近似解与精确解基本一致。这种新方法的一个重要优点是运算量低。它可以用来快速求解时间分数阶和整数阶方程。
基金项目
国家自然科学基金项目(No.11461072),新疆维吾尔自治区杰出青年科技人才培养项目(No.QN2016JQ0367),新疆师范大学数学校级重点学科。
文章引用
杨博慧,张新东. 一类时间分数阶偏微分方程的同伦分析Sumudu变换解法
Homotopy Analysis Sumudu Transform Method for Solving a Class of Time Fractional Partial Differential Equations[J]. 理论数学, 2017, 07(04): 322-333. http://dx.doi.org/10.12677/PM.2017.74042
参考文献 (References)
- 1. Waleed, H. (2013) Solving nth Order Integro Differential Equations Using the Combined Laplace Transform Adomian Decomposition Method. Applied Mathematics, 4, 882-886.
- 2. Weerakoon, S. (1994) Application of Sumudu Transform to Partial Differential Equations. International Journal of Mathematical Education in Science and Technology, 25, 277-283. https://doi.org/10.1080/0020739940250214
- 3. Belgacem, F.B.M. (2010) Sumudu Transform Applications to Bessel Functions and Equations. Applied Mathematical Sciences, 4, 3665-3686.
- 4. Gupta, V.G., Sharma, B. and Belgacem, F.B.M. (2011) On the Solutions of Generalized Fractional Kinetic Equations. Applied Mathematical Sciences, 5, 899-910.
- 5. Katatbeh, Q.D. and Belgacem, F.B.M. (2011) Applications of the Sumudu Transform to Fractional Differential Equations. Nonlinear Studies, 18, 99-112.
- 6. Guerrero, F., Santonja, F.J. and Villanueva, R.J. (2013) Solving a Model for the Evolution of Smoking Habit in Spain with Homotopy Analysis Method. Nonlinear Analysis: Real World Applications, 14, 549-558. https://doi.org/10.1016/j.nonrwa.2012.07.015
- 7. Jafari, H. and Firoozjaee, M.A. (2010) Multistage Homotopy Analysis Method for Solving Non-Linear Riccati Differential Equations. International Journal of Research and Reviews in Applied Sciences, 4, 128-132.
- 8. Elsaid, A. (2011) Homotopy Analysis Method for Solving a Class of Fractional Partial Differential Equations. Communications in Nonlinear Science and Numerical Simulation, 16, 3655-3664. https://doi.org/10.1016/j.cnsns.2010.12.040
- 9. Mohyud-Din, S.T., Yldrm, A. and Ylkl, E. (2012) Homotopy Analysis Method for Space- and Time-Fractional Kdv Equation. International Journal of Numerical Methods for Heat & Fluid Flow, 22, 928-941. https://doi.org/10.1108/09615531211255798
- 10. Das, N., Singh, R., Wazwaz, A.M. and Kumar, J. (2016) An Algorithm Based on the Variational Iteration Technique for the Bratu-Type and the Lane-Emden Problems. Journal of Mathematical Chemistry, 54, 527-551. https://doi.org/10.1007/s10910-015-0575-6
- 11. Mistry, P.R. and Pradhan, V.H. (2015) Approximate Analytical Solution of Non-Linear Equation in One Dimensional Instability Phenomenon in Homogeneous Porous Media in Horizontal Direction by Variational Iteration Method. Procedia Engineering, 127, 970-977. https://doi.org/10.1016/j.proeng.2015.11.445
- 12. Duan, J.S., Rach, R. and Wazwaz, A.M. (2015) Steady-State Concentrations of Carbon Dioxide Absorbed into Phenyl Glycidyl Ether Solutions by the Adomian Decomposition Method. Journal of Mathematical Chemistry, 53, 1054-1067. https://doi.org/10.1007/s10910-014-0469-z
- 13. Lu, L., Duan, J. and Fan, L. (2015) Solution of the Magnetohydrodynamics Jeffery-Hamel FFOW Equations by the Modiffed Adomian Decomposition Method. Advances in Applied Mathematics and Mechanics, 7, 675-686. https://doi.org/10.4208/aamm.2014.m543
- 14. Ma, H.C., Yao, D.D. and Peng, X.F. (2015) Exact Solutions of Non-Linear Fractional Partial Differential Equations by Fractional Sub-Equation Method. Thermal Science, 19, 1239-1244. https://doi.org/10.2298/TSCI1504239M
- 15. Mohyud-Din, S.T., Nawaz, T., Azhar, E. and Akbar, M.A. (2015) Fractional Sub-Equation Method to Space-Time Fractional Calogero-Degasperis and Potential Kadomtsev-Petviashvili Equations. Journal of Taibah University for Science, 11, 258-263.
- 16. Nino, U.F., Leal, H.V., Khan, Y., Díaz, D.P., Sesma, A.P., Fernández, V.J. and Orea, J.S. (2014) Modiffed Nonlinearities Distribution Homotopy Perturbation Method as a Tool to FFND Power Series Solutions to Ordinary Differential Equations. Springerplus, 3, 1-13.
- 17. Cuce, E. and Cuce, P.M. (2015) A Successful Application of Homotopy Perturbation Method for Efficiency and Effectiveness Assessment of Longitudinal Porous FFNS. Energy Conversion and Management, 93, 92-99. https://doi.org/10.1016/j.enconman.2015.01.003
- 18. Sayevand, K. and Jafari, H. (2016) On Systems of Nonlinear Equations: Some Modified Iteration Formulas by the Homotopy Perturbation Method with Accelerated Fourth-And FFFTH-Order Convergence. Applied Mathematical Modelling, 40, 1467-1476. https://doi.org/10.1016/j.apm.2015.06.030
- 19. Xu, H., Liao, S.J. and You, X.C. (2009) Analysis of Nonlinear Fractional Partial Differential Equations with the Homotopy Analysis Method. Communications in Nonlinear Science and Numerical Simulation, 14, 1152-1156. https://doi.org/10.1016/j.cnsns.2008.04.008
- 20. Jafari, H. and Seiff, S. (2009) Homotopy Analysis Method for Solving Linear and Nonlinear Fractional Diffusion- Wave Equation. Communications in Nonlinear Science and Numerical Simulation, 14, 2006-2012. https://doi.org/10.1016/j.cnsns.2008.05.008
- 21. Jafari, H. and Seiff, S. (2009) Solving a System of Nonlinear Fractional Partial Differential Equations Using Homotopy Analysis Method. Communications in Nonlinear Science and Numerical Simulation, 14, 1962-1969. https://doi.org/10.1016/j.cnsns.2008.06.019
- 22. Luchko, Y. and Gorenflo, R. (1999) An Operational Method for Solving Fractional Differential Equations with the Caputo Derivatives. Acta Mathematica Vietnamica, 24, 207-233.
- 23. Moustafa, O.L. (2003) On the Cauchy Problem for Some Fractional Order Partial Differential Equations. Chaos, Solitons & Fractals, 18, 135-140. https://doi.org/10.1016/S0960-0779(02)00586-6
- 24. Pandey, R.K. and Mishra, H.K. (2016) Homotopy Analysis Fractional Sumudu Transform Method for Time Fractional Third Order Dispersive Partial Differential Equation. Advances in Computational Mathematics, 43, 365-383.
- 25. Oldham, K.B. and Spanier, J. (1974) The Fractional Calculus: Theory and Application of Differentiation and Integration to Arbitrary Order. Academic Press, New York and London.
- 26. Belgacem, F.B.M. and Karaballi, A.A. (2006) Sumudu Transform Fundamental Properties Investigations and Applications. Journal of Applied Mathematics and Stochastic Analysis, 2006, 1-23. https://doi.org/10.1155/JAMSA/2006/91083
- 27. HE. J.H. (2014) A Tutorial Review on Fractal Space Time and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718. https://link.springer.com/article/10.1007/s10773-014-2123-8
- 28. Kilbas, A.A., Saigo, M. and Saxena, R.K. (2004) Generalized Mittag-Leffler Function and Generalized Fractional Calculus Operators. Integral Transforms and Special Functions, 15, 31-49. https://doi.org/10.1080/10652460310001600717
- 29. Morales-Delgado1, V.F., Gómez-Aguilar, J.F., Yépez-Martínez, H., Baleanu, D., Escobar-Jimenez, R.F. and Olivares- Pregrino, V.H. (2016) Laplace Homotopy Analysis Method for Solving Linear Partial Differential Equations Using a Fractional Derivative with and without Kernel Singular. Advances in Difference Equations, 164, 1-17. https://doi.org/10.1186/s13662-016-0891-6