Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30296
,
7
pages
10.12677/PM.2019.93046
A New Method to Prove Mathematical Conjecture of D-Finite Class
—Talking about the Differential Theorem of Morley Triangle
Jun Yang1, Zhicheng Guo2*
1Beijing Institute of Technology, Zhuhai, Zhuhai Guangdong
2Northern Design and Research Institute, Shijiazhuang Hebei

Received: Apr. 25th, 2019; accepted: May 5th, 2019; published: May 20th, 2019

ABSTRACT
This paper presents and proves the Morley differential theorem (Gauss curvature pointer fineness theorem) based on Morley’s theorem. According to the conclusion of the three-point collinearity of this theorem, a correlation model between the right triangle and its mirror image and the Möbius function is constructed, which lays a foundation for the further study of the interpolation algorithm and discrete properties of the Möbius function. This theorem reveals that the nature of functional is functional “one-dimensional”, which lays a foundation for further extending the geometric properties of functional one-dimensional to functional “plane”. The theorems, corollaries and open problems in this paper reveal the properties of limit cycles of vector fields of first order polynomials and the research approaches of vector fields of quadratic polynomials. The new method to prove non-commutative D-finite class conjectures is given.
Keywords:Morley’s Triangles, Gaussian Curvature, D-Finite, Conformal Mappings
证明D-Finite类数学猜想的新方法
——从Morley三角形的微分定理谈起
杨 军1,郭志成2*
1北京理工大学珠海学院,广东 珠海
2北方设计研究院,河北 石家庄

收稿日期:2019年4月25日;录用日期:2019年5月5日;发布日期:2019年5月20日

摘 要
提出并证明了基于Morley三分线定理的Morley三角形微分定理(Gauss曲率指针细数定理)。根据该定理三点共线的结论构建了直角三角形及其镜像与Möbius函数对应的关联模型,为进一步研究Möbius函数的插值算法和离散性质奠定了基础;该定理还揭示了泛函的本质是泛函“一维”,并为进一步将泛函一维的几何性质推广到泛函“平面”指出了研究方向;论文中的定理、推论和开放性问题揭示了一次多项式向量场的极限环性质和二次多项式向量场的研究途径。给出了证明非交换D-finite类猜想的新方法。
关键词 :Morley三角形,高斯曲率,D-有限,共形映射

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Galois群论告诉我们:采用几何作图(有限次)的方法不能画出一个任意角的三等分线。然而有限次循环采用几何作图的方法依次画出三角形每一个内角的两等分线并逐渐逼近画出三等分线,可以得到著名的Morley三分线定理 [1] :一个三角形的三个内角的三等分线共六条线,与三角形三条边最近的两条三等分线分别相交于三点,将三点两两连线就构成了等边三角形。如图1。
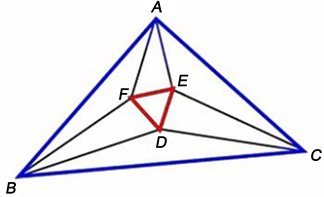
Figure 1. Morley’s equilateral triangle
图1. 莫莱的等边三角形
两等分线相交于一个点,三等分线相交于等边三角形。进一步可以画出四等分线、五等分线,一直到无穷等分线,使得分别靠近三边的等分线交点逐步接近三边并最终相交于三边上。称这三个交点所成的三角形为内等分三角形。定义内等分三角形的面积与三角形ABC面积的比值为特征值,记为 。比值 由三角形的任意两个内角和等分数n确定。
2. Gauss曲率及其指针的概念
设曲面上任意一条闭曲线L的内部有一个点k,过k点做出其密切球面,则在密切球面上存在曲线L的映射曲线 。设密切球面上由 所围成的面积为G,曲面上由L所围成的面积为F。当曲线L缩小到曲面上的k点时,F和G将趋近于零,而G与F之商将趋近于一个极限值K,称其为Gauss曲率:
称Gauss曲率的两个映射方向为指针,通常记为±1。在空间直角坐标系中,曲面上Gauss曲率的指针方向是由法线方向确定的,在所有与原曲面正交的截面中,存在彼此垂直的两个截面,它们所截曲线的曲率半径存在最大值和最小值,称它们为主曲率。Gauss曲率就是这两个主曲率的乘积。
3. Morley三分线微分定理研究
三角形三个内角的角平分线(两等分角)交于一点,此时 ,当 时,比值 由0趋近于一个定值,记为 。显然,在研究n等分内角过程中,n可以是有理数。当 时,内等分三角形的三边长度的短、中、长排序与三角形ABC三边的短、中、长的排序相反,也就是说 是最小的负值。同理,当我们选取n为2~3之间的有理数时,内等分三角形三边的短、中、长排序与三角形ABC的三边短、中、长的排序相同。这就说明了在 的地方 改变符号 [2] 。本文给出了Morley三分线定理的微分定理(图2中 三点共线可以解释为半径为无穷大的半圆周上的 弧长的微分。故称该定理是Morley三分线定理的微分定理)。该定理与Gauss曲率及其指针方向相关。
定理:设三角形∆ABC的Morley等边三角形为∆DEF (见图2),若BC和EF的延长线交于点 ,CA和FD的延长线交于点 ,AB和DE的延长线交于点 。那么,当且仅当∆ABC为直角三角形时, 三点共线。
证明:
文献 [3] 证明了

Figure 2. Morley’s triangle and opposite intersection
图2. Morley三角形与对边的交点
由此得到
设:
,那么三个角度 一正二负。
一正二负。
过
做圆,存在唯一的圆弧和圆心。当
为有理数时,n内等分三角形的 大于0,它与三个角度
的符号乘积相同,视为圆弧和圆心同向(凹多边形);当
为有理数时,n内等分三角形的
小于0,它与三个角度
的符号乘积相反,视为圆弧和圆心反向(凸多边形)。显然,当
时,圆心只能在圆弧上。
大于0,它与三个角度
的符号乘积相同,视为圆弧和圆心同向(凹多边形);当
为有理数时,n内等分三角形的
小于0,它与三个角度
的符号乘积相反,视为圆弧和圆心反向(凸多边形)。显然,当
时,圆心只能在圆弧上。
对于直角三角形,设 ,那么 由直角三角形的一个锐角确定,是单变量函数。 的正负号又可以由三个角 的乘积确定。显然,当直角三角形逐步变为等腰直角三角形时, ,圆弧弧长为 ,它恰是 的正负号变化的地方。此时 的连线是有限长度,它相对于平行直线 是一个点。根据文献 [3] 给出的定理和反证法原理, 三点必共线,否则与有理数 无限稠密相矛盾。+
当
时,n等分三角形∆ABC内角的靠近三边的三个交点
位于三角形的三边上,且三角形∆A1B1C1的边长的长短顺序与三角形∆ABC的边长的长短顺序相反。如果继续 等分新三角形∆A1B1C1的内角,当
时,重复上述过程就得到与三角形∆ABC的边长的长短顺序相同的第二个新三角形∆A2B2C2。如果把这个过程重复无穷多次(即
),则在三角形∆ABC的内部得到了一个定点,记为 。
等分新三角形∆A1B1C1的内角,当
时,重复上述过程就得到与三角形∆ABC的边长的长短顺序相同的第二个新三角形∆A2B2C2。如果把这个过程重复无穷多次(即
),则在三角形∆ABC的内部得到了一个定点,记为 。
显然,等边三角形∆ABC的定点 是形心,但确定一般相似三角形的定点 的位置是困难的。因此进一步的首要问题是
猜想(一个开放性问题):任意三角形∆ABC的定点 都是形心吗?如何证明。
我们既可以把三角形三个有向角的等分数n共形映射到连续的实数,研究其连续的分析学性质。也可以把等分数n共形映射为素数,研究其离散的数论性质。由于Morley三分线微分定理是联系分析与代数的纽带,因此本文提出的开放性问题比许多数论猜想更重要。
4. Gauss曲率指针及其符号的细数研究
Gauss曲率指针符号的定义:三等分的内等分三角形是二元函数 的唯一改变符号的点,而 的变化与Gauss曲率的指针方向相关,因此称 为Gauss曲率的指针符号。
Gauss指针的进一步细分属于非交换D-finite生成函数的研究范畴,本文揭示了这种生成函数的本质。
当
时,曲面上某一点k始终在三角形∆ABC中,k点的曲率可以由三角形∆ABC收缩为一点得到。显然,如果直角三角形∆ABC中的线段
,那么共点直线上的线段长度 。我们用比值的乘积
或者比值的商
表示Gauss曲率指针的精细结构(或细数Fine numbers)。人们通常也把点k的Gauss曲率指针记为Möbius函数
。同理,把三角形∆ABC的镜像
收缩为一点得到的Gauss曲率指针记为Möbius函数
。
。我们用比值的乘积
或者比值的商
表示Gauss曲率指针的精细结构(或细数Fine numbers)。人们通常也把点k的Gauss曲率指针记为Möbius函数
。同理,把三角形∆ABC的镜像
收缩为一点得到的Gauss曲率指针记为Möbius函数
。
需要说明的,对于任意确定的三角形∆ABC,我们可以定义比例系数的乘积函数 和商函数
。尽管乘积函数
和商函数
并不是常数1 (它随角度等分数n而变,因此n作为自变量),而是一个无量纲(多项式主题的数学分支中,称之为幂零项)的超越函数。但是它们之间由一个有理系数的二次方程相联系,因此乘积函数
和商函数
属于二维空间的组合性质。这个性质与Gauss曲率不随曲面的弯曲而变的性质等价。
和商函数
。尽管乘积函数
和商函数
并不是常数1 (它随角度等分数n而变,因此n作为自变量),而是一个无量纲(多项式主题的数学分支中,称之为幂零项)的超越函数。但是它们之间由一个有理系数的二次方程相联系,因此乘积函数
和商函数
属于二维空间的组合性质。这个性质与Gauss曲率不随曲面的弯曲而变的性质等价。
为了说明 和 组合性质,我们摘录文献 [4] 给出的一般的Morley三分线定理的一个代数证明如下:
对于一般的三角形,有向角 可以采用 三种形式(同样处理有向角 和 )。做出三角形三个内角及其补角的三等分线,这样产生的27个三角形中有18个是等边三角形 [5] ,这种等边三角形统称为Morley三角形。
设r为∆ABC的外接圆半径,三个内角 。则有
同理
而
由对称性得到 。由此就证明了三角形内部的Morley三分线定理。更一般的Morley三角形的边长是由下面的公式得到的。
式中 的每一个都是 的一种有限制的组合选择。
由此就得到了18个是等边三角形。三角形内部的Morley三角形已经具备了所有18个Morley三角形的充分代表性,人们通常称这种代表性为特征函数、特征向量、特征值或不变量。类似的,确定边长的三角形有两种(该三角形或它的镜像)形式,可以用一个特征向量作代表。本文定理给出的是这种三角形特征向量的性质。
由于本文定理给出共线的三点来源于Morley三角形的三边与其对边的交点,因此由本文定理和文献 [6] 可以得到一个非常有用的推论:
推论:表示Gauss曲率的指针方向的函数和Möbius函数都属于二维空间的有限制的组合性质,并且函数
和 是研究这种组合性质的计算工具。
是研究这种组合性质的计算工具。
文献 [6] 在18个有理Morley三角形的证明中,采用了用向量场表示等分线的代数方法,证明过程利用了置换群的对称性原理,其本质是采用了指数项的费马递降法原理。又因为黎曼映射的对径点也属于这种组合对称性质,因此可以用本文的定理和推论研究黎曼的非平凡零点。
推论可以给出下面的论断:解决开放性问题的方法等价于(或包含了)一些数论猜想的证明。这是因为它们不仅仅是同一类问题,更是属于完全相同的限制性(即对称性)组合问题1。如等价于 Catalan数的 猜想的证明 [7] 和解决了二次域 中的非零、非单位整数表示为素元乘积的唯一性(未解决的)问题。
5. 开放性问题的现状和展望
开放性问题简单明了,但是每向前推进一步都是极其困难的,因为它属于有理数→代数→D-有限(rational → algebraic → D-finite)的数学演进过程的最后一类,等边三角形推进到等腰直角三角形也是如此。为了说清楚这一点,我们以Hilbert第16个问题为例。
Hilbert第16个问题在Hilbert提出的23个问题中进展最小。Hilbert第16个问题是正则变分问题的解是否一定解析——即任意向量场的正则图是否属于分析性质,其中的一部分是求多项式(即平面)向量场的极限环数的上界,极限环是指向量场的孤立周期轨道。
由于对于平面上分析向量场(或任意多项式向量场)图的研究可以归结为极限环数问题,因此人们通过大量的实例发现了二次多项式向量场最多有4个极限环,三次多项式向量场最少有11个极限环。除此之外,人们对极限环数的上限知之甚少,甚至至今未能证明二次系统最多只能有4个极限环。此外,也不知道任意多项式向量场是否只有有限个极限环。尽管1923年,Dulac [8] 声称证明了平面上分析向量场的所有图都是有限的(简称D-finite)。然而,现在人们普遍认为他的证明并不严密。得到人们公认的最好结论是:Chicone和Shafer [9] 在1983年证明了平面上分析向量场的有界图是有限的。
显然,本文揭示的是一次多项式向量场的极限环性质 [6] ,并指出了如何把一次多项式向量场的极限环推广到二次多项式向量场的方法和途径。具体来说,论文的主要结论由三部分(定理、推论和开放性问题——猜想)构成:定理给出了简单形式的一次多项式环的几何形式(即泛函“一维”轴)和性质,推论提出了把一次多项式环推广到二次多项式环(即泛函平面)的计算方法,本文的猜想把二次多项式向量场最多有4个极限环的猜想转化成为了一个直观的(泛函意义下的)几何猜想。
开放性问题指出了一次多项式环推广到更高次的多项式环的研究途径。因此,在研究和解决本文提出的开放性问题过程中,自然而然地将会证明(包括但不限于Hilbert第16个问题)非交换D-finite类中许多困难的猜想。
作者得到了任意直角三角形的定点 都是形心的证明,可以基本上确认开放性问题的答案是肯定的。但是由于涉及到了双线性的一般代数表达式或者四元数对称的复杂问题,不是一篇小论文可以说清楚的,故不在本文论述。
文章引用
杨 军,郭志成. 证明D-Finite类数学猜想的新方法
A New Method to Prove Mathematical Conjecture of D-Finite Class[J]. 理论数学, 2019, 09(03): 344-350. https://doi.org/10.12677/PM.2019.93046
参考文献
- 1. Morley, F. (1903) Orthocentric Properties of the Plane n-Line. Transactions of the American Mathematical Society, 4, 1-12.
https://doi.org/10.2307/1986445 - 2. Braude, E.J. (2016) Generalizing the Morley Trisector and Various Theorems with Realizability Computations. arXiv:1603.03463 [cs.CG]
- 3. Karamzadeh, O.A.S. (2014) Is John Conway’s Proof of Morley’s Theorem the Sim-plest and Free of a Deus ex Machina? The Mathematical Intelligencer, 36, 4-7.
https://doi.org/10.1007/s00283-014-9481-1 - 4. Letac, A. (1939) Solution (Morley’s Triangle), Problem No. 490. Sphinx, 9, 46.
- 5. Dobbs, W.J. (1938) Morley’s Triangle. Mathematical Gazette, 22, 50-57, and 189 for comment.
https://doi.org/10.2307/3607446 - 6. Bremner, A., Goggins, J.R., Guy, M.J.T. and Guy, R.K. (2000) On Rational Morley Triangles. Acta Arithmetica, 2, 177-187.
https://doi.org/10.4064/aa-93-2-177-187 - 7. Stanley, R P. (2015) Catalan Number. Cambridge University Press, Cambridge.
- 8. Dulac, H. (1923) Sur les Cycles Limites. Bulletin de la Société Mathématique de France, 51, 45-188.
https://doi.org/10.24033/bsmf.1031 - 9. Chicone, C. and Shafer, D.S. (1983) Separatrix and Limit Cycles of Quadratic Systems and Dulac’s Theorem. Transactions of the American Mathematical Society, 278, 585-612.
https://doi.org/10.1090/s0002-9947-1983-0701513-x
NOTES
1注:限制性条件相当于歌德尔的固定符号,等价意味着具有相同的形式演算系统“PM”。
*通讯作者。