Pure Mathematics
Vol.
11
No.
02
(
2021
), Article ID:
40533
,
6
pages
10.12677/PM.2021.112036
格点的多重可见性
黄旸
青岛大学数学与统计学院,山东 青岛

收稿日期:2021年1月13日;录用日期:2021年2月16日;发布日期:2021年2月24日

摘要
设 是二维整数格且 ,若格点 位于形如 的曲线上,且在 与原点 之间的相应曲线段上至多有 个格点(不含端点),则称 是l-重的k-可见格点。特别地,当重数 时,简称 为k-可见格点。本文给出了方形区域 中l-重k-可见格点个数的一个渐近公式,这推广了Goins等人关于k-可见格点密度的一个结果。
关键词
格点,k-可见,渐近公式

Multiple Visibility of Lattice Points
Yang Huang
School of Mathematics and Statistics, Qingdao University, Qingdao Shandong

Received: Jan. 13th, 2021; accepted: Feb. 16th, 2021; published: Feb. 24th, 2021

ABSTRACT
Let be the two dimensional integer lattice and . We say a point is k-visible with Level-l if it lies on a curve of type with and there are at most lattice points on the curve segment between points and (not included). In this paper, we prove an asymptotic formula for the number of lattice points in the square which are k-visible with Level-l. This generalizes a result of Goins et al.
Keywords:Lattice Points, k-Visibility, Asymptotic Formula

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
二维格 中的一个格点 称为是可见的,若没有其它格点位于 与 之间的直线段(不含端点)上。1883年,Sylvester [1] 证明了 中可见格点的比例为 ,其中 ,,是黎曼Zeta函数。2018年,Goins,Harris,Kubik和Mbirika [2] 将Sylvester的结果推广到了沿曲线可见的情形。格点 称为是k-可见的,若 位于形如 的曲线上,且在 与 的之间曲线段(不含端点)上没有其它格点。Goins等人证明了 中k-可见格点的比例为 ,其他相关研究可参见文献 [3] 和 [4] 等。
最近,刘奎和孟宪昌 [5] 提出了多重k-可见性的概念。对于 ,若格点 在形如 的曲线上,且在点 与 之间的曲线段(不含端点)上至多有 个格点,则称点 是l-重k-可见的(见图1)。特别地,当 时,简称 为k-可见格点;当 时,简称 是l-重可见格点。刘奎和孟宪昌给出了方形区域 中1-重和2-重k-可见格点个数的渐近公式。从他们的结果可以得到 中2-重可见格点的密度为 。
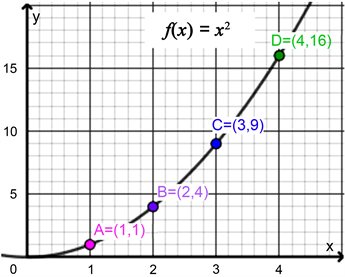 格点A:1-重2-可见;格点A,B:2-重2-可见;格点A,B,C:3-重2-可见;格点D:非3-重2-可见。
格点A:1-重2-可见;格点A,B:2-重2-可见;格点A,B,C:3-重2-可见;格点D:非3-重2-可见。
Figure 1. Higher level 2-visible lattice points along a curve
图1. 沿曲线的多重2-可见格点
本文主要考虑更高重数的k-可见格点。对于 ,定义
为 中l-重k-可见格点的集合。
定理1.1. 对于任意的 和给定的 ,则
.
注:由于格点的可见性在四个象限里是对称分布的,因此由定理1.1可知,格 中l-重k-可见格点的密度为 。由此及黎曼Zeta函数的定义可知,当l趋于无穷时,该密度趋于1,符合直观。特别地,当 时,定理1.1分别覆盖了上述Goins等人 [2] 以及刘奎和孟宪昌 [5] 的相应结果。
我们还对l-重k-可见格点的密度进行了数值实验(见表1),实验结果与理论结果十分吻合。
Table 1. The density of l-level k-visible points
表1. l-重k-可见格点的密度
根据定理1.1,容易得到以下推论。
推论. 对于给定的 ,格 中l-重可见格点的密度为 。
符号说明:
以下是对本文用到的符号的说明。
2. 准备知识
以下广义最大公约数的定义是由Goins等人在 [2] 中提出的。
定义2.1.对 ,与参数k有关的广义最大公约数定义为
.
在证明l-重k-可见格点的判别法则之前,我们先证明以下引理。
引理2.1. 对任意 ,,我们有
且 当且仅当 。
证明:若 且 。设 ,。根据 的定义,我们知道d是使得 且 的最大正整数,显然有 。否则,若 ,则由 ,,我们有 。同样,由 ,,我们有 。而显然 ,这与 矛盾。
反之。若 ,设 ,则有 。令 ,由 的定义,有 ,,从而有 ,。
以下l-重k-可见格点的判别法则是证明定理1.1的关键。
引理2.2. 对 ,任意整数 。格点 位于曲线 上,则在点 与点 之间的曲线段上恰好有 个整数格点当且仅当 。
证明:假设 。当 时,点 与点 之间的曲线段(不含端点)上恰好有0个整数格点,即格点 关于原点k-可见,当且仅当 。详细证明细节见( [2],命题3)。
当 时。位于曲线 的连接点 与点 的曲线段(不含端点)上任意整数格点 可以用以下参数形式表示出来:
,
,。t的所有可能取值的个数即为点 与点 之间的曲线段(不含端点)上的整数格点数。
设 ,。 ,则必有 ,,因而有 ,。由引理1.1可知, ,即 。则 为t的全部可能取值。由此得证。
我们还需要用到以下两个熟知的公式。
引理2.3. ( [6],定理2.1)设 是莫比乌斯函数,则对任意整数 ,有
引理2.4. ( [6],定理3.2)对 ,有
,
其中 是欧拉常数。
3. 定理1.1的证明
设 。由l-重k-可见格点的定义,并运用引理1.2,区域 中l-重k-可见格点数可表示为
, (1)
其中
,
。运用引理1.3,得
.
交换求和顺序,得到
.
因为同余式 且 的解数为 ,同余式 且 的解数为 。因此,我们有
.
余项中对 取绝对值,整理得
.
下面整理一下这3个余项。应用引理1.4,第一个余项可得如下估计
.
当 时,第二个余项与第一个余项估计结果相同; 时,由于 是一个收敛级数,因此 ,从而
。
故而有
。
扩大上式中求和的范围,得到
。
由于 ,因此
。
又因为 ,因此,
,
。将 ,,代入(1)式,定理得证。
基金项目
由国家自然科学基金(项目编号:NSFC12071238)资助。
文章引用
黄 旸. 格点的多重可见性
Multiple Visibility of Lattice Points[J]. 理论数学, 2021, 11(02): 271-276. https://doi.org/10.12677/PM.2021.112036
参考文献
- 1. Sylvester, J.J. (1883) Sur le nombre de fractions ordinaires inegales quon peut exprimer en se servant de chiffffres quinexcedent pas un nombre donne. Comptes Rendus de l’Académie des Sciences Paris XCVI: 409413.
- 2. Goins, E.H., Harris, P.E., Kubik, B. and Mbirika, A. (2018) Lattice Point Visibility on Generalized Lines of Sight. American Mathematical Monthly, 125, 593-601. https://doi.org/10.1080/00029890.2018.1465760
- 3. Benedetti, C., Estupinan, S. and Harris, P.E. (2020) Generalized Lattice Point Visibility. https://arxiv.org/abs/2001.07826
- 4. Harris, P.E. and Omar, M. (2018) Lattice Point Visibility on Power Func-tions. Integers, 18, 1-7.
- 5. Liu, K. and Meng, X.C. (2020) Visible Lattice Points along Curves. The Ramanujan Journal, 1-14. https://doi.org/10.1007/s11139-020-00302-w
- 6. Apostol, T.M. (1976) Introduction to Analytic Number Theory. Springer, New York. https://doi.org/10.1007/978-1-4757-5579-4
