上海理工大学理学院，上海

收稿日期：2023年3月17日；录用日期：2023年4月18日；发布日期：2023年4月26日

摘要

Bloch曾经提出：相应于每一个Picad型定理，必有一个相应的正规定则。这个原理对正规族理论的发展起到了重要的作用。在此基础上，利用亚纯函数值分布理论、线性代数理论及第二基本定理研究方法，研究了分担小函数的正规定则。得到如下结论：设 $\mathcal{F}$ 是 $D\subset ℂ$ 上的一族亚纯函数， $a_1\left(z\right)$ ， $a_2\left(z\right)$ ， $a_3\left(z\right)$ 在D上全纯，且满足 $\underset{z\in D}{min}\left|a_i\left(z\right)-a_j\left(z\right)\right|\ge \delta >0$ ， $1\le i<j\le 3$ 。若对 $\forall f\in \mathcal{F}$ ，有 $f\left(z\right)=a_i\left(z\right)\iff f^{\prime }\left(z\right)=a_i\left(z\right)$ ，则 $\mathcal{F}$ 在D上正规。该结论拓展了思路，将小函数和正规族以及分担值结合在一块，对后续的研究提供了思维和方法。

关键词

正规族，小函数，亚纯函数，正规定则

Research on the Normal Rule of Sharing Small Functions

Yao Wang

College of Science, University of Shanghai for Science and Technology, Shanghai

Received: Mar. 17^th, 2023; accepted: Apr. 18^th, 2023; published: Apr. 26^th, 2023

ABSTRACT

Bloch once proposed that there must be a corresponding normal rule for every Picad type theorem. This principle plays an important role in the development of normal family theory. On this basis, using the meromorphic function value distribution theory, linear algebra theory and the second basic theorem research method, the normal rule of sharing small functions is studied. The following conclusions are obtained: Let $\mathcal{F}$ is a family of meromorphic functions of a domain $D\subset ℂ$ , $a_1\left(z\right)$ , $a_2\left(z\right)$ , $a_3\left(z\right)$ is holomorphic on D, and they satisfied $\underset{z\in D}{min}\left|a_i\left(z\right)-a_j\left(z\right)\right|\ge \delta >0$ , $1\le i<j\le 3$ . Assume the condition hold for every $f\in \mathcal{F}$ , that $f\left(z\right)=a_i\left(z\right)\iff f^{\prime }\left(z\right)=a_i\left(z\right)$ , then $\mathcal{F}$ is normal on D.

Keywords:Normal Family, Small Functions, Meromorphic Function, Regular Rule

Copyright © 2023 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

Bloch曾经提出：相应于每一个Picard型定理，必有一个相应的正规定则。这个原理对正规族理论的发展起到了重要的作用，以色列数学家L. Zalcman在一定条件下证明了这个原理。在此基础上，庞学诚曾对Bloch原理进行了研究，主要讨论正规定则和正规函数的联系。

W. Schwick [1] 曾经证明：

定理1 设 $\mathcal{F}$ 为单位圆盘 $\Delta$ 上的一族亚纯函数， $a_1,a_2,a_3$ 为互不相同的有限复数，若对 $\forall f\in \mathcal{F}$ ，

${\bar{E}}_f\left(a_i\right)={\bar{E}}_{f^{\prime }}\left(a_i\right),i=1,2,3$

则称 $\mathcal{F}$ 在 $\Delta$ 上正规。

注1 庞学诚和Zalcman [2] 证明了在f和 $f^{\prime }$ 分担两个有限复数的条件下，定理结论仍然成立。

庞学诚 [3] 在此基础上证明了：

定理2 设 $\mathcal{F}$ 为单位圆盘 $\Delta$ 上的一族亚纯函数， $a_1,a_2,a_3$ 为互不相同的有限复数，若对每一个 $f\in \mathcal{F}$ ，

${\bar{E}}_f\left(a_i\right)={\bar{E}}_{f^{\prime }}\left(a_i\right),i=1,2,3$

在 $\Delta$ 内成立，则存在正数M，使得对每一个 $f\in \mathcal{F}$ ，有

$\left(1-{\left|z\right|}^2\right)\frac{\left|f^{\prime }\left(z\right)\right|}{1+{\left|f\left(z\right)\right|}^2}\le M$ ,

其中M仅与 $a_1,a_2,a_3$ 有关。

本文主要证明了：

定理 设 $\mathcal{F}$ 是 $D\subset ℂ$ 上的一族亚纯函数， $a_1\left(z\right)$ ， $a_2\left(z\right)$ ， $a_3\left(z\right)$ 在D上全纯，且满足 $\underset{z\in D}{\min }\left|a_i\left(z\right)-a_j\left(z\right)\right|\ge \delta >0$ ， $1\le i<j\le 3$ 。若对 $\forall f\in \mathcal{F}$ ，有 $f\left(z\right)=a_i\left(z\right)\iff f^{\prime }\left(z\right)=a_i\left(z\right)$ ，则 $\mathcal{F}$ 在D上正规。

该定理推广了以上两个定理，将正规族与小函数和分担值联系在一块，为再深入的研究正规族理论提供了思路和方法，不过可惜的是，由于正规族较抽象，在本文中没有找到合适的例子。

本文安排如下：第二节介绍有关定义和概念，第三节介绍主要引理，第四节为本文定理的证明。

2. 定义与概念

首先，我们回顾一些关于 ${\mathbb{P}}^N\left(ℂ\right)$ 的定义与符号。

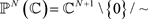是N维复射影空间，且对任意的 $x=\left(x_0,x_1,\cdots ,x_N\right)$ ， $y=\left(y_0,y_1,\cdots ,y_N\right)\in {ℂ}^{N+1}\backslash \left\{0\right\}$ ， $x~y$ 当且仅当存在某个 $\lambda \in {ℂ}^{*}$ ，使得 $\left(x_0,x_1,\cdots ,x_N\right)=\lambda \left(y_0,y_1,\cdots ,y_N\right)$ 。 $\left(x_0,x_1,\cdots ,x_N\right)$ 的等价类记作 $\left[x_0:x_1:\cdots :x_N\right]$ ，则 ${\mathbb{P}}^N\left(ℂ\right)=\left\{x=\left[x_0:x_1:\cdots :x_N\right]:x=\left(x_1,x_2,\cdots ,x_N\right)\in {ℂ}^{N+1}\backslash \left\{0\right\}\right\}$ 。

定义2.1 设 $f\left(z\right)$ 为单位圆盘 $\Delta$ 上的一个亚纯函数，若存在正数M，使得

$\left(1-{\left|z\right|}^2\right)\frac{\left|f^{\prime }\left(z\right)\right|}{1+{\left|f^{\prime }\left(z\right)\right|}^2}\le M$

称 $f\left(z\right)$ 为单位圆盘 $\Delta$ 上的一个正规函数。

定义2.2 设 $f,g$ 为区域D上的两个亚纯函数，若对复数c，

${\bar{E}}_f\left(c\right)={\bar{E}}_g(\; c\; )$

称f与g在D上分担c，其中 ${\bar{E}}_f\left(c\right)=\left\{z:f\left(z\right)=c\right\}$ 。

3. 主要引理

引理3.1 [4] 设 $\mathcal{F}$ 是一族从 ${ℂ}^m$ 中的双曲区域 $\Omega$ 映到 ${\mathbb{P}}^N\left(ℂ\right)$ 的全纯映射。 $\mathcal{F}$ 在 $\Omega$ 上不正规当且仅当存在子列 $\left\{f_n\right\}\subset \mathcal{F}$ ，点列 $\left\{z_n\right\}\subset \Omega$ 满足 $z_n\to z_0\in \Omega$ ，正数列 $\left\{{\rho }_n\right\}$ 满足 ${\rho }_n\to 0^{+}$ ，使得 $g_n\left(\xi \right):=f_n\left(z_n+{\rho }_n\xi \right)$ 在 ${ℂ}^m$ 上内闭一致收敛于从 ${ℂ}^m$ 映到 ${\mathbb{P}}^N\left(ℂ\right)$ 的非常值全纯映射 $g\left(\xi \right)$ 。

在证明主要定理的过程中，还需要如下Hurwitz定理。

引理3.2 [5] 设 $\left\{f_n\left(z\right)\right\}$ 是定义在区域 $D\subset ℂ$ 内的一列全纯函数， $a\in ℂ$ 是任意一个复数，且设 $f_n\left(z\right)$ 在D的任意一个紧子集上一致收敛于非常值的全纯函数 $f\left(z\right)$ 。若存在点 $z_0\in D$ ，使得 $f\left(z_0\right)=a$ ，则对于每一个充分大的n，方程 $f_n\left(z\right)=a$ 在D内有根。此外，存在 $z_0$ 的某领域U，使得 $f\left(z\right)-a$ 在U内根的总数与 $f_n\left(z\right)-a$ 在U内根的总数相同(计重数)。

注1 当 $n\to \infty$ 时， $f_n\left(z\right)-a$ 在U的所有零点都会收敛到 $z_0$ 。

由Nevanlinna第二基本定理，有如下引理：

引理3.3 [6] 设 $f\left(z\right)$ 为 $\left|z\right|<R\left(0<R\le +\infty \right)$ 内非常数亚纯函数。又设 $a_j\left(j=1,2,\cdots ,q\right)$ 为 $q\left(\ge 3\right)$ 个互不相同的复数(有穷或者无穷)。若 $f\left(0\right)\ne 0,\infty ,a_j\left(j=1,2,\cdots ,q\right)$ 及 $f^{\prime }\left(0\right)\ne 0$ ，则

$\left(q-2\right)T\left(r,f\right)\le {\displaystyle \underset{j=1}{\overset{q}{\sum }}N}\left(r,\frac{1}{f-a_j}\right)-N_1\left(r\right)+S\left(r,f\right)$

其中 $S\left(r,f\right)=m\left(r,\frac{f^{\prime }}{f}\right)+m\left(r,{\displaystyle \underset{j=1}{\overset{q}{\sum }}\frac{f^{\prime }}{f-a_j}}\right)+q{\log }^{+}\frac{2q}{\delta }+\log 2+\log \frac{1}{\left|f^{\prime }\left(0\right)\right|}$ ， $\delta =\underset{1\le i<j\le q}{\min }\left|a_i-a_j\right|$ ， $N_1\left(r\right)=2N\left(r,f\right)-N\left(r,f^{\prime }\right)+N\left(r,\frac{1}{f^{\prime }}\right)$ 。

注2 定理中 $S\left(r,f\right)$ 称为余项，若去掉定理中函数 $f\left(z\right)$ 在 $z=0$ 的限制，结论仍然成立，只需改变余项 $S\left(r,f\right)$ 中的常数部分。

4. 定理的证明

倘若不然，不妨假设 $\mathcal{F}$ 在点 $z_0\in D$ 处不正规。由引理3.1可得，存在点列 $\left\{z_n\right\}\subset D$ 满足 $z_n\to z_0\in D$ ，全纯曲线列 $\left\{f_n\right\}\subset \mathcal{F}$ ，正数列 $\left\{{\rho }_n\right\}\to 0^{+}$ ，使得

$g_n\left(\xi \right);=f_n\left(z_n+{\rho }_n\xi \right)\underset{F-S}{\overset{\xi \in ℂ}{\Rightarrow }}g\left(\xi \right)$ ，

其中g是 $ℂ$ 上的非常值全纯曲线。

因 $\underset{z\in D}{\min }\left|a_i\left(z\right)-a_j\left(z\right)\right|\ge \delta >0,1\le i<j\le 3$ ，故 $a_1\left(z_0\right),a_2\left(z_0\right),a_3\left(z_0\right)$ 互不相同。

假设 $\exists {\xi }_n,{\xi }_n\to {\xi }_0$ ，使 $g_n\left({\xi }_n\right)=a_i\left(z_n+{\rho }_n{\xi }_n\right)$ ，则有

$f_n\left(z_n+{\rho }_n{\xi }_n\right)=a_i\left(z_n+{\rho }_n{\xi }_n\right)$

由定理条件，有

${f^{\prime }}_n\left(z_n+{\rho }_n{\xi }_n\right)=a_i\left(z_n+{\rho }_n{\xi }_n\right)$

则

${g^{\prime }}_n\left({\xi }_n\right)={\rho }_n{f^{\prime }}_n\left(z_n+{\rho }_n{\xi }_n\right)={\rho }_n{a}_i\left(z_n+{\rho }_n{\xi }_n\right)$

令 $n\to \infty$ ， $g^{\prime }\left({\xi }_0\right)=0$ ，则 $g\left(\xi \right)$ 取 $a_i\left(z_0\right)$ 为重值， $i=1,2,3$ 。

下证：当 $a_i\left(z_0\right)\ne 0$ ， $g\left(\xi \right)\ne a_1(\; z\; 0\; )$

若不然，设其为 $m\left(\ge 2\right)$ 重零点

因为

$g_n\left({\xi }_n\right)=f_n\left(z_n+{\rho }_n{\xi }_n\right)=a_1\left(z_n+{\rho }_n{\xi }_n\right)$ ,

所以有

${f^{\prime }}_n\left(z_n+{\rho }_n{\xi }_n\right)=a_1\left(z_n+{\rho }_n{\xi }_n\right)\ne 0$

${g^{\prime }}_n\left({\xi }_n\right)={\rho }_n{f}_n\left(z_n+{\rho }_n{\xi }_n\right)={\rho }_n{a}_1\left(z_n+{\rho }_n{\xi }_n\right)$

则

${g^{\prime }}_n\left({\xi }_n\right)-{\rho }_n{a}_1\left(z_n+{\rho }_n{\xi }_n\right)=0$

记 $G_n\left(\xi \right)={g^{\prime }}_n\left(\xi \right)-{\rho }_n{a}_1\left(z_n+{\rho }_n\xi \right)$ ，令 $n\to \infty$ ，则有

$G_n\left(\xi \right)\Rightarrow g^{\prime }(\; \xi \; 0\; )$

则 ${\xi }_{nj}$ 是 $G_n\left(\xi \right)$ 的m个简单零点，矛盾。

故 $g\left(\xi \right)\ne a_1\left(z_0\right)$ 。

若 $g\left(\xi \right)-a_3\left(z_0\right)$ 的重数 $\ge 2$ ，则由引理3.3，可得

$\begin{array}{c}\left(3-2\right)T\left(r,g\right)<{\displaystyle \underset{i=1}{\overset{3}{\sum }}\bar{N}}\left(r,\frac{1}{g-a_i\left(z_0\right)}\right)+S\left(r,g\right)\\ \le {\displaystyle \underset{i=1}{\overset{3}{\sum }}\frac{1}{m_i}N}\left(r,\frac{1}{g-a_i\left(z_0\right)}\right)+S\left(r,g\right)\\ \le {\displaystyle \underset{i=1}{\overset{3}{\sum }}\frac{1}{m_i}T}\left(r,\frac{1}{g-a_i\left(z_0\right)}\right)+S\left(r,g\right)\\ \le {\displaystyle \underset{i=1}{\overset{3}{\sum }}\frac{1}{m_i}T}\left(r,g\right)+S\left(r,g\right)\\ \le \frac{1}{2}T\left(r,g\right)+S\left(r,g\right)\end{array}$

其中 $m_i$ 为 $g-a_i\left(z_0\right)$ 的重数， $m_1=m_2=\infty$ ， $m_3\ge 2$ 即

$T\left(r,g\right)\le \frac{1}{2}T\left(r,g\right)+S\left(r,g\right)$ ，矛盾。

故 $g\left(\xi \right)$ 不取 $a_3\left(z_0\right)$ 为重值

则 $\mathcal{F}$ 在D上正规。

致谢

作者衷心感谢刘晓俊老师的指导和建议。

文章引用

王 瑶. 涉及分担小函数正规定则的研究
Research on the Normal Rule of Sharing Small Functions[J]. 理论数学, 2023, 13(04): 881-885. https://doi.org/10.12677/PM.2023.134093

参考文献