Pure Mathematics
Vol.
13
No.
08
(
2023
), Article ID:
70610
,
8
pages
10.12677/PM.2023.138242
一阶、二阶常微分方程简捷解法
晏建学1,张曦丹2,朱南丽1
1云南财经大学商学院,云南 昆明
2云南财经大学物流与管理工程学院,云南 昆明
收稿日期:2023年7月6日;录用日期:2023年8月7日;发布日期:2023年8月14日

摘要
本文针对一阶、二阶可降阶、二阶常系数线性常微分方程的常规解法进行梳理,对题型加以细化,并针对每一种细化题型总结出一套较为独特简捷的解法。创新之处在于针对一阶线性微分方程三种题型直接凑微分,二阶可降阶微分方程不设中间变量直接凑微分,二阶常系数线性常微分方程三种题型(特征方程单根、二重根、共轭复根)直接凑微分求通解,二阶常系数非齐次线性微分方程三种基本题型及四种扩展题型直接求特解,解题方法快速简洁,深受学生好评。
关键词
凑微分,
凑,
凑,齐次,非齐次,多项式,指数函数,三角函数,通解,特解

Solving Process Simply for First-Order and Second-Order Ordinary Differential Equation
Jianxue Yan1, Xidan Zhang2, Nanli Zhu1
1Business School, Yunnan University of Finance and Economics, Kunming Yunnan
2School of Logistics and Management Engineering, Yunnan University of Finance and Economics, Kunming Yunnan
Received: Jul. 6th, 2023; accepted: Aug. 7th, 2023; published: Aug. 14th, 2023

ABSTRACT
This paper combs the conventional solving process for first-order, second-order reducible, second-order constant coefficient linear ordinary differential equation, refines the types of problems, and summarizes a set of unique and simple solving process for each refined type of problems. The innovation lies in the direct integration of three types of problems of the first order linear differential equation, the second order reducible differential equation without intermediate variables, the second order constant coefficient linear ordinary differential equation with three types of problems (single root, double root and conjugate complex root of characteristic equation), the second order constant coefficient linear non-homogeneous differential equation with three basic problems and four extended problems, and the direct integration of differential equations to find general solutions. The solution method is fast and simple, and praised by students highly.
Keywords:Piecemeal Differential, Piecemeal
, Piecemeal
, Homogeneous, Non-Homogeneous, Polynomial, Exponential Function, Trigonometric Functions, General Solution, Special Solution

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 微分方程基本概念
含未知函数及其导数的方程称为微分方程 [1] ,微分方程广泛应用于物理、工程、经济等多个领域描述众多实际现象和问题。微分方程分为许多不同类型,每种类型都有自己独特的性质和解法,解题方法灵活多变,难以掌握。笔者在多年教学中针对一阶、二阶可降阶、二阶常系数常微分方程常规解法进行梳理,对题型进行细化,针对一阶线性微分方程三种题型直接凑微分,二阶可降阶微分方程不设中间变量直接凑微分,二阶常系数线性常微分方程三种题型(特征方程单根、二重根、共轭复根)直接凑微分求通解 [2] ,二阶常系数非齐次线性微分方程三种基本题型及四种扩展题型直接求特解,解法独特简捷,深受学生好评。
常见的微分方程类型如下 [3] :
1) 可分离变量微分方程
2) 齐次(可化为齐次)微分方程
3) 一阶线性微分方程
Bernulli方程
4) 可降阶高阶微分方程
、
、
5) 二阶常系数齐次线性、非齐次线性微分方程
,
本文例题及常规解法出自同济大学数学系《高等数学》(第七版)上册 [1] (高等教育出版社2014年北京)。
2. 可分离变量的微分方程
两边积分:
,得到
例1:
,
,
,
,
3. 齐次方程
令
,则
,
,
,
,化为可分离变量微分方程,两边积分:
,得到
例2:
,
,
,
,
两边积分:
,
。
4. 一阶线性微分方程
三种题型及其解法:将
凑一块,然后积分
1) 题型一:
两边积分:
例3:
,
,
2) 题型二:
,
,积分
例4:
,
,
,
,
3) 题型三:
,
积分:
,求出
例5:
,
,
,
。
5. 可降阶二阶微分方程三种题型及其解法
1) 题型一:
——逐次积分法
例6:
,积分三次,得到
,
,
2) 题型二:
——凑微分法,凑
(无需令
),然后分离变量,再积分
例7:
,
,
,
,
,
,
3) 题型三:
——凑微分法,将
凑一块,
凑一块(无需令
)再求解
例8:
,
,
,
,
令
,
,
,
,
,
,
,
,
例9:
,
,
,
,
,
,
,
,
,
,
。
6. 二阶常系数齐次线性微分方程
的通解
该常规方法用于求齐次的通解,便于记忆,方便实用(表1)。

Table 1. General solution of second order homogeneous linear differential equation with constant coefficients y ″ + p y ′ + q y = 0 (from the first volume of the seventh edition of Advanced Mathematics, Tongji University) [1]
表1. 二阶常系数齐次线性微分方程
的通解(出自同济大学《高等数学》第七版上册) [1]
7. 二阶常系数非齐次线性微分方程
的特解
用待定系数法求非齐次的特解比较繁琐,需同时考虑左边的特征方程单根、二重根、共轭复根及右端的非齐次项与特征方程根的关系。当特征方程有重根且方程右边
中
是特征方程的单根、是特征方程的二重根时求解过程就更加繁琐,尤其是特征方程有共轭复根且方程右边带三角函数时求解之繁琐更让人苦不堪言 [1] [3] (表2)。

Table 2. Special solution of second order non-homogeneous linear differential equation with constant coefficients y ″ + p y ′ + q y = f ( x ) (from the first volume of the seventh edition of Advanced Mathematics, Tongji University) [1]
表2. 二阶常系数非齐次线性微分方程
的特解(出自同济大学《高等数学》第七版上册) [1]
笔者对该常规解法加以改进,对题型加以细化,并针对每一种细化题型总结出独特简捷的解法 [2] 。
8. 二阶常系数非齐次线性微分方程
求通解方法——凑微分并 积分两次,该方法只需对方程左边凑微分而无需考虑方程右端非齐次项
1) 题型一:
型,特征方程
有两个不相等实根
 ,
,
,
,
 ,
,
,
,
例10:
,
,
,
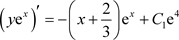 ,
,
,
,
例11:
,
,
,
,
,
,
2) 题型二:
型,特征方程
有两个相等实根
,速解
,
,
例12:
,
,
,
3) 题型三:
型,特征方程
有一对共轭复根
,
,
,
,
,
用欧拉公式
,
,
,
针对
型求解 [1] ,
解为
,而
解为
,则
例13:
,
 ,
,
,
,
例14:
,
,
设
,
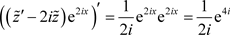 ,
,
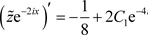 ,
,
,
,
,
,
。
9. 二阶常系数非齐次线性微分方程
求特解——3种基本题型、 4种扩展题型,该方法只需考虑方程右端非齐次项
的类型,解题思路清晰, 步骤简捷
1) 基本题型一:
多项式型,特解
与
次数相同
例15:
,
特解
满足
,
,
例16:
,特解
满足
,
2) 基本题型二:
指数函数型,特解
与
同型
例17:
,
例18:
,设
,
特解
满足
,
,
,
3) 基本题型三:
型——特解
与
同型
例19:
,
讨论:
及共轭微分方程:
设
,
,
,特解
例20:
,
讨论:
及共轭微分方程:
设
,
,
,
,
,
特解
4) 扩展题型一:
指数函数乘多项式型,特解
与
同型
例21:
,设
,
,
,
特解
,
,
通解
5) 扩展题型二: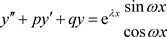 指数函数乘三角函数型,特解
与
同型
指数函数乘三角函数型,特解
与
同型
例22:
,设
,则
,
,
,
,
,
6) 扩展题型三:
多项式乘三角函数型,特解
与
同型
例23:
讨论
及共轭方程
,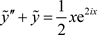
设
,则
,
,
7) 扩展题型四:
指数函数多项式三角函数乘积型,特解
与
同型
例24:
,
,
,设
,
则
,
,
。
基金项目
云南财经大学科学研究基金项目。
文章引用
晏建学,张曦丹,朱南丽. 一阶、二阶常微分方程简捷解法
Solving Process Simply for First-Order and Second-Order Ordinary Differential Equation[J]. 理论数学, 2023, 13(08): 2345-2352. https://doi.org/10.12677/PM.2023.138242
参考文献
- 1. 同济大学数学系, 编. 高等数学(上册) [M]. 第7版. 北京: 高等教育出版社, 2014: 297-354.
- 2. 晏建学. 微积分、线性代数、概率论与数理统计解题指导及提高[M]. 昆明: 云南科技出版社, 2018.
- 3. 马锐, 主编. 高等数学[M]. 第2版. 北京: 高等教育出版社, 2019.






 ,
,
,
, ,
,
,
,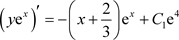 ,
,
,
,
 ,
,
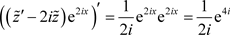 ,
,
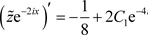 ,
,
,
,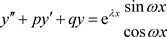 指数函数乘三角函数型,特解
与
同型
指数函数乘三角函数型,特解
与
同型