Computer Science and Application
Vol.
10
No.
01
(
2020
), Article ID:
34048
,
13
pages
10.12677/CSA.2020.101016
Prediction of Soluble Zinc Rate during Roasting Process Based on Particle Swarm Optimization in Deep Belief Network
Hongchuan Yang, Yonggang Li
School of Automation, Central South University, Changsha Hunan
Received: Jan. 2nd, 2020; accepted: Jan. 13th, 2020; published: Jan. 20th, 2020

ABSTRACT
In order to solve the problem that the soluble zinc ratio is difficult to be measured online in the roasting quality of zinc smelting and roasting process, a Deep Belief Network (DBN) algorithm was proposed to predict the soluble zinc rate. However, the DBN network structure is an important factor affecting its prediction performance, and it is difficult to determine the appropriate network structure. It is proposed to use the information entropy method to determine the appropriate number of hidden layer, then use the PSO algorithm to optimize the number of hidden layer nodes and learning rate, and finally determine the DBN network structure. The method was validated by data set simulation and practical application of soluble zinc rate prediction, and compared with BP neural network and RBF neural network models. The results show that the DBN network structure optimized by the information entropy method and the PSO algorithm has higher prediction accuracy and stronger fitting ability.
Keywords:Deep Belief Network, Information Entropy, Network Structure, Particle Swarm Optimization, Soluble Zinc Rate

基于粒子群算法的深度置信网络焙烧过程可溶锌率预测
杨红川,李勇刚
中南大学自动化学院,湖南 长沙

收稿日期:20120年1月2日;录用日期:2020年1月13日;发布日期:2020年1月20日

摘 要
针对锌冶炼焙烧过程焙砂质量衡量指标可溶锌率难以在线测量的问题,提出采用深度置信网络算法(Deep Belief Network, DBN)预测可溶锌率。但DBN网络结构是影响其预测性能的重要因素,合适的网路结构又难以确定,故提出先用信息熵法确定合适的隐层层数,再用PSO算法对隐层节点数和学习率进行优化,最终确定DBN网路结构。通过数据集仿真和可溶锌率预测实际应用,对该方法进行验证,与BP神经网络、RBF神经网络预测模型进行对比。结果表明,用信息熵法和PSO算法优化确定的DBN网络结构,预测精度更高,拟合能力更强。
关键词 :深度置信网络,网络结构,信息熵,粒子群算法,可溶锌率

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
焙烧过程是锌冶炼的重要工序之一,锌精矿经过焙烧之后,得到浸出原料锌焙砂,焙砂的可溶锌率直接影响后续工序能否正常进行。焙烧温度、焙烧时间、风料比等焙烧操作条件直接关系到锌焙砂的质量,对可溶锌率有重要影响。因此实现锌焙砂可溶锌率的准确预测不仅对锌焙砂质量的提高有重要意义,而且可通过预测结果及时调整焙烧过程工艺参数实现沸腾焙烧炉的稳定控制,保证整个湿法炼锌流程操作的正常运行。
人工神经网络模拟的是大脑工作方式,在机器学习(ML)和人工智能(AI)等领域有着举足轻重的地位。Hinton教授提出的深度置信网络(DBN) [1] [2] [3],提高了人类在神经网络多隐含层领域的认知。目前在许多领域都有DBN的成功应用 [4] - [16],尽管DBN在很多领域一定程度上取得了成功的应用,但关于锌冶炼焙烧过程可溶锌率预测应用的文献报道很少。许冬 [17] 运用BP神经网络算法,通过物料组成、操作条件作为输入,可溶锌率作为输出建立的预测模型,虽然能较为准确地预测可溶锌率,但BP神经网络算法属于浅层算法,在有限的样本数量下难以有效地表示非线性复杂函数,泛化能力受到限制,进而影响预测的可靠性,故其准确率有待提高。故采用DBN的方法准确预测焙砂可溶锌率具有相当大的实用性和挑战性。
DBN网络的特点是通过深层次的网络结构,逐层学习训练的方式提高对复杂非线性函数拟合能力,进而提高模型的性能。因此要确定一个合适的网络结构。在实际的应用中,没有成熟的理论帮助确定网络结构,一般是依据积累的经验,多次实验去选择合适的网络结构。Shen [18] 通过人工反复试验确定的DBN网络结构,但其确定的网络结构复杂且不合理,造成DBN模型运行时间长,模型性能较差。因此,如何优化出最适合的网络结构,对DBN在人工智能领域的应用研究,具有重要的意义。针对这个问题,首先通过信息熵法确定隐层层数,然后采用PSO算法对DBN网络结构的神经元个数和学习率进行优化,确定一个合适的DBN网路结构。这样能够避免模型结构参数选择的盲目性,减少其对模型精度的影响。
2. DBN预测模型
DBN是根据生物神经网络的研究及浅层神经网络发展而来的,为概率生成模型,通过联合概率分布推断出数据样本分析。DBN生成模型通过训练网络结构中的神经元间的权重使得整个神经元网络依据最大概率生成训练数据,形成高层抽象特征,提升模型性能。
2.1. 深度置信网络
深度学习的常见框架之一是DBN,它是由多个限制玻尔慈曼机(RBM)层组成。其运用分层次抽象的概念,通过分层结构,使用Hinton提出的贪婪算法自下而上的逐层无监督学习,再由自上而下的有监督学习来微调整个网络结构的权值,从而选取数据中更有效的特征。
RBM由两层组成,如图1所示。

Figure 1. RBM network structure
图1. RBM网络结构
每一层的节点之间没有链接。一层是可视层,即数据输入层,一层是隐藏层,其所有的节点都是随机二值变量节点(只能取0或者1值)。假设可视层为v,隐藏层为h,它们的单元数目分别为m、n,则联合组态的能量可表示为:
(2.1)
其中: 是RBM的参数; 是可视层单元i与隐藏层单元j之间的连接权值; 、 分别表示可视层单元和隐藏层单元的偏置。通过Bolizmann分布和式(1)可以确定这个组态的联合概率分布:
(2.2)
(2.3)
其中: 为归一化因子,在实际问题中,通常较多的关注联合概率分布 的边缘分布。由此,可以得出v的分布 ,即联合概率分布 的边缘分布为:
(2.4)
由RBM网络的结构性质可知,各可视层单元或隐藏层单元的激活状态之间不存在任何联系,也就是说各层神经元之间是相互独立的。因此,由(2)式的联合概率分布可知,当输入参数与可视层向量v已知时,可得隐藏层h的概率如式(5)所式,当输入参数与隐藏层向量h已知时,可得出可视层v的概率如式(6)所式:
(2.5)
(2.6)
因此,当隐藏层状态已知时,第i个可视层神经单元被激活的概率如式(2.7),当可视层状态已知时,第j个隐藏层神经单元的被激活的概率分布如式(2.8):
(2.7)
(2.8)
其中: 为sigmoid函数。
DBN使用无监督贪婪算法自下而上的逐层训练学习产生各层之间的权值。训练过程中,首先可视层单元映射到隐藏层单元,隐藏层单元再反射过来重构可视层单元,反复执行这个步骤得到权值。每一层RBM隐藏层的输出作为下一层RBM可视层的输入。与传统神经网络的算法不同的是,DBN的训练只需要单个步骤就能实现最大程度的函数逼近,训练时间明显减少。在上面的预训练过程结束后,DBN使用有标签数据通过BP算法有监督的反向传播来微调预训练生成的权值,得到较为精确的预测模型。DBN网络结构如图2所示。

Figure 2. Structure of DBN network prediction model
图2. DBN网络预测模型结构
2.2. 数据集选择及评价指标
为了充分验证DBN预测模型的性能,并为后续算法的应用提供指导,用糖尿病预测数据,分析和验证DBN预测模型以及采用PSO优化后的DBN预测模型。该数据从Kaggle Datasets数据库获得,该库使用范围广,颇受研究者的认可。该数据共1000组,9列,随机把数据集分为950组训练集和50组测试集。
为了说明模型预测效果,本文选用常用的均方误差(Mean squared error, MSE)、决定系数(Coefficient of determination) R²和平均绝对百分比误差(Mean absolute percentage error, MAPE)来检验和衡量模型的精确度和效果的指标。MSE、R²和MAPE定义如下:
(2.9)
(2.10)
(2.11)
式中:
为实际值,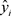 为模型预测值,
为真实值的平均值,n样本数据量。
为模型预测值,
为真实值的平均值,n样本数据量。
2.3. 数据预处理
在预测模型建立之前,要考虑输入和输出数据之间数据级及量纲之间的差别,需要对训练数据进行预处理以提高预测模型的可靠性和精度。对数据做归一化处理,归一化公式为:
(2.12)
式中, 为做归一化处理后的数据序列,X为做归一化处理前的各数据序列, 为数据序列中的最大值, 为数据序列中的最小值。归一化处理一般是将数据变换到[0,1]之间。
当预测模型计算结束后,再通过反归一化得到预测数据。
3. 基于信息熵和PSO的DBN结构优化
3.1. DBN网络结构对性能的影响
DBN网络结构设计就是选择合适的隐层层数、神经元个数及网络参数来确定网络结构。在DBN网络中,如果隐层层数选择得当,模型性能可以明显的提高。通过增加隐层层数不仅可以降低模型的重构误差,而且能挖掘出数据中更为抽象的特征信息,由于隐层层数的增加网络结构通常会更加复杂,若隐层层数过少,模型的学习能力不足,不能较好的解决实际问题。因此,要选取合适的隐层层数。
隐层神经元个数的选择对DBN模型的性能影响也较大,其个数无论过多还是过少都会对模型的性能有明显的影响。若DBN模型的隐层神经元个数过少,不但学习能力而且信息处理能力都会显著降低,数据的特征信息提取能力也会大打折扣。反之,若隐层神经元个数过多,降低网络的重构误差能力可能会明显的提高,但网络会容易陷入局部极小值,没有最优解,同时模型的学习速度也会变慢,随之模型的泛化能力也会降低 [19]。直到现在仍没有一种科学和普遍的方法设定DBN隐层神经元个数,通常依靠经验进行设定。
学习率(Learn Rate)是DBN网络的重要参数之一,网络的循环训练过程中权重变化量由它决定。若设定的学习率较大,可能会导致权重变化较大,影响模型的稳定性;若设定的学习率较小,模型的训练时间会增加,且收敛速度会更慢。因此,无论学习率过大还是过小对DBN模型性能的影响都是显著的。对于学习率的设定大多需要多次调解或基于前人经验。
3.2. 基于信息熵确定DBN网络隐层层数
信息熵是科学家香农为描述一个系统所含信息的大小而定义的,即信息熵是信息的一个度量。故信息熵可以说是系统信息量大小的一个度量。采用信息熵的方法来确定网络的最佳层数,当DBN网络训练达到稳定程度后通过计算各隐含层信息熵来判断最佳层数,该层信息熵的值达到最大,则为最佳隐层层数。
假设一个系统的信息熵H(x)可以定义为:
(3.1)
式中: 且 ,当 时,规定 。
利用拉格朗日乘数构造法构造函数:
(3.2)
令 ,,可以得到:
(3.3)
(3.4)
由于 ,可以得到:
(3.5)
由此得知:
(3.6)
当信息熵最大时:
将 代入式(19)得:
(3.7)
假设一个构建好的输入层与隐层之间的权重用矩阵W表示,且:
相邻两层之间的偏置用a表示,且: 即上一层的输出作为下一层的输入表示:
(3.8)
其中: 和 表示相应层的第i,j个单元值,b为相邻两层间的连接权值。
假设某DBN的隐层神经元数为m,隐层数为n,且DBN网络每层神经元数可代表该层信息量,故可得出神经元数与隐层信息量之比为:
(3.9)
在同一个DBN网络中,信息熵可度量每层信息量的大小。即:
(3.10)
由式(22)和(23)得:
(3.11)
首先固定隐层神经元个数,然后进行仿真实验得到不同隐含层的信息熵如图3所示以及不同隐层层数下DBN预测性能如表1所示:

Figure 3. Information entropy of different hidden layer Numbers
图3. 不同隐层层数的信息熵
Table 1. Performance prediction of DBN model under different hidden layers
表1. 不同隐层层数下DBN模型预测性能
从图3和表1可以看出当隐层层数为3时,信息熵值达到最大,DBN模型评价指标MSE、MAPE、R²优于其它层数,因此选择3层作为最佳隐层层数。运用信息熵法确定合适的隐层层数,不仅可以使整个DBN预测模型能更好地提取输入数据的特征,而且有效的避免欠拟合和过拟合现象的发生,防止陷入局部最优值,使模型的重构误差最小,提高网络的学习效率和精度。
3.3. 基于PSO-DBN网络结构优化方法
3.3.1. 粒子群算法
PSO算法中,搜索空间上的每一个点都可以被想象成待优化问题的潜在解,这个点称之为“粒子”(Particle),任何粒子都有一个被目标函数所决定的适应值,并且粒子移动的方向和距离都会有一个速度决定,然后粒子们就追随当前最优粒子在解空间搜索。其中粒子的速度和运动方向更新公式如下:
(3.12)
(3.13)
其中 代表第i个粒子的速度,w代表惯性权值, 和 表示学习参数, 表示在0~1之间的随机数, 代表第i个粒子搜索到的最优值,gbest代表整个集群搜索到的最优值, 代表第i个粒子的当前位置。
3.3.2. PSO-DBN模型训练过程
PSO算法流程:
Input:种群规模m,惯性权重w,加速常数c1,c2,最大速度Vmax,最大迭代次数Gmax。
Output:DBN网络待优化参数。
1:初始化一群粒子 (规模为m),随机初始化它们的位置和速度;
2:根据目标函数,计算每个微粒的适应度值;
3:训练DBN算法;
4:对每个粒子,将它当前的适应度值和它经历过的最好位置(pbest)的值比较,若当前较好,则将其作为新的最好位置pbest;
5:对每个粒子,将它当前的适应度值和它整个种群的最好位置(gbest)的值比较,若当前较好,则将其作为新的种群最好位置gbest;
6:按照方程(9)和(10)更新每个粒子的速度和位置;
7:判断是否达到结束条件(通常为足够好的适应值或达到最大迭代次数Gmax),不满足就返回2,若满足则输出为DBN网络模型参数。
DBN网络训练两个阶段是预训练和反向微调。
Step1:模型预训练:
预训练的过程是从下往上的,逐层无监督训练每一个RBM网络,确保在特征映射过程中特征向量映射到不同的特征空间时,充分保留特征信息。最后映射到输出层,输出激励函数为softmax函数,通过和数据标签进行对比,随机初始化输出层权值w。
Step2:权值微调:
经过Step1预训练之后,得到了网络的初始权值 。通过在DBN的最后一层设置BP网络,根据样本数据标签反向传播有监督地微调初始权值。微调过程中,使用以下目标函数:
(3.14)
其中, ,即需要微调权值, 为样本标签, 为预测结果。因为w是随机初始化,所以微调过程中需要先调整w的值,若干次迭代后,再微调 的值,直到输出误差足够小为止。
PSO-DBN训练流程如图4所示。
3.4. 仿真验证
表2是DBN预测模型优化前后参数对比表。

Figure 4. PSO-DBN network prediction model training process
图4. PSO-DBN网络预测模型训练流程
 (a) 预测图
(a) 预测图 (b) 预测误差图
(b) 预测误差图
Figure 5. Prediction results of DBN network prediction model before optimization
图5. DBN网络预测模型优化前预测结果
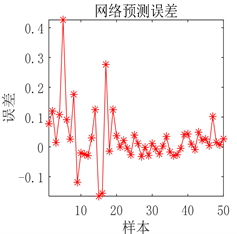 (a) 预测图
(a) 预测图 (b) 预测误差图
(b) 预测误差图
Figure 6. Prediction results of DBN network prediction model after optimization
图6. DBN网络预测模型优化后预测结果
Table 2. Experimental parameters and PSO optimization network parameters
表2. 实验参数和PSO优化网络参数
用人工通过反复试验确定的DBN预测模型从图5可以看出虽然预测误差较小,但是对于极个别的测试样本预测结果不准确。从图6可以看出采用PSO优化后的DBN预测模型,其预测误差明显降低,几乎没有预测不准确的测试样本存在,模型预测精度显著提高。
4. 应用研究
锌冶炼焙烧过程是运行复杂的工业过程,存在大量可以在线获得的过程变量,这些变量对于锌冶炼过程的控制非常重要,是锌冶炼过程中必须监测的变量。本文采用国内某大型锌冶炼厂沸腾焙烧过程的实际生产现场采集了500组数据用于验证该方法的有效性,其中的可溶锌率是由该公司技术人员通过采样到的焙砂进行化验分析得到。根据焙砂中可溶锌率影响因素变化的基本规律,经过筛选处理后,选取其中的450组,它们满足基本的焙烧理论和该公司的生产实践。例如,精矿中的锌含量增加,焙砂中的可溶锌率提高。其中前400组作为模型的训练样本,后50组作为模型的测试样本,对方法进行验证。
通过实验所得结果确定DBN模型包括一个输入层,3个隐藏层和一个输出层。输入层为锌含量、铁含量、焙烧温度、焙烧时间、风料比、烟气出口压力,输出层为焙砂的可溶锌含量。PSO算法参数设置如表3所示。
Table 3. Parameter setting of PSO algorithm
表3. PSO算法参数设置
预测结果分析
下表4是DBN实验设置参数和PSO优化之后的参数结果对比表:
Table 4. Comparison of experimental parameters and PSO optimization network parameters
表4. 实验参数和PSO优化网络参数对比
将PSO优化后的参数回带到DBN预测模型,预测结果对比如下:
 (a) 预测图
(a) 预测图 (b) 实际值与预测值拟合图
(b) 实际值与预测值拟合图
Figure 7. Prediction results of DBN network prediction model before optimization
图7. DBN网络预测模型优化前预测结果
 (a) 预测图
(a) 预测图  (b) 实际值与预测值拟合图
(b) 实际值与预测值拟合图
Figure 8. Prediction results of DBN network prediction model after optimization
图8. DBN网络预测模型优化后预测结果
DBN模型参数优化前后评价结果量化如表5所示:
Table 5. Comparison of DBN model experimental parameters and PSO optimization parameters prediction and evaluation
表5. DBN模型实验参数与PSO优化参数预测评价对比
从图6、图7、图8和表5的结果可以看出,使用PSO算法优化得出的DBN网络参数之后,模型的预测值与真实值之间的误差更小,拟合的更好。决定系数R²更接近于1,证明模型的拟合效果更好,预测能力更强。说明优化模型参数比经验模型参数的预测性能更好,可以得出用PSO算法优化DBN网络模型结构是一种行之有效的方法。
为充分验证本文所采用的预测模型的有效性及科学性,选取BP神经网络预测模型和RBF神经网络预测模型浅层神经网络进行比较分析。
 (a) 预测图
(a) 预测图  (b) 实际值与预测值拟合图
(b) 实际值与预测值拟合图
Figure 9. Prediction results of BP neural network prediction model
图9. BP神经网络预测模型预测结果
 (a) 预测图
(a) 预测图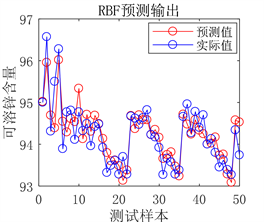 (b) 实际值与预测值拟合图
(b) 实际值与预测值拟合图
Figure 10. Prediction results of RBF neural network prediction model
图10. RBF神经网络预测模型预测结果
Table 6. Comparison of performance indexes of soluble zinc rate prediction model
表6. 可溶锌率预测模型性能指标对比表
从图9、图10及表6可以看出,BP和RBF神经网络预测模型预测结果虽然可以与实际值基本拟合,但误差相对于DBN预测模型较大,决定系数R²值较小,证明BP和RBF预测模型的拟合能力较弱,相较于DBN模型预测性能较差,在面对复杂情况时,并不能很好的满足实际生产应用。
5. 结束语
本文针对锌冶炼焙烧过程焙砂质量指标可溶锌率测量存在的问题,提出采用深度置信网络(DBN)预测可溶锌率,但DBN网络结构对模型性能有很大的影响且其结构难以确定。针对DBN网络结构难以确定的问题,提出采用信息熵法确定隐层层数,运用粒子群算法对隐层神经元个数和学习率进行优化。本文通过数据集实验仿真以及工业实际应用研究证明,采用PSO算法优化DBN网络结构不仅可以节约大量花费在确定网络结构的时间,而且有效地提高了DBN预测模型的精度。证明了该方法的可靠性和可行性,可用于实际工业生产中。
基金项目
国家自然科学基金(61890930-2)。
文章引用
杨红川,李勇刚. 基于粒子群算法的深度置信网络焙烧过程可溶锌率预测
Prediction of Soluble Zinc Rate during Roasting Process Based on Particle Swarm Optimization in Deep Belief Network[J]. 计算机科学与应用, 2020, 10(01): 141-153. https://doi.org/10.12677/CSA.2020.101016
参考文献
- 1. Lee, T.S. and Mumford, D. (2003) Hierarchical Bayesian Inference in the Visual Cortex. Journal of the Optical Society of America, 20, 1434-1448.
- 2. 潘广源, 柴伟, 乔俊飞. DBN网络的深度确定方法[J]. 控制与决策, 2015, 30(2): 256-260.
- 3. Hinton, G.E. and Salakhutdinov, R.R. (2006) Reducing the Dimensionality of Data with Neural Net-works. Science, 313, 504-507. https://doi.org/10.1126/science.1127647
- 4. Dahl, G.E., Yu, D., Deng, L. and Ac-ero, A. (2011) Large Vocabulary Continuous Speech Recognition with Context-Dependent DBN-HMMS. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP 2011, Prague Congress Center, Prague, 22-27 May 2011, 4688-4691. https://doi.org/10.1109/ICASSP.2011.5947401
- 5. 徐春华, 陈克绪, 马建, 刘佳翰, 吴建华. 基于深度置信网络的电力负荷识别[J]. 电工技术学报, 2019, 34(19): 4135-4142.
- 6. 毛勇华, 代兆胜, 桂小林. 一种改进的5层深度学习结构与优化方法[J]. 计算机工程, 2018, 44(6): 147-150.
- 7. Wang, Y.B., You, Z.H., Li, X., et al. (2017) Predicting Protein-Protein Interactions from Protein Sequences by a Stacked Sparse Autoencoder Deep Neural Network. Molecular Biosystems, 13, 1336-1344. https://doi.org/10.1039/C7MB00188F
- 8. Liu, F., Jiao, L.C., Hou, B. and Yang, S.Y. (2016) POL-SAR Image Classification Based on Wishart DBN and Local Spatial Information. IEEE Transactions on Geoscience & Remote Sens-ing, 54, 1-17. https://doi.org/10.1109/TGRS.2016.2514504
- 9. Kong, W., Zhao, Y.D., Hill, D.J., Luo, F. and Xu, Y. (2018) Short-Term Residential Load Forecasting Based on Resident Behaviour Learning. IEEE Transactions on Power Systems, 33, 1087-1088. https://doi.org/10.1109/TPWRS.2017.2688178
- 10. Li, B.-Q., He, Y.-Y., Guo, Y.-S. and Qiu, Y. (2017) Auto-matic Interpretation Algorithm for Tunnel Geological Prediction Based on DBN. Journal of Chang’an University (Natu-ral Science Edition), 37, 90-96.
- 11. 高月, 宿翀, 李宏光. 一类基于非线性PCA和深度置信网络的混合分类器及其在PM2.5浓度预测和影响因素诊断中的应用[J]. 自动化学报, 2018, 44(2): 318-329.
- 12. Zhou, S.Z.S., Chen, Q.C.Q. and Wang, X.W.X. (2010) Discriminative Deep Belief Networks for Image Classification. 2010 IEEE Interna-tional Conference on Image Processing, Hong Kong, 26-29 September 2010, 1561-1564. https://doi.org/10.1109/ICIP.2010.5649922
- 13. 张媛媛, 霍静, 杨婉琪, 等. 深度信念网络的二代身份证异构人脸核实算法[J]. 智能系统学报, 2015, 10(2): 193-200.
- 14. 朱乔木, 党杰, 陈金富, 徐友平, 李银红, 段献忠. 基于深度置信网络的电力系统暂态稳定评估方法[J]. 中国电机工程学报, 2018, 38(3): 735-743.
- 15. 张楠, 丁世飞, 张健, 赵星宇. 基于噪声数据与干净数据的深度置信网络[J]. 软件学报, 2019, 30(11): 3326-3339.
- 16. Lv, Y., Duan, Y., Kang, W., Li, Z. and Wang, F.-Y. (2015) Traffic Flow Prediction With Big Data: A Deep Learning Ap-proach. IEEE Transactions on Intelligent Transportation Systems, 16, 865-873.
- 17. 许冬. 复杂锌精矿沸腾焙烧预测神经网络研究[D]: [硕士学位论文]. 西安: 西安建筑科技大学, 2008.
- 18. Shen, F., Chao, J. and Zhao, J. (2015) Forecasting Exchange Rate Using Deep Belief Networks and Conjugate Gradient Method. Neurocomputing, 167, 243-253. https://doi.org/10.1016/j.neucom.2015.04.071
- 19. 张国辉. 基于深度置信网络的时间序列预测方法及其应用研究[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2017.
