Modeling and Simulation
Vol.
11
No.
05
(
2022
), Article ID:
56375
,
11
pages
10.12677/MOS.2022.115128
铝板焊接过程中温度场的有限元模拟
申 强,李彦业
太原科技大学应用科学学院,山西 太原
收稿日期:2022年8月29日;录用日期:2022年9月20日;发布日期:2022年9月28日

摘要
铝制结构广泛应用于车辆、航空等多个领域,焊接技术在铝制品应用过程中发挥着重要作用,准确预测铝制品在焊接过程中温度场分布和变化规律,对焊接理论以及工程实际具有重要的指导意义。本文基于COMSOL软件,模拟了300 mm * 150 mm * 8 mm的I型坡口的铝板焊件的焊接过程,主要讨论高斯热源、双椭球热源和组合热源模型下,焊接温度场分布和变化规律。研究发现,随着热源模型的改进,焊缝区域的温度场逐渐增大;在双椭球热源模型下,随着形状参数的增大,研究区域内的温度逐渐减小;在组合热源模型下,随着焊接参数的增大,焊缝区域内的温度场逐渐减小。本文得出的结论对焊接工艺的改进具有指导意义。
关键词
铝板焊接,有限元模拟,焊接参数,温度场

Finite Element Simulation of Temperature Field during Aluminum Plate Welding
Qiang Shen, Yanye Li
College of Applied Science, Taiyuan University of Science and Technology, Taiyuan Shanxi
Received: Aug. 29th, 2022; accepted: Sep. 20th, 2022; published: Sep. 28th, 2022

ABSTRACT
Aluminum structure is widely used in many fields such as vehicles and aviation. Welding technology plays an important role in the application of aluminum products. Accurately predicting the distribution and variation of temperature field of aluminum products in the welding process has important guiding significance for welding theory and engineering practice. Based on COMSOL software, this paper simulates the welding process of 300 mm * 150 mm * 8 mm type I groove aluminum plate welding parts, mainly discusses the distribution and variation of temperature field under Gauss heat source, double ellipsoid heat source and combined heat source model. It is found that with the improvement of heat source model, the temperature field of weld zone increases gradually. In the double ellipsoid heat source model, with the increase of shape parameters, the temperature in the study area will gradually decrease. In the combined heat source model, with the increase of welding parameters, the temperature field in the weld zone gradually decreases. The conclusions drawn in this paper have certain guiding significance to the improvement of welding process.
Keywords:Aluminum Plate Welding, Finite Element Simulation, Welding Parameters, Temperature Field

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
由于铝具有良好的抗氧化性,且有良好的延展性以及质量轻的特点,广泛地应用于车辆、容器制造、航空等诸多领域,其中包括铝的焊接技术。然而由于自身的材料属性对铝的焊接方式有特殊的要求 [1],随着生产制造中铝产品的结构变化以及需求的增大,铝材的焊接技术也逐渐得到优化。常见的铝焊接方法有电阻焊、摩擦焊、气保焊、激光焊等,主要原理是集中的高温热源在焊缝区域形成熔池,等到冷却后凝固焊接成型。然而不同的焊接工艺会对材料的焊接质量产生影响,因此研究铝材焊接的热力学性能,了解铝材焊接过程中温度场和应力场在不同物理参数下的变化,在实际应用问题中,对保证焊接质量具有重要的指导意义。焊接会导致材料在焊缝区域发生熔化凝固,在热影响区域会产生组织变形等现象,当受到外在约束后,会产生应力,即热应力。所以研究焊件的应力场之前先要研究材料的温度场变化。由于焊接的传热是瞬态非线性问题,所以比较复杂,冀伟等人 [2] 采用数值模拟计算了薄板焊接准稳态热传导问题的线性分析,后期验证发现他们引入的热焓和表面双椭球热源模型大大提高了模拟的准确度。随着现代科学技术的提高,国内外广大学者,将焊接从二维推向三维。庄其仁研究激光焊接的温度场,根据激光波长和金属表面穿透金属表面的直接穿透原理,导出了以高斯热源为模型的三维解析式 [3]。随后蔡志鹏以高斯热源模型先后提出分段移动热源模型和串热源模型,对于串热源模型,只需要说明节点上的输入功率和输入时间,这摆脱了节点所在面的形状的约束 [4] [5]。王能庆等人 [6] 基于双椭球热源模型建立了焊接三维温度场有限元分析模型,同时修正了模型参数,使得计算更加精确简便。程久欢等人 [7] 对焊接热源进行了综述性报道,分析了不同热源模型的特点及其优缺点。姚相林等人 [8] 采用生死单元法模拟了焊接热源的移动和材料的填充,分析了焊接过程中的温度场和应力场。李陈峰等人 [9] 采用双椭球热源模拟热输入,并通过生死单元法模拟焊料填充,较精确地模拟了铝合金焊接过程的温度场和应力场。周文静等人 [10] 应用COMSOL建立了铝合金搅拌摩擦焊的有限元模型,分析了焊速、转速变化对温度场影响。然而在焊接过程中热源的选取,是准确预测温度场的前提,因此本文基于热传导理论,采用有限元方法对300 mm * 150 mm * 8 mm的铝板进行焊接过程模拟,分析不同热源模型下焊件的温度场分布规律,并考虑了热源参数对温度场分布的影响,为焊接工艺的优化提供指导价值。
2. 焊接温度场的控制方程
焊接热传导会在铝板焊件和热源之间,以及铝板焊件内部发生,而且在一定的温度差情况下,热会从高温瞬时等温面扩散到低温瞬时等温面。同时焊接的热传导是瞬态的热传导问题,这就要求要有合理的三维瞬态热传导控制方程。物体内各点的温度会随着位置的不同和时间的变化而发生变化,因此温度T是位置坐标和时间t的函数:
(2-1)
在某个区域Ω内,都要满足如下的热传导微分方程(考虑铝板为各项同性材料):
(2-2)
式中:ρ为材料密度,c为比热容,a为导热系数,W为热源。
为了能够求解热传导微分方程,从而求出温度场,必须要明确初瞬时的温度分布,即初始条件,在本文中已经规定焊接温度场材料温度为25℃;另外还要明确初瞬时以后物体表面和周围介质之间的热交换规律,也就是边界条件。
温度场的边界条件可能有如下三种:
1、已知物体表面的任意位置的瞬时温度
(2-3)
Ts是关于坐标和时间的函数。
2、已知物体表面任意位置的热流密度
(2-4)
式中,qs为物体表面的热流密度。
3、已知物体边界上任意位置的对流放热情况
(2-5)
式中,β为表面传热系数,Te为周围介质的温度。
当边界与外界无交换时,即绝热条件下:
(2-6)
3. 焊接温度场的有限元建模
3.1. 热源模型选择
热源模型的选取是焊接数值模拟实现的前提条件,而焊接热源的主要特征包括:瞬时、快速、高温、集中,在多种参数的影响下,合理的热源模型可以得到较为精确的数值模拟,常见的热源模型包括:高斯分布热源模型、双椭球热源模型和多种热源模型的组合形式。
3.1.1. 高斯分布热源模型
焊接时将热能传递给焊件,在一定范围内形成加热面积,在一定的加热面积内热流密度的分布近似于高斯分布,所以这一热源模型称为高斯热源模型。其函数为:
(3-1)
式中 为r处的表面热流, 为热源中心热流最大值, 为热流分布集中系数。
对移动热源,其总的热量:
(3-2)
由上式可知:
(3-3)
式中q为焊接输入, 为加热面积半径,令 。
在初始固定笛卡尔坐标系中,焊接激光沿着X轴以 匀速运动,在任意坐标坐标系中,即任意面的位置上,移动坐标系为 。由上述可知,移动坐标系中距离加热面积中心的距离是
(3-4)
高斯热源模型的焊接过程中,加热焊接材料的有效功率为:
(3-5)
式中, 为焊接热效率,U为焊接电压,I为焊接电流。
综上所述
(3-6)
由(3-6)可知,这种热源模型基于二维(x-y)平面进行运算,在低速情况下有较大的误差。
3.1.2. 双椭球热源模型
高斯热源模型是在焊接表面的热源,但在实际的焊接过程中还有激光穿透的作用,在热源模型的建立中,由串热源模型演变为半球状热源分布模型,再到椭球型热源分布模型,直到现在应用更加广泛精确的双椭球热源模型。椭球内热流密度的高斯分布的函数:
(3-7)
其中 、 、 得
(3-8)
通过坐标变化得前半部分椭球内热源分布
(3-9)
当把热源分为前后两部分,前面为1/4椭球,后面是1/4椭球,假设前后椭球能量分数分别为 和 ,,得到前面椭球热源分布为
(3-10)
后半部分椭球热源分布函数将(3-10)中的 替换成 即可。
经过文献查找,对于不同的焊接情况,要适当的调整上述两个参数,美国T·S·Lsai在理论与实验结果的对比下,认为 取2/3, 取4/3,此时具有较好的模拟效果,本文取 ; [11]。
3.1.3. 组合热源
热源模型主要包含了集中热源模型、面热源模型、体热源模型,由于热源模型的选取会直接影响到数值模拟的结果,又由于以上三类热源模型片面的强调能量的点分布、面分布或者体积分布,针对不同的情况会产生较大的误差。如在焊接热源较远的研究区域内,采用经典理论Rosenthal-Rykalin公式时数值模拟较为准确,但这无法表现焊接热源的分布规律,这会产生较大的误差;而高斯面热源分布无法准确的描述焊缝熔池内部的形状;椭球体热源分布模拟时表面温度较低,所以都含有缺陷 [12]。
由于焊接的复杂以及单一热源的缺陷,逐渐产生了组合热源,组合热源的选取需要满足三个条件,即熔池的形状、热量能源分布结构和复合焊接,如激光焊接方法。本文由于采用激光焊接,以及铝板力学和物理性能,采用组合焊接方法:焊缝表面高斯热源,焊缝内部双椭球体热源的组合热源模型,这样不仅可以较精确的分析温度场,而且在应力场分析中,较精确的分析沿板厚方向的应力,具体分析如下。
组合热源中高斯热源控制表面熔池,椭球体热源控制深层液体,总的输入功率按照一定的比例分配,由等量关系可知,总输入功率等于表面输入功率与体积输入功率之和 [13]。
(3-11)
式中, 表示表面热源功率, 为体热源功率, 为总符号热源有效功率
(3-12)
(3-13)
式中, 为功率分配系数,其值为1/3
上述不仅考虑了激光焊接热源对焊件表面的影响,同时也考虑了液滴在熔池内的热源,这将更加精确的描述三维焊接中,温度场与应力场的变化。本文将对以上三种热源模型分别进行模拟。
3.2. 温度场有限元模型
本文采用整体为300 mm * 150 mm * 8 mm的铝板对接I型坡口进行焊接。焊缝处的单元尺寸控制在4 mm以内,初始温度设置为25℃。在建立几何模型时,可以利用三维对称结构,建立1/2模型。设温度初始值为Tinti;由于取了1/2对称结构,所以将焊件沿着y轴的一侧定义为对称边界;热源选择焊缝区域,在采用高斯热源时,为表面热源,在边界热源中选定焊缝区域上表面,设定热源加载公式Ein,即可生成高斯热源的加载模型;若采用双椭球热源,为体积热源,在窗口模型中选中整个焊缝区域,设定热源公式H1和H2,即可生成双椭球加载热源;若采用组合热源,则表面为高斯热源,焊缝内部为双椭球热源。由上述两种热源叠加而成,在几何模型上选中模型的整个上表面区域,点击对流热通量,定义传热系数为β,外部温度为Tinti;除以上设置的界面外,其余的界面均是绝热源。具体材料参数见表1。由于激光在板的焊缝区域沿着y方向移动,所以在移动热源的加载中,y是时间t的函数,具体为 ,然后代入到上述的热源公式中y的位置。由于激光焊接是不均匀的加热过程,所以在焊缝区域网格较密集,经过热影响区域到远离焊缝位置的单元逐渐稀疏,采用尺寸较大的单元。
Table 1. Material parameters
表1. 材料参数
4. 不同热源模型下的温度场分布
4.1. 高斯热源模型温度场分析
在P(焊接功率) = 1500 W,V(焊接速度) = 30 mm/s,R(入射光斑半径) = 2.5 mm的焊接工艺下,其余参数不变。热源在焊接过程中,随时间的变化,不同点温度不同。又由于随着激光的移动,温度先升高后降低,激光通过后的区域铝板会进入冷却阶段,所以在COMSOL设置中,设置激光在材料上运动时间为10 s,而后10 s进入冷却阶段。在同一位置节点,温度会随着时间的变化而变化,下面分别研究焊缝区域不同位置的温度变化,选取焊缝上的七个点分别为:y = −150 mm、y = −100 mm、y = −50 mm、y = 0 mm、y = 50 mm、y = 100 mm、y = 150 mm。温度随时间的变化曲线如图1所示,由图1可知焊缝区域温度先上升后降低,在焊缝不同位置有相同的变化规律;另外当热源经过焊接位置时,温度会急剧上升,但经过该点后温度缓慢下降,其原因在于该区域达到峰值后,由于温度差会向周围扩散,但并没有很快的完全扩撒,所以降低趋势比较缓慢,这与实际的焊接温度场分布情况相符合;同时可以发现冷却阶段的温度区域一致,且比初始温度高,这主要说明热通量并未完全扩散到整个铝板。
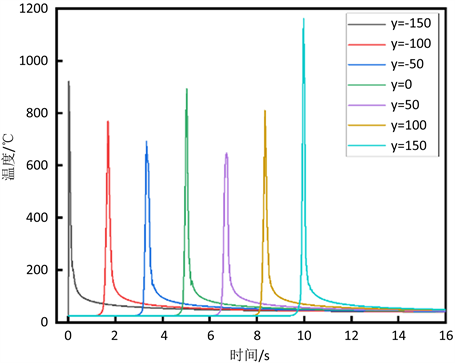
Figure 1. Temperature variation curve of weld zone
图1. 焊缝区域温度变化曲线图
4.2. 双椭球热源模型的温度场分析
双椭球热源属于体热源模型,是根据焊接熔池的形状做出的公式推到,主要参数包括熔宽(a)、熔深(b)、前椭半球长(Cf)、后椭半球长(Cr)。因此就不同的形状参数对焊接的温度场分布的影响进行分析;同时也分析了双椭球热源模型中椭圆扁平程度对温度场的影响。形状参数如表2所示。
Table 2. Shape parameters
表2. 形状参数
4.2.1. 形状参数对温度场的影响
首先保持其他定义参数不变,以a = 1.25 mm为基准,取同样间隔数值为步长,研究当熔宽(a)发生变化时,对温度场的影响,其中取焊缝区域特定点y = 0处为研究对象,其结果如图2(a)所示。随着a的增大,焊缝区域内的温度逐渐减小。从a = 1.25 mm时的1536℃降低a = 2.25 mm时的1331℃,温度相差205℃,但达到峰值的时间没有明显变化;冷却区域温度平缓,冷却时间基本一致,冷却值趋于一致,说明冷却阶段不受熔宽的影响。在保持其他定义参数不变,以b = 1.5 mm为基准,取同样间隔数值为步长,研究当熔深(b)发生变化时,对温度场的影响,具体如图2(b)所示。由图2(b)可以直观发现,随着熔深b的增大,某定点的峰值逐渐减小,从b = 1.5 mm时的1536℃降低至b = 3.5 mm时的1024℃,温度差为512℃,达到峰值的时间相差不大;但与图2(a)对比发现,当图2(b)中b的增加,使得材料加热与冷却的中间时间程相对于a增加时的中间时间程缩短,即曲线上升与下降时的坡度都比较倾斜,直观来看就是在短时间内材料加热与冷却的时间相对于a的影响是缩短的。在保持其他定义参数不变,以Cf = 2 mm为基准,取同样间隔数值为步长,研究当椭球前半轴长(Cf)发生变化时,对温度场的影响。如图2(c)所示。观察图2(c)发现,随着Cf的增大,整体的焊缝区域内的温度逐渐降低,由Cf = 2 mm时的1536℃降低至Cf = 4 mm时的1400℃,温度降低了136℃;同时随着Cf的增大,温度峰值的出现时间逐渐向右移动;冷却阶段温度逐渐趋于稳定,冷却时间趋于一致,冷却值趋于一致,说明椭球前半轴长不影响焊件的冷却阶段。在保持其他定义参数不变,以Cr = 2 mm为基准,取同样间隔数值为步长,研究当椭球前半轴长(Cr)发生变化时,对温度场的影响。如图2(d)所示。随着Cr的逐渐增大,在焊缝区域的温度峰值逐渐降低,从Cr = 7 mm处的1433.6℃降低至Cr = 11 mm处的1228.8℃,温度差为204.8℃;出现峰值整体时间偏左,冷却温度、冷却时间基本不受Cr的影响。
4.2.2. 椭球的扁平程度对温度场的影响
在研究双椭球热源模型时,引入椭圆扁平程度的度量,即离心率e。其概念为半焦距与半长轴的比值( ),其中半焦距为 。当 时,为圆;当 时,为椭圆;当 时,为抛物线;当 时,双曲线;其中 时,离心率越大,扁平程度越大,说明椭圆越扁,此时双椭球热源模型误差会变大,具体参数见表3。
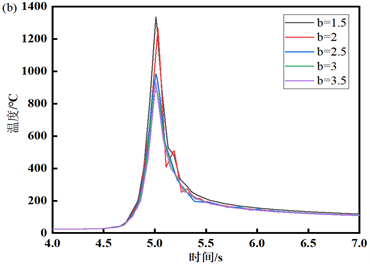
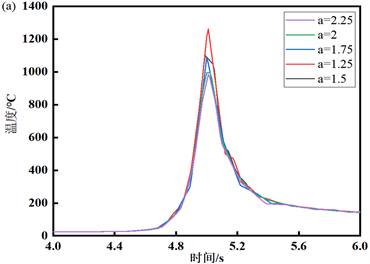
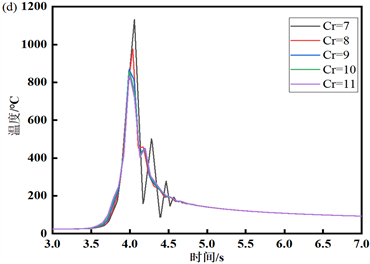

Figure 2. Chang curve of weld zone temperature with time: (a) different values of weld width a; (b) different values of melting depth b; (c) different values of the anterior ellipsometer Cf; (d) different values of the posterior ellipsometry Cr
图2. 焊缝区域温度随时间的变化曲线:(a) 熔宽a取值不同;(b) 熔深b取不同值;(c) 前椭半球长Cf取值不同;(d) 后椭半球长Cr取不同值
Table 3. Centrifuge selection
表3. 离心率选取
形状参数的选取是随机的,每个参数之间并没有必然联系,在计算离心率时,由于双椭球为不规则椭球形状,所以e的取值为每个椭半球的离心率的平均值。对三组不同参数模拟,得到图3所示的温度场云图。红色区域表示温度最高的位置,对比三组剖面温度场发现,随着e的逐渐增大,高温区域逐渐向外部扩展,且温度逐渐增大。
对焊缝区域的温度场模拟后处理,如图4所示。由图可知,在焊缝区域内,三组达到峰值的时间基本一致;A组峰值为972.8℃,B组峰值为1108℃,C组峰值为1125.6℃,其中B与C的温度差不大,而B、C与A的温度差大于100℃,即从总体上看,在 中,随着e的逐渐增大,在焊缝区域温度逐渐升高,即椭球越扁温度越高。
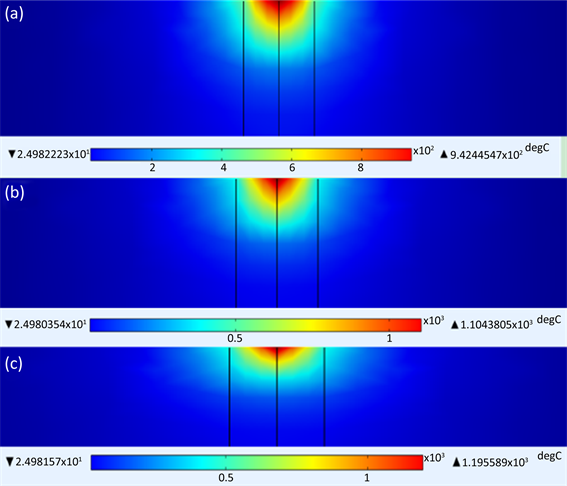
Figure 3. Temperature contour at different eccentricities: (a) temperature contour of group A; (b) temperature contour of group B; (c) temperature contour of group C
图3. 不同离心率下温度云图:(a) A组温度云图;(b) B组温度云图;(c) C组温度云图
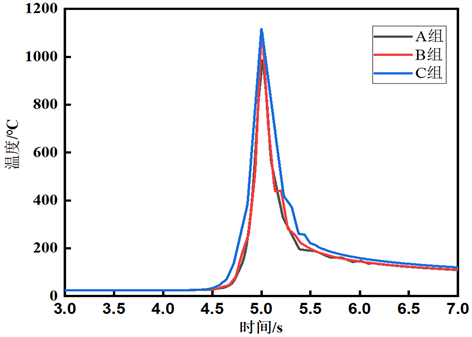
Figure 4. Change curve of weld area temperature
图4. 焊缝区域温度场变化曲线
4.3. 组合热源模型的温度场分析
基于组合热源,根据焊接的物理参数变化,研究在不同焊接参数(焊接速度(V)、入射光斑半径(Rin)、焊接功率(Pin))对焊件温度场的影响,参数设置见表4。本节采用高斯热源和双椭球热源模型的组合形式,由于高斯热源是面热源,在有限元模拟中,将其设置在焊缝区域的表面;而双椭球热源为体热源,所以将其设置在焊缝的整个区域内。将激光功率进行分配,功率分配系数 ,详见(3-12)和(3-13)。
Table 4. Welding parameters
表4. 焊接参数
本节讨论在(焊接速度(V)、入射光斑半径(Rin)、热输入功率(Pin)下,焊缝区域内温度场的变化。在焊缝区域,特定点的温度场随时间变化的曲线图如图5(a)。研究发现,当V = 0.01 m/s时,达到峰值的时间在15 s之后,此时的峰值为1408℃;当V=0.02m/s时,达到峰值的时间在8 s之后,峰值为1280℃;当V = 0.03 m/s时,出现峰值的时间接近6s,此时的峰值温度为1152℃;由此可知,随着焊接速度的增大,在焊缝区域内,温度逐渐降低。在焊缝区域,特定点的温度场随时间变化的曲线图如图5(b)所示。由图像可以发现,在焊缝区域,当Rin = 2 mm时,峰值温度为1488℃;当Rin = 3 mm时,峰值温度为1368℃;当Rin = 4 mm时,峰值温度为1280℃。所以随着入射光斑半径的增大,温度逐渐降低;在冷却区域,冷却时间基本一致,温度值趋于一致,即在冷却阶段光斑的大小不影响温度的变化。由图5(c)发现,Pin = 1500 W时,温度峰值为1280℃;Pin = 1800 W时,温度峰值为1635℃;Pin = 2000 W时,温度峰值为1805℃;即随着热输入功率的增大,在焊缝区域的温度也随之增大。
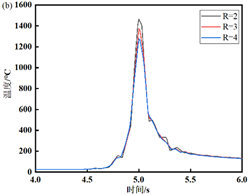
Figure 5. Change curve of weld zone temperature with time: (a) different values for V; (b) different values for Rin; (c) different values for Pin
图5. 焊缝区域温度随时间的变化曲线:(a) V取不同值;(b) Rin取不同值;(c) Pin取不同值
5. 结论
本文利用COMSOL软件,对I型坡口铝板进行三维数值模拟。分析了不同参数下,焊接过程中温度场的变化和分布规律,得出以下主要结论:
1、对比三种热源模型的温度场,在同等参数设置下,高斯热源的温度值最低,在800℃附近,随着热源模型的该进,温度值逐渐升高;在双椭球热源模型下,温度最大值上升为1000℃,温度上升了200℃;在组合热源模型中,温度为1600℃,温度相比双椭球热源上升了600℃,说明随着热源模型的改进,热源逐渐贴合实际热源时,焊件的温度场逐渐上升,数值模拟逐渐精确。
2、在双椭球热源模型中,研究了熔宽(a)、熔深(b)、椭球前半轴长Cf和椭球后半轴长Cr对温度场的影响。研究发现,随着形状参数的逐渐增大,温度场会逐渐减小;在冷却阶段,温度场的变化不受形状参数的影响。
3、在组合热源模型中,研究了焊接速度(V)、入射光斑半径(Rin)和热输入(Pin)对温度场的影响。结果发现,随着焊接速度的增大,焊缝区域温度场会逐渐降低,同时焊接速度不影响焊件的冷却阶段;随着入射光斑半径的增大,焊缝区域温度场逐渐降低,其变化不影响焊件的冷却阶段;随着热输入功率的逐渐增大,焊缝区域温度场逐渐增大,当热输入功率逐渐增大时,在冷却阶段的温度并不是趋于一致的,即在冷却阶段的同一时间下,会产生明显的温度差。
基金项目
国家自然科学基金(12002230);山西省应用基础研究计划面上青年基金项目(201901D211299);太原科技大学博士启动金(20192005);来晋优秀博士科研启动金(20202011)。
文章引用
申 强,李彦业. 铝板焊接过程中温度场的有限元模拟
Finite Element Simulation of Temperature Field during Aluminum Plate Welding[J]. 建模与仿真, 2022, 11(05): 1358-1368. https://doi.org/10.12677/MOS.2022.115128
参考文献
- 1. 薛家祥, 黄雯锦, 徐敏. 铝薄板高速DP-GMAW焊接性能的研究[J]. 焊接, 2016 (5): 471-473.
- 2. 冀伟, 张鹏, 姜红. 波形钢腹板梁T形接头焊接温度场分析[J]. 焊接, 2022(6): 8-14.
- 3. 庄其仁. 激光焊接温度场解析计算[J]. 华侨大学学报: 自然科学版, 2001, 22(3): 247-252.
- 4. 蔡志鹏, 赵海燕, 鹿安理, 等. 焊接数值模拟中分段移动热源模型的建立及应用[J]. 中国机械工程, 2002, 13(3): 208-210.
- 5. 蔡志鹏, 赵海燕, 吴甦, 等. 串热源模型及其在焊接数值模拟中的应用[J]. 机械工程学报, 2001, 37(4): 2 825-2843.
- 6. 王能庆, 童彦刚, 邓德安. 热源形状参数薄板焊接残余应力和变形的影响[J]. 焊接学报, 2012, 33(12): 97-100.
- 7. 程久欢, 陈俐, 于有生. 焊接热源模型的研究进展[J]. 焊接技术, 2004, 33(1): 13-15.
- 8. 姚相林, 周宏. 基于Ansys的Q235A焊接数值模拟[J]. 舰船科学技术, 2022, 44(13): 85-89.
- 9. 李陈峰, 金腾龙, 刘德怀, 张一凡, 刘涛. 铝合金加筋板焊接温度场和残余应力数值模拟[J]. 舰船科学技术, 2021, 43(23): 71-75.
- 10. 周文静, 杜柏松, 卢小明. 铝合金搅拌摩擦焊温度场数值模拟及参数影响分析[J]. 热加工工艺, 2021, 50(7): 156-160.
- 11. 谷京晨, 童莉葛, 黎磊, 等. 焊接数值模拟中热源的选用原则[J]. 材料导报, 2014, 28(1): 143-146.
- 12. 徐洲, 李晓延, 王小鹏, 等. 组合热源模型在焊接模拟中的应用现状与展望[J]. 材料导报, 2022, 36(6): 148-153.
- 13. 盖登宇, 褚元召, 李庆芬, 等. 组合热源模型在焊接数值模拟中的应用[J]. 焊接学报, 2009(5): 6461-6468.
