Statistics and Application
Vol.
08
No.
01
(
2019
), Article ID:
28903
,
6
pages
10.12677/SA.2019.81016
Predicting Tourist Number of Guangdong Province Based on Fractal Auto-Regressive Model
Huan Zhao, Weidong Fang
School of Mathematics, South China University of Technology, Guangzhou Guangdong

Received: Jan. 27th, 2019; accepted: Feb. 11th, 2019; published: Feb. 19th, 2019

ABSTRACT
An effective prediction on tourist number is good for government and related departments taking steps timely to cope with passenger flows. At the same time, it can provide proposal for development, planning and management of local economy. This article adopts monthly data of tourist number coming to Guangdong Province from 2001 to 2017, takes advantage of its long memory, establishes ARFIMA model, and separately predicts twelve months’ tourist numbers in 2017. The result shows that the prediction is effective by comparing true value with predicted value.
Keywords:Long Memory, ARFIMA Model, Fractional-Order Difference, Predict
基于分形自回归模型的广东省旅游人数预测
赵欢,方卫东
华南理工大学,数学学院,广东 广州

收稿日期:2019年1月27日;录用日期:2019年2月11日;发布日期:2019年2月19日

摘 要
对旅游人数进行有效预测,有利于政府及相关部门及时采取应对客流量的措施,同时也为当地旅游业及经济发展、规划、管理提供参考意见。本文采用2001~2016年广东省接待游客人数的月度数据,利用其具有的长记忆性,建立ARFIMA (分型差分自回归)模型,并对2017年12个月的来广旅游人数分别进行预测,比较真实值与预测值,结果表明预测效果较好。
关键词 :长记忆性,ARFIMA模型,分数阶差分,预测

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着我国经济的快速发展,国民生活水平日益提高,外出旅游越来越成为人们休闲娱乐的方式之一,旅游业带来经济快速增长的同时,景区中大量游客的涌入也给当地交通、环境等造成压力,因此,准确预测旅游人数,以便当地政府以及相关部门及时采取应对措施显得至关重要。关于旅游人数的方法预测已经有很多人做了相关的研究, Granger、Joyeux (1980) [1],Hosking (1981)分别独立提出ARFIMA模型,在此基础上Granger [2] 进行了深入研究。冯春山等(2005) [3],对石油价格数据建立ARFIMA模型,结果表明考虑了长记忆性的ARFIMA模型效果好于短记忆性ARMA (自回归移动平均)模型。姚瑾(2006) [4] 等,利用ARFIMA模型对香港恒生指数进行预测,结果模型预测结果是失效的,这是因为模型本身特点以及非线性系统对初始条件敏感性造成的,翁钢民,郑竹叶,刘洋(2009) [5],利用ARFIMA模型对我国入境旅游人数进行了预测,结果表明ARFIMA比ARIMA (自回归求和滑动平均)和SARIMA (季节性差分自回归滑动)预测效果好。王振寰,孙鹏哲(2014) [6] 等,利用ARFIMA模型对内蒙古农林牧渔业总产值进行研究,结果表明拟合较为准确,误差在可控范围内。刘凯等(2017) [7],利用分数阶差分对煤炭消费量进行预测,结果表明ARFIMA模型预测偏差更小,更接近实际值。陈鹏(2018) [8] 等,对黄金价格建立ARFIMA-GARCH模型族,很好地反映了黄金价格波动规律。本文采用ARFIMA模型,对旅游人数序列实行分数阶差分,能够避免过度差分造成的时间序列数据中信息的损失,保存原时间序列数据中的有用特征,减小建模和参数估计中的偏差。
2. ARFIMA模型及预测
2.1. ARFIMA模型定义
如果 是平稳时间序列,满足分数阶差分方程 ,则称 服从ARFIMA(p,d,q)。其中B为滞后算子, 是白噪声序列, 是分数差分算子, , 与 分别是p、q阶的平稳滞后多项式算子,且在复平面内根的模大于1, , 。
2.2. ARFIMA模型建立
ARFIMA模型建立具体步骤如下:
1) 判断序列平稳性:根据序列的时序图及自相关图特征初步判断序列的平稳性,进一步可通过ADF检验进行辅助判断。
2) 数据预处理及纯随机性检验:对表现非平稳的序列清理其中的波动趋势,使之平稳;对表现平稳的序列对其进行纯随机性检验。
3) 判断序列的长记忆性及清除短记忆因素:对得到的平稳非白噪声序列,画出自相关图,若函数图象呈多项式速度缓慢递减,在滞后阶数很大时仍有较强的自相关性,表明序列具有长记忆性。通过建立自回归AR(P)模型,清除短影响因素。
4) 分数阶差分:通过R/S分析法计算长记忆性的平稳非白噪声序列的Hurst指数,利用 求出分数阶差分的数值,对序列进行分数阶差分。
5) ARFIMA模型定阶:对分数阶差分后的序列建立ARMA(p,q)模型,确定p,q的值,即得ARFIMA(p,d,q)。
6) 估计模型中未知参数 的值。
7) 检验模型有效性并进行预测。
2.3. ARFIMA模型预测
下面利用2001~2016年广东省接待游客过夜人数(万人次)的月度数据 [9] 建立ARFIMA模型(从2001年1月至2016年12月共192个数据),并利用模型进行向后12步预测,对2017年一共12个月旅游人数分别进行预测。建模过程如下:
1) 画出序列 的时序图以及自相关图,图1是时序图。
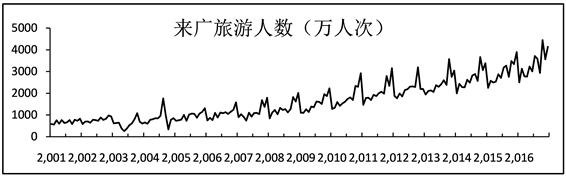
Figure 1. Traveling number sequence diagram
图1. 旅游人数时序图
由图2自相关图可知,来广旅游人数随时间的变化而变化,总体表现为上升的趋势。
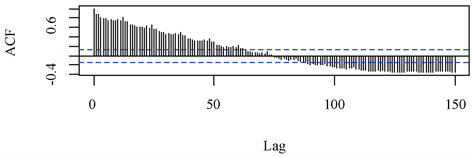
Figure 2. Traveling number autocorrelogram
图2. 旅游人数自相关图
从自相关图中可以看出序列自相关系数缓慢递减到0,在滞后阶数较大的范围内,自相关系数先正后负,且表现出三角对称性,由此可大致判断序列是具有单调趋势且非平稳的。一般地,考虑对序列进行一阶差分,画出差分后的自相关图发现:当间隔是周期12的倍数时相关性较强。继续对序列进行一次季节差分,得到差分后 的时序图 ,如图3所示。

Figure 3. The sequence diagram after the first difference and the first seasonal difference
图3. 一阶差分、一次季节差分后的时序图
此时序列基本围绕一个固定数值波动,初步判断是稳定的,为确保准确,利用ADF检验,结果如图4所示。

Figure 4. ADF test
图4. ADF检验
P值是小于0.05,因此可以判定序列平稳。
2) 对 进行纯随机性检验,计算得出在不同滞后阶数下,Q检验统计量的P值均远小于0.05,因而是平稳非白噪声序列,且蕴含的值得提取的信息。
3) 对 建立自回归AR(P)模型,清除短影响因素,根据AIC最小信息量准则选定P = 12,模型参数分别为−0.6185,−0.6730,−0.4458,−0.4331,−0.2784,−0.3071,−0.1013,−0.1086,−0.0394,0.1071,0.1742,−0.1343,利用AR(12)估计的值建立置信水平为95%的置信区间,删除掉 中35个奇异值,得到新的序列 ,过程如图5所示。

Figure 5. Clear short memory factor sequence diagram
图5. 清除短记忆因素时序图
4) 计算分数阶差分d:运用修正的R/S分析法计算得到Hurst [10] 指数为0.5788384,根据公式
,即得 ,将分数差分后的序列记为 ,则有 ,且满足 ,是均值为0的ARMA(p,q)序列。
对 建立ARMA模型,根据自相关和偏自相关图的滞后阶数大致确定p,q范围,再利用AIC准则,选择使其值最小对应的模型为ARFIMA(1,0.0788384,0),不同模型AIC值如表1所示。
Table 1. Model choose
表1. 模型选择
5) 利用R软件可得模型的参数方程为 ,
则ARFIMA的参数方程为
,其中 。
6) 对模型的残差进行显著性检验,得到在各阶延迟下的统计量LB统计量t的P值都远大于0.05,对系数进行显著性检验,结果表明系数显著非0,即模型拟合有效,利用模型ARFIMA(1,0.0788384,0)对2017年来广的旅游人数进行预测,并与真实值进行比较,如表2所示。
Table 2. True value and predicted value
表2. 实际值与预测值
由图中可以看出预测的结果总体较为理想,除9月份的相对误差较大以外,其余月份的相对误差均在较为合理的范围内。图6是真实值与预测值的比较图,以便我们更加方便、直观了解模型拟合效果。
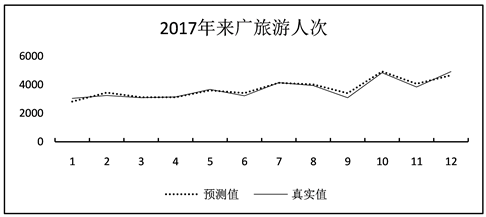
Figure 6. Autocorrelation function of agriculture and forestry’s index
图6. 实际值与预测值拟合
3. 结语
随着国民生活水平的日益提高,以及思想观念的转变,外出旅游已经越来越成为人们娱乐放松的选择之一,基于旅游人数具有长记忆性规律,本文以2001年到2016年的来广旅游人数月度数据为依据,建立ARFIMA(1,0.0788384,0)模型,并进行了12步预测,得到2017年全年12个月的来广月度数据,与真实值比较发现预测结果较好,为今后旅游业人数预测提供有效依据,方便政府及部门对旅游业发展做出合理规划及应对措施。
文章引用
赵 欢,方卫东. 基于分形自回归模型的广东省旅游人数预测
Predicting Tourist Number of Guangdong Province Based on Fractal Auto-Regressive Model[J]. 统计学与应用, 2019, 08(01): 143-148. https://doi.org/10.12677/SA.2019.81016
参考文献
- 1. Granger, C.W.J. and Joyeux, R. (1980) An Introduction to Long-memory Time Series Models and Fractional Differ-encing. Journal of Time Series Analysis, 1, 15-29. https://doi.org/10.1111/j.1467-9892.1980.tb00297.x
- 2. Granger, C.W.J. (1980) Long Memory Relationships and the Aggregation of Dynamic Models. Journal of Econometrics, 14, 227-238. https://doi.org/10.1016/0304-4076(80)90092-5
- 3. 冯春山, 吴家春, 蒋馥. 石油价格的ARFIMA模型预测研究[J]. 上海理工大学学报, 2005, 27(6): 539-542.
- 4. 姚瑾. 应用ARFIMA模型对金融时间序列长期记忆性的研究[D]: [硕士学位论文]. 沈阳: 东北大学, 2006.
- 5. 翁钢民, 郑竹叶, 刘洋. 我国入境旅游预测: 基于ARFIMA模型的研究[J]. 商业研究, 2009(6): 1-4.
- 6. 王振寰, 孙鹏哲, 陶伟庆, 邓茗予, 杨婷. 基于ARFIMA模型的内蒙古农林牧渔业总产值研究[J]. 内蒙古师范大学学报(自然科学汉文版), 2014(6): 696-698.
- 7. 刘凯, 张晞. 基于分数阶差分ARIMA模型的煤炭消费预测[J]. 矿业科学学报, 2017(5): 85-92.
- 8. 陈鹏, 李星野. 基于ARFIMA-GARCH模型族的黄金价格预测分析[J]. 电子商务, 2018(5): 42-44.
- 9. 广东省统计信息网[EB/OL]. http://www.gdstats.gov.cn/tjsj/lyy/.
- 10. Pai, J.S. and Ravishanker, N. (1996) Bayesian Modelling of ARFIMA Processes by Markov Chain Monte Carlo Methods. Journal of Forecasting, 15, 63-82. https://doi.org/10.1002/(SICI)1099-131X(199603)15:2<63::AID-FOR606>3.0.CO;2-5
