Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18443,7
pages
10.12677/AAM.2016.53055
The Modified Simple Equation Method and the Exact Solutions for the sine-Gordon Equation and the Generalized Variable-Coefficient KdV-mKdV Equation
Lingfeng Xiao, Sirendaoerji
College of Mathematics Science, Inner Mongolia Normal University, Hohhot Inner Mongolia

Received: Aug. 16th, 2016; accepted: Aug. 27th, 2016; published: Aug. 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The modified simple equation method is used to construct the exact solutions for the sine-Gordon equation and the generalized variable-coefficient KdV-mKdV equation. Some exact solutions of the hyperbolic function form for the sine-Gordon equation and the generalized variable-coefficient KdV-mKdV equation are derived by the method. When taking special values of the parameters, the exact traveling wave solutions of the equations are derived from the exact solutions.
Keywords:The Modified Simple Equation Method, sine-Gordon Equation, Variable-Coefficient KdV-mKdV Equation, Exact Solutions

修正的简单方程法与sine-Godon方程和广义的变系数KdV-mKdV方程的精确解
肖玲风,斯仁道尔吉
内蒙古师范大学数学科学学院,内蒙古 呼和浩特

收稿日期:2016年8月16日;录用日期:2016年8月27日;发布日期:2016年8月30日

摘 要
本文用修正的简单方程法对sine-Gordon方程和广义的变系数KdV-mKdV方程进行求解,并给出了它们的行波解,当给参数取特殊值时,便可以得到相应的精确行波解。
关键词 :修正的简单方程法,sine-Gordon方程,变系数KdV-mKdV方程,精确解

1. 引言
求解非线性发展方程是非线性理论的一个重要课题,迄今为止,学者们已经利用Painlevé分析法 [1] [2] 、Bäcklund变换法 [3] 、辅助方程法 [4] 、G'/G—展开法 [5] 等对非线性发展方程进行了求解。受G'\G—展开法的启发,近来学者们又提出“修正的简单方程法 [6] [7] ”并对Fitzhugh-Nagumo方程和Sharma-Tasso- Olver方程等许多常系数非线性发展方程进行精确求解。但目前为止未见用此方法来求解该方法无法直接运用的方程,如sine-Gordon方程 [8] [9] 以及变系数非线性发展方程。故本文旨在利用该方法给出sine- Gordon方程和广义的变系数KdV-mKdV方程 [10] 的精确行波解。
sine-Gordon方程在非线性光学、等离子物理、固体物理等自然科学领域中有着广泛的应用;在流体力学和等离子体中,广义变系数非等谱KdV-mKdV方程用来刻画弱非线性长波在KdV介质中传播,因此这两个方程都是有重要物理背景的模型方程。因此寻找sine-Gordon方程和广义的变系数KdV-mKdV方程的精确解在理论和实际应用中有着至关重要的意义。
2. sine-Gordon方程
下面考虑用修正的简单方程法求解sine–Gordon方程
 (2.1)
(2.1)
的问题。为此作变换
 ,则
,则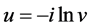 (2.2)
(2.2)
则可将方程(2.1)转化为
 (2.3)
(2.3)
再作行波变换
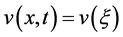 ,
,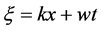 (2.4)
(2.4)
并将(2.4)代入(2.3)得到
 (2.5)
(2.5)
利用齐次平衡原则,平衡(2.5)中的最高阶导数项v³和非线性项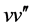 和
和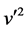 ,知n = 2,故可设
,知n = 2,故可设
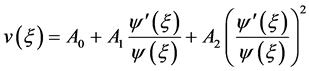 ,
,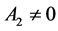 (2.6)
(2.6)
把(2.6)代入(2.5)后比较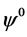 ,
, ,
,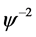 ,
,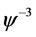 ,
,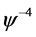 ,
,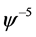 ,
,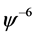 的系数可得
的系数可得
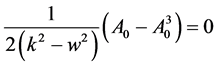 (2.7)
(2.7)
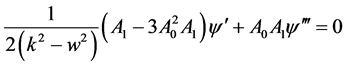 (2.8)
(2.8)
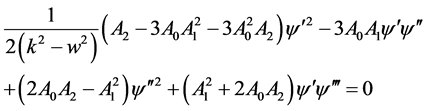 (2.9)
(2.9)
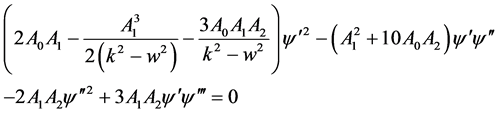 (2.10)
(2.10)
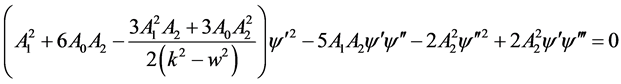 (2.11)
(2.11)
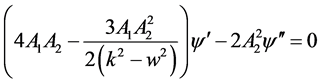 (2.12)
(2.12)
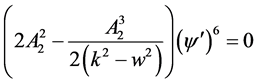 (2.13)
(2.13)
由(2.7)可得: ;由(2.13)可得:
;由(2.13)可得: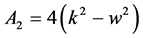
1) 当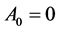 时,(2.5)无(2.6)形式的解
时,(2.5)无(2.6)形式的解
2) 当 时,(2.8)~(2.12)化为常微分方程组
时,(2.8)~(2.12)化为常微分方程组
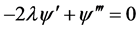 (2.14)
(2.14)
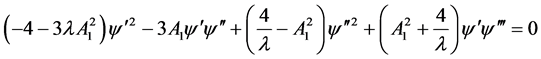 (2.15)
(2.15)
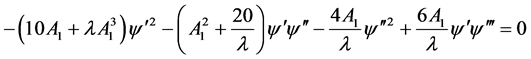 (2.16)
(2.16)
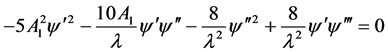 (2.17)
(2.17)
 (2.18)
(2.18)
其中: ,
,
由(2.18)可得
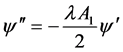 ,则
,则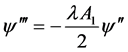 (2.19)
(2.19)
把(2.19)代入(2.14)可得
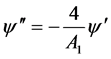 ,则
,则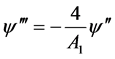 (2.20)
(2.20)
把(2.20)代入(2.15)可得
 ,则
,则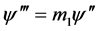 ,
, (2.21)
(2.21)
把(2.21)代入(2.16)可得
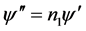 ,则
,则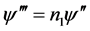 (2.22)
(2.22)
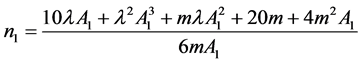 (2.23)
(2.23)
把(2.22)代入(2.17)可得
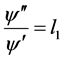 ,
, (2.24)
(2.24)
对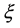 积分两次有
积分两次有
 (2.25)
(2.25)
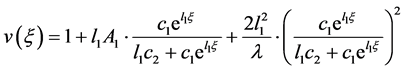 (2.26)
(2.26)
因此
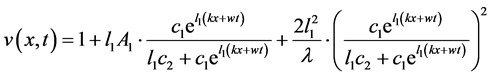 (2.27)
(2.27)
从而
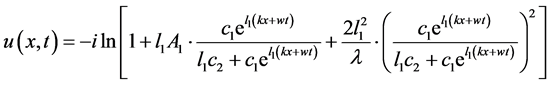 (2.28)
(2.28)
取 ,
,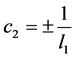 ,得到sine-Gordon方程的精确孤波解
,得到sine-Gordon方程的精确孤波解
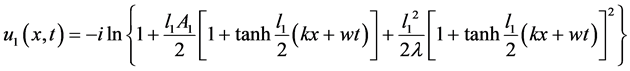 (2.29)
(2.29)
 (2.30)
(2.30)
3) 当 时,(2.8)~(2.12)化为常微分方程组
时,(2.8)~(2.12)化为常微分方程组
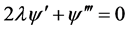 (2.31)
(2.31)
 (2.32)
(2.32)
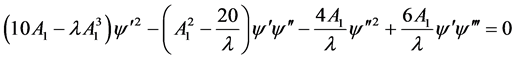 (2.33)
(2.33)
 (2.34)
(2.34)
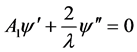 (2.35)
(2.35)
完全类似于方程组(2.14)~(2.18)的求解过程,我们得到
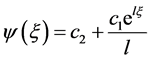 ,
, (2.36)
(2.36)
 ,
,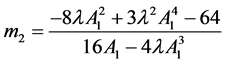 (2.37)
(2.37)
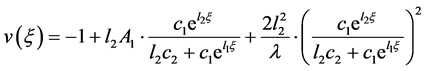 (2.38)
(2.38)
因此
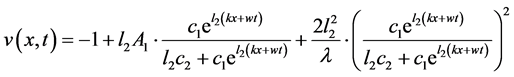 (2.39)
(2.39)
从而
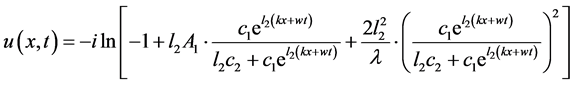 (2.40)
(2.40)
取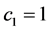 ,
,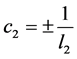 ,得到sine-Gordon方程的精确孤波解
,得到sine-Gordon方程的精确孤波解
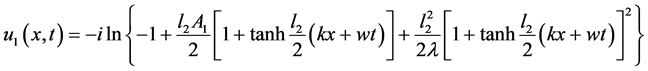 (2.41)
(2.41)
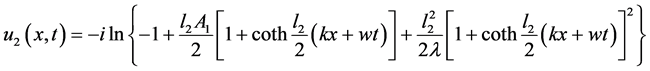 (2.42)
(2.42)
3. 广义变系数KdV-mKdV方程
广义变系数KdV-mKdV方程的形式为
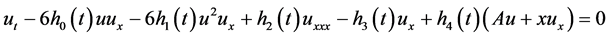 (3.1)
(3.1)
利用齐次平衡原则,平衡(3.1)中的最高阶导数项和最高幂次的非线性项,得 。于是,(3.1)有如下形式的形式解
。于是,(3.1)有如下形式的形式解
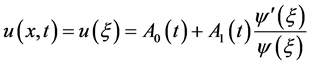 ,
, ,
,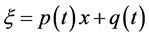 (3.2)
(3.2)
把(3.2)代入(3.1),比较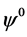 ,
,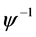 ,
,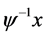 ,
,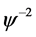 ,
, ,
,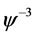 ,
,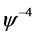 的系数得
的系数得
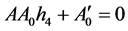 (3.3)
(3.3)
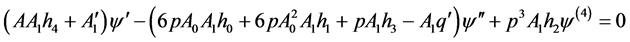 (3.4)
(3.4)
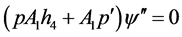 (3.5)
(3.5)
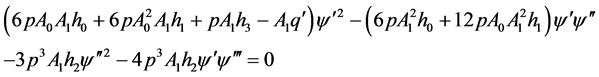 (3.6)
(3.6)
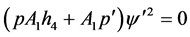 (3.7)
(3.7)
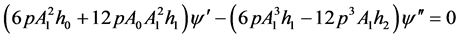 (3.8)
(3.8)
 (3.9)
(3.9)
由(3.3)可得: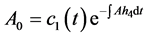 ,由(3.5)和(3.7)可得:
,由(3.5)和(3.7)可得: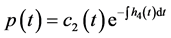
由(3.9)可得: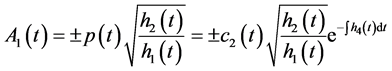
由(3.8)可得:
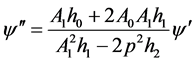 (3.10)
(3.10)
把(3.10)代入(3.6)得到:
 (3.11)
(3.11)
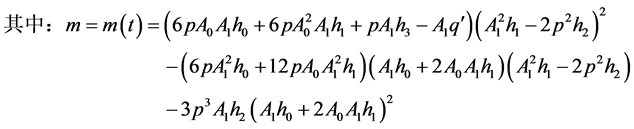

把(3.11)代入(3.4)可得:
 (3.12)
(3.12)
其中: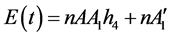 ,
,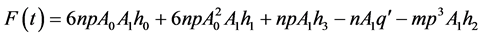
给(3.12)的两端对 积分两次可得:
积分两次可得:
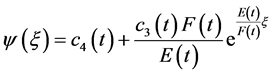 (3.13)
(3.13)
从而:
 (3.14)
(3.14)
于是
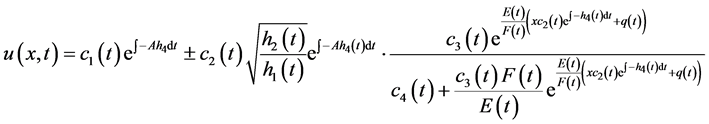 (3.15)
(3.15)
若令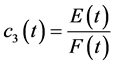 ,
,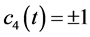 ,得到广义变系数KdV-mKdV方程的精确行波解如下
,得到广义变系数KdV-mKdV方程的精确行波解如下
 (3.16)
(3.16)
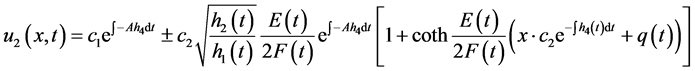 (3.17)
(3.17)
本文把修正的简单方程法推广到求解sine-Gordon方程和变系数方程中,得到sine-Gordon方程和广义变系数KdV-mKdV方程的精确孤波解。鉴于修正的简单方程法是受G'/G展开法的启发产生的一种新方法,因此,如果能够类似于G'/G-展开法的推广将此方法进行推广就有可能给出非线性发展方程的其他类型的精确解。
基金项目
国家自然科学基金资助项目(11261037, 10461006);内蒙古自然科学基金资助项目(2014MS0111);内蒙古师范大学“十百千”人才培养工程资助项目(RCPY-2-2012-K-033);内蒙古师范大学研究生科研创新基金资助项目(CXJJS15073);内蒙古自治区研究生教育创新计划资助项目。
文章引用
肖玲风,斯仁道尔吉. 修正的简单方程法与sine-Godon方程和广义的变系数KdV-mKdV方程的精确解
The Modified Simple Equation Method and the Exact Solutions for the sine-Gordon Equation and the Generalized Variable-Coefficient KdV-mKdV Equation[J]. 应用数学进展, 2016, 05(03): 443-449. http://dx.doi.org/10.12677/AAM.2016.53055
参考文献 (References)
- 1. Alowitz, M.J., Ramani, A. and Segur, H. (1978) Nonlinear Evolution Equations and Ordinary Differential Equations of Painlevé Type. Lettere al Nuovo Cimento, 23, 333-338. http://dx.doi.org/10.1007/BF02824479
- 2. Weiss, J., Tabor, M. and Carnevale, G. (1983) The Painlevé Property for Partial Differential Equations. Journal of Mathematical Physics, 24, 522. http://dx.doi.org/10.1063/1.525721
- 3. Wang, Y.-H. and Chen, Y. (2012) Bäcklund Transformations and Solutions of a Gene-ralized Kadomtsev-Petviashvili Equation. Communications in Theoretical Physics, 57, 217-322. http://dx.doi.org/10.1088/0253-6102/57/2/10
- 4. Sirendaoerji, T. (2006) New Exact Solitary Wave for Nonlinear Wave Equation with Fifth-Order Strong Nonlinear Term Constructed by Hyperbolic Function Type of Auxiliary Equation. Acta Physica Sinica, 55, 13-18.
- 5. Wang, M.L., Li, X.Z. and Zhang, J.L. (2008) The G'/G-Expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423. http://dx.doi.org/10.1016/j.physleta.2007.07.051
- 6. Khan, K. and Akbar, M.A. (2013) Exact and Solitary Wave Solutions for the Tzitzeica-Dodd-Bullough and the Modified KdV-Zakharov-Kuznetsov Equations Using the Modified Simple Equation Method. Ain Shams Engineering Journal, 4, 903-909. http://dx.doi.org/10.1016/j.asej.2013.01.010
- 7. 张哲, 李德生. 修正的BBM方程新的精确解[J]. 原子与分子物理学报, 2013, 30(5).
- 8. Rubinstein, J. (1970) sine-Gordon Equation. Journal of Mathematical Physics, 11, 258-266. http://dx.doi.org/10.1063/1.1665057
- 9. Bratsos, A.G. (2007) The Solution of the Two-Dimensional sine-Gordon Equation Using the Method of Lines. Journal of Computational and Applied Mathematics, 206, 251-277.
- 10. Meng, G.-Q., Gao, Y.-T., Yu, X., Shen, Y.-J. and Qin, Y. (2012) Painlevé Analysis, Lax Pair, Bäcklund Transformation and Multi-Soliton Solutions for a Generalized Variable-Coefficient KdV-mKdV Equation in Fluids and Plasmas. Physica Scripta, 85, 055010. http://dx.doi.org/10.1088/0031-8949/85/05/055010