Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19068,10
pages
10.12677/AAM.2016.54081
Boundary Value Problems for Second Order Difference Equations Containing Both Advance and Retardation
Jialin Xu, Zhan Zhou
School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong

Received: Nov. 4th, 2016; accepted: Nov. 20th, 2016; published: Nov. 28th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, the boundary value problems for a class of second order nonlinear difference equations containing both advance and retardation are studied. First, a variational functional corresponding to the boundary value problems as aforementioned is established. Next, the existence of solutions of the boundary value problems is transformed into the existence of critical points for the corresponding functional. Then, by using Mountain Pass Lemma, the existence of critical points of the functional is obtained, and thus the existence of solutions for the initial boundary value problems is also obtained.
Keywords:Second Order Difference Equations, Boundary Value Problems, Mountain Pass Lemma

具有超前和滞后的二阶差分方程的边值问题
徐佳琳,周展
广州大学数学与信息科学学院,广东 广州

收稿日期:2016年11月4日;录用日期:2016年11月20日;发布日期:2016年11月28日

摘 要
本文研究了一类具有超前和滞后的二阶非线性差分方程的边值问题。首先建立边值问题对应的变分泛函,然后将边值问题的解的存在性转化为相应泛函的临界点的存在性,再利用山路引理得到该泛函临界点的存在性,进而得到所求边值问题解的存在性。
关键词 :二阶差分方程,边值问题,山路引理

1. 引言
记 ,
, 及
及 分别表示自然数集,整数集和实数集。任取
分别表示自然数集,整数集和实数集。任取 满足
满足 ,记
,记 。
。 表示向量的转置。
表示向量的转置。
考虑具有超前和滞后的二阶非线性差分方程
 (1.1)
(1.1)
在混合边值条件
 (1.2)
(1.2)
下解的存在性。其中 为向前的差分算子,定义为
为向前的差分算子,定义为 。
。 是一个实序列,
是一个实序列, 满足
满足 A和B是常数。
A和B是常数。
方程(1.1)可看作如下具有超前和滞后的泛函微分方程的离散类似。
 (1.3)
(1.3)
在参考文献 [1] 中,Smets和Willem得到了类似方程(1.3)格动力系统孤立波解的存在性,而且方程(1.3)包含下列方程
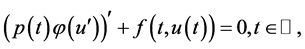 (1.4)
(1.4)
该方程在核物理、气体动力学、渗透介质理论和等离子体物理等领域中有广泛的应用前景,许多作者研究过这类方程,参见 [2] 。
2003年开始,临界点理论被用来研究了二阶超线性差分方程的周期解和次调和解的存在性,后来临界点理论也被应用于研究差分方程的边值问题,许多学者对方程(1.1)的一些特殊情形进行了深刻的讨论,得出了一系列有意义的结果,参见 [3] - [8] 。然而据我们所知,到目前为止,用临界点方法讨论方程(1.1)边值问题的文献很少(见 [9] [10] [11] [12] [13] ),因为方程(1.1)中 依赖于
依赖于 及
及 ,而在文 [3] - [8] 中建立泛函的方法面对我们的情况则无能为力。
,而在文 [3] - [8] 中建立泛函的方法面对我们的情况则无能为力。
下面我们介绍近几年通过临界点理论来研究方程(1.1)的特殊情形的解的存在性的相关结论。
2009年开始,石海平利用临界点理论给出了下列二阶非线性泛函差分方程
 (1.5)
(1.5)
在边值条件(1) 或(2)
或(2)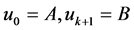 或(3)
或(3)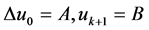 或(4)
或(4) 下解的存在性和多重性的充分条件,其中
下解的存在性和多重性的充分条件,其中 是Jacobi算子,参见 [11] 。
是Jacobi算子,参见 [11] 。
在参考文献 [14] 中,作者讨论了以下二阶差分方程
 (1.6)
(1.6)
在边值条件
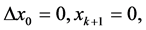 (1.7)
(1.7)
下解的存在性。
在参考文献 [12] 中,作者讨论了以下二阶差分方程
 (1.8)
(1.8)
在边值条件
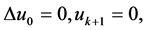 (1.9)
(1.9)
下解的存在性,其中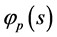 是Laplacian算子。
是Laplacian算子。
在参考文献 [13] 中,作者讨论了以下二阶差分方程
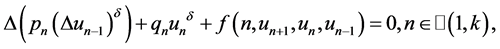 (1.10)
(1.10)
周期解与次调和解的存在性,其中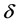 表示正奇数的比。
表示正奇数的比。
然而,我们了解到很多文献都是研究方程(1.1)特殊情形的二阶或高阶差分方程周期解的存在性,对差分方程边值问题的研究相对来说较少。出于以上考虑,本文的目的就是利用临界点方法研究二阶非线性差分方程边值问题(1.1)~(1.2)解的存在性,所采用的方法主要是利用山路引理结合变分技巧。
2. 变分框架及基本引理
为了运用临界点理论,我们将建立(1.1)~(1.2)的变分框架并给出一些必要的引理。
定义 上的内积如下:
上的内积如下:
 (2.1)
(2.1)
由 上的内积可以诱导空间
上的内积可以诱导空间 上的范数:
上的范数:
 (2.2)
(2.2)
对任意的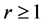 ,我们可以定义
,我们可以定义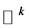 上的另一种范数:
上的另一种范数:
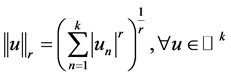 (2.3)
(2.3)
则存在常数 ,使得
,使得 ,且
,且
 (2.4)
(2.4)
其中 。
。
下面我们建立边值问题(1.1)~(1.2)的变分框架。设存在泛函 且
且 ,满足
,满足

考虑定义在 的泛函
的泛函
 (2.5)
(2.5)
 ,其中
,其中 。
。
根据边值条件(1.2),我们能计算 的Fréchet导数为:
的Fréchet导数为:

因此, 是
是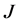 在
在 的临界点,即
的临界点,即 当且仅当满足
当且仅当满足 的
的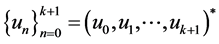
是边值问题(1.1)~(1.2)的解。因此,边值问题(1.1)~(1.2)解的存在性等价于定义在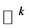 上泛函
上泛函 的临界点的存在性。
的临界点的存在性。
设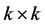 矩阵
矩阵 为
为

直接验证可知, 是正定矩阵,记它的特征值为
是正定矩阵,记它的特征值为 。不妨设
。不妨设
 (2.6)
(2.6)
定义2.1设 是实的Banach空间,
是实的Banach空间, ,即
,即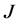 是定义在
是定义在 上的连续Fréchet可微的泛函,称泛函
上的连续Fréchet可微的泛函,称泛函 满足Palais-Smale条件(简称P.S.条件),如果对任意的序列
满足Palais-Smale条件(简称P.S.条件),如果对任意的序列 ,若
,若 有界且
有界且 ,则
,则 在
在 中存在收敛子列。
中存在收敛子列。
记 为在
为在 上中心在原点半径为
上中心在原点半径为 的开球,
的开球, 为
为 的边界。
的边界。
引理2.1 (山路引理) [15] 设 是实Banach空间,
是实Banach空间,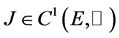 且在
且在 上满足P.S.条件,
上满足P.S.条件,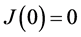 ,且有
,且有
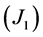 存在常数
存在常数 ,使得
,使得 ;
;
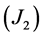 存在
存在 使得
使得 ,
,
则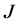 存在一个临界值
存在一个临界值 ,且
,且
 (2.7)
(2.7)
其中
 (2.8)
(2.8)
3. 主要结论及其证明
设

先给出一些条件:
 存在常数
存在常数 和
和 使得
使得

 存在常数
存在常数 和
和 使得
使得
 (3.1)
(3.1)
 存在常数
存在常数 和
和 ,使得
,使得

 存在常数
存在常数 和
和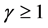 使得
使得
 (3.2)
(3.2)
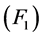 对任意的
对任意的 ,存在泛函
,存在泛函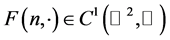 且
且 ,满足
,满足

 存在泛函
存在泛函 ,且存在常数
,且存在常数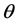 满足
满足 ,使得
,使得
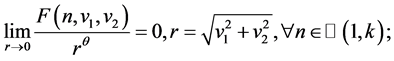
 对任意的
对任意的 ,存在常数
,存在常数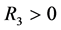 以及
以及 ,使得
,使得
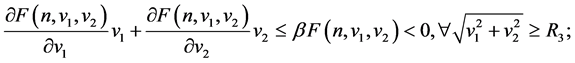 (3.3)
(3.3)
 对任意的
对任意的 ,有
,有 ;
;
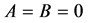
 。
。
注3.1 (3.1)蕴涵存在常数 使得
使得
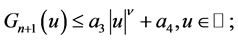
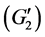
注3.2 (3.2)蕴涵存在常数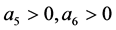 使得
使得
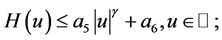
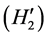
注3.3 (3.3)蕴涵存在常数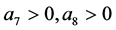 使得
使得
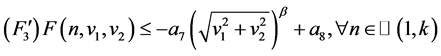 。
。
主要结论及其证明如下:
定理3.1若条件 ,
,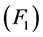 及
及 成立,且
成立,且
 对任意的
对任意的 ,存在常数
,存在常数 ,使得
,使得
 (3.4)
(3.4)
则边值问题(1.1)~(1.2)至少存在一个解。
注3.4 (3.4)蕴涵存在常数 ,使得
,使得
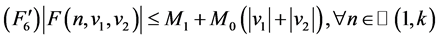 。
。
证 对任意的 ,
,

由 的连续性,上式表明泛函
的连续性,上式表明泛函 有下界,故
有下界,故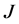 在某点
在某点 达到最小值。显然,
达到最小值。显然, 是泛函
是泛函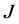 的临界点。证毕。
的临界点。证毕。
注3.5 当 时,其中
时,其中 表示正奇数的比,
表示正奇数的比, 是实序列,若条件
是实序列,若条件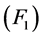 ,
, ,
,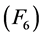 成立,且
成立,且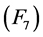 对任意的
对任意的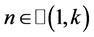 ,有
,有 ,则边值问题(1.1)~(1.2)至少存在一个解。
,则边值问题(1.1)~(1.2)至少存在一个解。
定理3. 若条件 ,
, ,
, 及
及 成立,且
成立,且 对任意的
对任意的 ,有
,有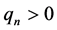 ,则边值问题(1.1)~(1.2)至少存在一个解。
,则边值问题(1.1)~(1.2)至少存在一个解。
证 对任意的 ,由
,由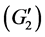 ,
, 有
有

由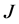 的连续性,上式表明泛函
的连续性,上式表明泛函 有上界,故
有上界,故 在某点
在某点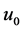 达到最大值。显然,
达到最大值。显然, 是泛函
是泛函 的临界点。证毕。
的临界点。证毕。
定理3.3 若条件 ,
, ,
, 及
及 ~
~ 成立,则边值问题(1.1)~(1.2)至少存在两个解。
成立,则边值问题(1.1)~(1.2)至少存在两个解。
为了方便定理3.3的证明,我们先证明两个引理:
引理3.1 若条件 ,
, ,
,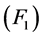 及
及 ~
~ 成立,则
成立,则 在
在 上有上界。
上有上界。
证 对任意的 ,有
,有
 (3.5)
(3.5)
由 知,存在
知,存在 ,使得对任意的
,使得对任意的 。证毕。
。证毕。
引理3.2 若条件 ,
, ,
, 及
及 ~
~ 成立,则
成立,则 在
在 上满足P.S.条件。
上满足P.S.条件。
证 设 且
且 有界,则存在常数
有界,则存在常数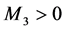 使得对于任意的
使得对于任意的 ,有
,有

由引理3.1的证明,对任意的 ,有
,有

即

由 知,存在
知,存在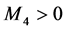 ,使得对任意的
,使得对任意的 ,有
,有

因此,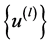 在
在 上有界,从而存在
上有界,从而存在 中的收敛子列,即P.S.条件成立。证毕。
中的收敛子列,即P.S.条件成立。证毕。
定理3.3 的证明我们将利用山路引理来证明定理3.3。由定理3.2,我们已经验证 在
在 上满足P.S.条件。
上满足P.S.条件。
下面验证山路引理的条件 ,
, 。由
。由 有,对
有,对 ,存在
,存在 ,使得当
,使得当 时,
时,
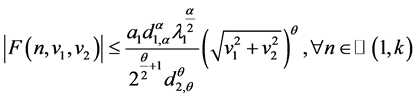
对任意的 和
和 ,有
,有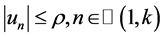 。
。
当 时,
时,

令
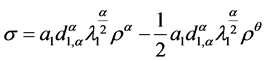
则
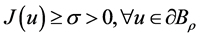
即山路引理的条件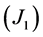 成立。
成立。
显然 ,由P.S.条件的验证过程知
,由P.S.条件的验证过程知
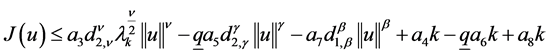
由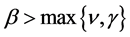 知,当
知,当 充分大时,存在
充分大时,存在 ,使得
,使得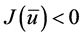 。因此,由山路引理知,至少存在一个临界值
。因此,由山路引理知,至少存在一个临界值 。
。
设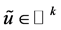 是临界值
是临界值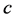 对应的临界点,即
对应的临界点,即 。类似于P.S.条件的验证过程知,对于任意的
。类似于P.S.条件的验证过程知,对于任意的 ,存在
,存在 使得
使得 。显然,若
。显然,若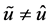 ,证毕。 若
,证毕。 若 ,且
,且 ,由山路引理,
,由山路引理,

其中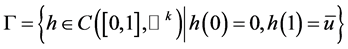 。因此,对于任意的
。因此,对于任意的 ,由
,由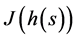 关于
关于 的连续性,
的连续性, 和
和 意味着存在某个
意味着存在某个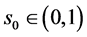 使得
使得 。若选择
。若选择 使得交集
使得交集 是空集,则存在
是空集,则存在 使得
使得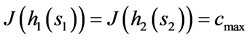 。因此,可得
。因此,可得 中的两个不同的临界点
中的两个不同的临界点 。从而,我们得到
。从而,我们得到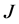 的临界值
的临界值 对应的两个不同的临界点。
对应的两个不同的临界点。
对 ,边值问题(1.1)~(1.2)有下列形式
,边值问题(1.1)~(1.2)有下列形式

在此情况下,很容易完成定理3.3的证明。证毕。
4. 例题
考虑二阶非线性差分方程的边值问题:
对任给的 ,假设
,假设
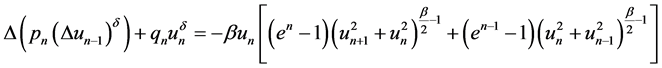 (4.1)
(4.1)
 (4.2)
(4.2)
其中 和
和 是两个实序列,
是两个实序列, 表示正奇数的比,
表示正奇数的比, 。
。
我们有

且
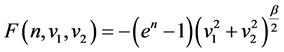
则

易证,定理3.3的所以条件成立,故边值问题(4.1)~(4.2)至少存在两个解。
基金项目
本文得到国家自然科学基金(11571084)资助,在此表示感谢!
文章引用
徐佳琳,周展. 具有超前和滞后的二阶差分方程的边值问题
Boundary Value Problems for Second Order Difference Equations Containing Both Advance and Retardation[J]. 应用数学进展, 2016, 05(04): 695-704. http://dx.doi.org/10.12677/AAM.2016.54081
参考文献 (References)
- 1. Mawhin, J. and Willem, M. (1989) Critical Point Theory and Hamiltonian Systems. Springer-Verlag, New York, 1-498. https://doi.org/10.1007/978-1-4757-2061-7
- 2. Castro, A. and Shivaji, R. (1989) Nonnegative Solutions to a Semilinear Dirichlet Problem in a Ball Are Positive and Radially Symmetric. Communications in Partial Differential Equations, 14, 1091-1100. https://doi.org/10.1080/03605308908820645
- 3. Cai, X.C. and Yu, J.S. (2007) Existence theorems of periodic solutions for second-order nonlinear difference equations. Advances in Difference Equations, 2008, Article ID: 247071. http://advancesindifferenceequations.springeropen.com/articles/10.1155/2008/247071
- 4. Chen, P. and Fang, H. (2007) Existence of Periodic and Subharmonic Solutions for Second-Order p-Laplacian Difference Equations. Advances in Difference Equations, 2007, Article ID: 042530. http://link.springer.com/article/10.1155/2007/42530
- 5. Guo, Z.M. and Yu, J.S. (2003) Existence of Periodic and Subharmonic Solutions for Second-Order Superlinear Difference Equations. Science in China Series A: Mathematics, 46, 506-515. http://link.springer.com/article/10.1007/BF02884022 https://doi.org/10.1007/BF02884022
- 6. Guo, Z.M. and Yu, J.S. (2003) The Existence of Periodic and Subharmonic Solutions of Subquadratic Second Order Difference Equations. Journal of the London Mathematical Society, 68, 419-430. http://xueshu.baidu.com/s?wd=paperuri:(cee5d37083423c7c09e6d275ca20b61f)&filter=sc_long_sign&sc_ks_para=q%3DThe+Existence+of+Periodic+and+Subharmonic+Solutions+of+Subquadratic+Second+Order+Difference+Equations&tn=SE_baiduxueshu_c1gjeupa&ie=utf-8&sc_us=1214 https://doi.org/10.1112/S0024610703004563
- 7. Yu, J.S. and Guo, Z.M. (2006) Boundary Value Problems of Discrete Generalized Emden-Fowler Equation. Science in China, 49, 1303-1314.http://link.springer.com/article/10.1007%2Fs11425-006-1999-z https://doi.org/10.1007/s11425-006-1999-z
- 8. Yu, J.S., Guo, Z.M. and Zou, X.F. (2005) Periodic Solutions of Second Order Self-Adjoint Difference Equations. Journal of the London Mathematical Society, 71, 146-160. https://doi.org/10.1112/S0024610704005939 https://www.researchgate.net/publication/228378772_Periodic_solutions_of_second_order_self-adjoint_difference_equations
- 9. Liu, X., Zhang, Y.B., Shi, H.P., et al. (2013) Boundary Value Problems of Second Order Nonlinear Difference Equations with Jacobi Operators. Journal of Contemporary Mathematical Analysis, 48, 273-284. http://link.springer.com/article/10.3103/S1068362313060046 https://doi.org/10.3103/S1068362313060046
- 10. Liu, X., Zhang, Y.B. and Shi, H.P. (2015) Nonexistence and Existence Results for a Fourth-Order p-Laplacian Discrete Mixed Boundary Value Problem. Mediterranean Journal of Mathematics, 12, 419-432. http://link.springer.com/article/10.1007/s00009-014-0402-5 https://doi.org/10.1007/s00009-014-0402-5
- 11. 石海平. 非线性差分方程的同宿轨、周期解与边值问题[D]: [博士学位论文]. 长沙: 湖南大学, 2009.
- 12. 石海平, 王智刚. 二阶p-Laplacian差分方程的边值问题[J]. 辽宁师专学报: 自然科学版, 2010, 12(1): 1-3.
- 13. Shi, H.P. (2014) Periodic and Subharmonic Solutions for Second-Order Nonlinear Difference Equations. Journal of Applied Mathematics & Computing, 48, 157-171.http://link.springer.com/article/10.1007%2Fs12190-014-0796-z https://doi.org/10.1007/s12190-014-0796-z
- 14. Cai, X.C. (2005) An Existence Theorem for Second Order Discrete Boundary Value Problems. Mathematics in Economics , 320, 649-661.http://en.cnki.com.cn/Article_en/CJFDTotal-JJSX200502017.htm
- 15. Rabinowitz, P.H. (1986) Minimax Mathods in Critical Point Theory with Applications to Differential Equations. CBMS. AMS, New York, 1-156. https://doi.org/10.1090/cbms/065/01