Advances in Applied Mathematics
Vol.07 No.01(2018), Article ID:23616,11
pages
10.12677/AAM.2018.71016
Simulation of Fractal Plant Based on Iteration Function System
Caiyun Li, Hongchan Zheng, Zengyao Lin
Department of Applied Mathematics, Northwestern Polytechnical University, Xi’an Shanxi

Received: Dec. 23rd, 2017; accepted: Jan. 23rd, 2018; published: Jan. 30th, 2018

ABSTRACT
In this paper, based on the introduction of the basic theory of Iterative Function System(IFS), the first application of IFS code to a given image can reveal the shrinkage characteristics of internal affine transformation. The influence of the numbers and parameters of affine transformations on the generation of fractal tree is analyzed. Thus it can generate fractal trees with different morphologies by modifying the IFS code. Using pseudo-affine transformation to achieve the interpolation of the attractor image, the triangular maple leaves and the pentagon maple leaves are generated. Meanwhile, controllable fractal leaves can be obtained through adjusting interpolation points. Finally, some examples of fractal images are given with Matlab.
Keywords:Fractal, Plant Simulation, Pseudo-Affine Transformation, Maple Leaves
基于迭代函数系统的分形植物模拟
李彩云,郑红婵,林增耀
西北工业大学理学院,陕西 西安
收稿日期:2017年12月23日;录用日期:2018年1月23日;发布日期:2018年1月30日

摘 要
本文在介绍迭代函数系统(IFS)基本理论的基础上,根据IFS码对给定图像的第一次应用来揭示内部的仿射变换收缩特性,分析了仿射变换个数以及参数对生成分形树的影响,从而修改IFS码,生成了具有不同形态的分形树。利用拟仿射变换实现吸引子图像的插值,并生成三角枫叶、五角枫叶等,通过调整插值点生成形状可控的分形树叶。最后,结合Matlab给出分形图的若干实例。
关键词 :分形,景物模拟,拟仿射变换,枫叶

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自然景物模拟是计算机图形学中一个重要研究课题,其中植物形态仿真模拟引起了广泛的关注。许多学者对其进行了大量的研究,目前常见的方法有L-系统 [1] [2] 、迭代函数系统 [3] [4] [5] 、粒子系统 [6] [7] 、扩散受限凝聚(DLA)模型 [8] 等。迭代函数系统(Iteration Function System,简称IFS)是绘制植物分形图的主要方法,利用该方法既可以模拟自然界存在的物种也可以创造新物种。1999年郝小琴 [9] 提出了基于树木的分枝模式与叶序模式的三维IFS建模法并生成了槐树和雪松。2004仲兰芬、王琰等 [10] 给出了生成单轴分枝和合轴分枝两类树木的递归算法。2008年潘陆益 [11] 提出了基于IFS的分形图的拟仿射变换模型。2012年韩江萍、周敏等 [12] 利用拟仿射变换实现树木成行、树木成林。2016年仲兰芬、王文忠等 [13] 提出了一种通过包含边缘轮廓和主叶脉的树叶草图生成三维树叶的方法。在利用迭代函数系统生成植物的过程中,大多数文献是直接给出IFS码,鲜有文献分析IFS码中各参数对分形图生成的影响。本文通过IFS码对给定图像的第一次应用来揭示内部的仿射变换收缩特性,分析了各仿射变换参数对分形图的影响效果,根据需求可以人为地设定仿射变换的个数以及参数继而得到相应的IFS码,生成单轴、合轴以及树冠的个数不同的分形树。通过IFS码生成的分形图的拟仿射变换即对分形图的平移、旋转、缩放、错切等变换生成具有相似性的多片叶瓣的树叶如三角枫叶、五角枫叶等。
2. 预备知识
仿射变换是指在不同的方向上变化的比率可以不同的一种比例变换。使一个图形产生它的复制品,于是可以将原图分解为几个部分,每个部分可看作是在不同仿射变换下的复制品,而这种分解与尺度无关,即原图经仿射变换后仍可对其局部图形进行类似的分解,这种整体与局部相似的性质正是分形的特征。
定义1 [8] :变换 具有形式为
其中 为实数,则称 为一个(二维)仿射变换。
当 时,上式常改写为
其中 。
定义2 [8] :度量空间 上的变换 称为压缩映射或压缩,如果存在一常量 ,使得
数 称为 的压缩因子。
定义3 [8] :(迭代函数系统IFS)一个迭代函数系统由一个完备度量空间 和一个有限的压缩映射集 及相应的压缩因子 所组成,每个 有一个伴随概率 且 。迭代函数系统IFS记为: ,随机迭代函数系统IFSP记为: ,且其压缩因子都是 。IFS若满足条件 ,则称之为一个IFS码。
定理1 [8] :设 是拥有压缩因子 的IFS码,则定义变换 为
且 是完备空间 上具有压缩因子 的压缩映射,即
它的唯一不动点集 满足
且 。不动点集 被称为IFS的吸引子。
定理2 [14] :(拼贴原理)设 为度量空间,给定 和 ,选定一个IFS ,其压缩因子 ,使得 ,则有 。这里, 是该IFS的吸引子, 为Hausdorff距离。
3. 不同形态分形树的生成
利用IFS方法生成分形图的关键是找出其相应的IFS码,即仿射变换的系数。下面就介绍仿射变换的一些概念,从而更好地确定IFS码。
3.1. 简单的变换
图形的基本变换包括平移变换、缩放变换、旋转变换、反射变换、错切变换等。利用仿射变换进行分形模拟往往需要连续进行多次基本变换,将整体图形映射为局部图形,称之为组合变换或连续变换。仿射变换对一个图像的第一次应用,通常会揭示其内部的仿射线性收缩特征 [15] 。但是我们还必须注意到,选择一个具有合适结构的图像是非常重要的,只有这样才能够鉴别出其独特的变换,不然就不能够确切地检测出一些可能发生了的旋转和反射。在本文剩下的这些图像中,我们都代表性地使用一个在左上角
镶嵌了一个“L”的 单位正方形作为初始图像。图1给出了图形的4个基本变换。
仿射变换是由6个系数所决定的,为了更方便地探讨压缩变换。将矩阵 改写为以下形式:
只须令
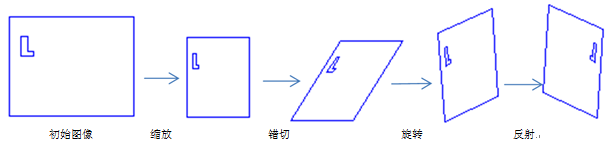 初始图像 缩放 错切 旋转 反射
初始图像 缩放 错切 旋转 反射
Figure 1. Basic transformation of graphics
图1. 图形的基本变换
即可,用类似的式子可以得到 和 。其中 分别表示沿 轴方向缩放的倍数, 分别表示 轴逆时针方向的旋转角度。因此对于任意一个仿射变换都可以用 来表示。
3.2. 分形树的算法实现
上一小节已经介绍了各参数的意义,当给定对应的参数值就可以得到每个仿射变换的系数,而每一个仿射变换被调用的概率不一定相同,随机迭代函数系统 绘制IFS吸引子的实质是按照概率来选择不同仿射变换,即落入图形各部分中点的数目不一定相同。其中:
一般情况下, 由下式给出 [16] :
其中 为第 个仿射变换的系数。
本文采用随机迭代算法,通过Matlab提供的随机数rand(),用随机生成的概率选择一个仿射变换 作为迭代规则迭代一次,不断重复此迭代过程,产生的极限图形就是所要绘制的分形图形。设计的算法步骤如下:
(1) 定义IFSP为 ,设定初始点 和迭代次数 ;
(2) 利用rand()函数生成在区间 的随机数 ,以概率 选取仿射变换 ;
(3) 以 作用点 ,得到新坐标 ;
(4) 令 并在屏幕上打出 ;
(5) 重返第(2)步,进行下一次的迭代,直到迭代次数大于 为止。
下面就根据IFS对给定图像的第一次应用来揭示内部的仿射变换收缩特性,从而调整已有的IFS码中仿射变换的参数,生成形态各异的分形树。
在图2中,图b~图e是在a的基础上修改IFS码中参数得到的图像,a图对应的IFS码见附录的附表1。图b,图c是修改IFS码中的参数 生成的,从第一行可以看出,b图的旋转角度相对于a图变小,从而生成的树各枝干较紧凑,相反地,c图是旋转角度变大,从而生成的树枝干较分散。图d,图e是修改IFS码中的参数 生成的,其中图d是增大 轴的缩放系数 ,生成树的枝干较笔直,图e是增大 轴的缩放系数 ,树枝较弯曲。
在此基础上,我们还可以通过修改仿射变换的个数来改变分形树的形态。在图3中图a通过3个仿射变换生成嫩枝,图b用4个仿射变换生成了枝干繁多的单轴 [10] 分形树,图c用5个仿射变换生成一棵
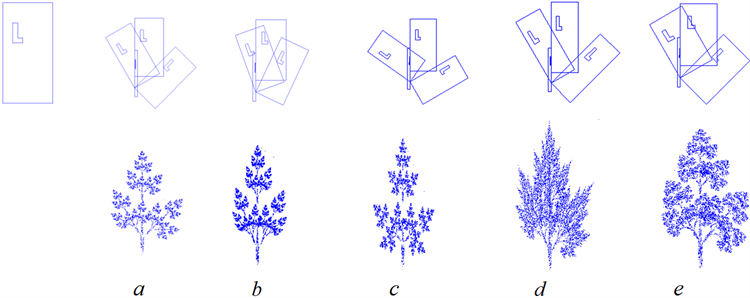
Figure 2. Fractal trees of affine transform with different parameters. The first figure of the first line is the given original image, the last five figures are the images after the first affine transformation of the initial image, and the second line corresponds to the attractor of the IFS code
图2. 仿射变换不同参数的分形树。第一行第一个是给定的原始图像,后面五个是对初始图像经过一次仿射变换的图形,第二行对应IFS码的吸引子
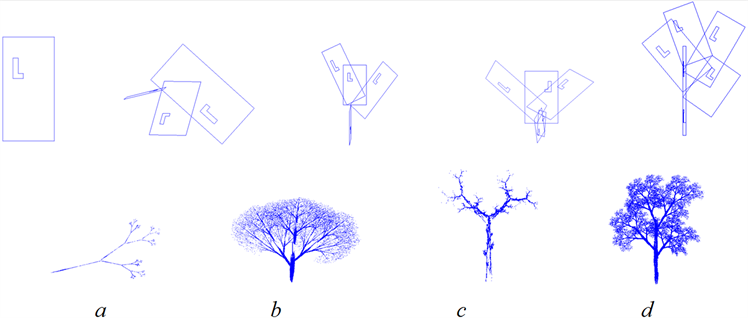
Figure 3. Fractal trees of affine transform with different numbers. The first figure of the first line is the given original image, the last four figures are the images after the first affine transformation of the initial image, and the second line corresponds to the attractor of the IFS code
图3. 仿射变换个数不同的分形树。第一行第一个是初始图像,后面四个是对初始图像经过一次仿射变换的图形,第二行是对应IFS码的吸引子
合轴 [10] 的枯树,图d用6个仿射变换生成具有4个树冠枝叶 [3] 的分形树,图a~图d的IFS码分别对应于附录的附表2~附表5。
我们分析了仿射变换的个数以及相应参数对分形树形状的影响,因此可以根据 来调整树枝之间的紧凑程度, 调整树枝的笔直和弯曲程度,还可以通过仿射变换个数及拼贴方法来决定树的形状,单轴、合轴以及树冠的个数。该方法的优势是利用第1级的映射可以直观地预测分形树的形状,根据我们的需要可以人为地设定仿射变换的个数以及相应的参数,从而得到IFS码并生成对应的分形树。
在自然界中,我们经常会看到具有多片叶瓣的树叶,例如枫叶、三叶草。若还使用上述方法模拟,一片叶瓣需要3~4个仿射变换,当叶片个数较多时,需要拼贴的仿射变换较多,不方便计算。由于这些叶片一般都具有相似的结构,我们采用拟仿射变换的方法可以有效快速地生成树叶。
4. 采用拟仿射变换生成三角枫叶、五角枫叶
4.1. 拟仿射变换
IFS是以仿射变换为框架,经过迭代生成的,但迭代生成的整体分形图却不能简单地使用几何学上的仿射变换的方法实现。我们将分形图整体平移、缩放、旋转、错切等几何变换称为拟仿射变换。其原因在于分形图是一组仿射变换所确定的不动点集,对这些不动点集的拟仿射变换过程就是使这些不动点集从一个状态换到另一个状态的过程,变换后分形图的结构、状态和点的分布密度仍然受IFS码的控制,即在具体算法中,对迭代生成的点进行平移、旋转、缩放、错切等变换操作之后,必须将变换之前的点作为下一次迭代的初值,从而就可以实现分形图整体的仿射变换。在下节中介绍从分形图的拟仿射变换迭代产生的拟仿射变换模型,进而实现分形图的拟仿射变换。
4.2. 分形图的拟仿射变换
为了描述迭代系统的迭代过程,给出如下记号:
变换矩阵: ,位移矩阵: ,变换后的矩阵: ,初始值: ,则IFS的迭代模型用数学表达式表示为:
用矩阵形式表示为:
(1) 分形图的平移变换
分形图的平移就是将原分形图沿坐标轴移动一个分量,记平移矩阵为 ,
平移变换模型为:
用矩阵形式表示为:
(2) 分形图的旋转变换
如果分形图绕坐标原点逆时针旋转角度为 ,则旋转矩阵为 ,
旋转变换模型为:
用矩阵形式表示为:
(3) 分形图的缩放变换
设在 轴方向的放大或缩小的因子为 ,则缩放矩阵为 ,
缩放变换模型为:
用矩阵形式表示为:
(4) 分形图的错切变换
沿 轴方向的切变系数为 ,则错切变换矩阵为 ,
错切变换模型为:
用矩阵形式表示为:
同理,可以得到沿 轴方向的切变系数为 对应的矩阵形式:
在具体的算法中,将迭代部分用这四个迭代方程替换就可以得到分形图的平移,旋转,缩放,错切变换。这里我们生成具有相似的多片叶瓣的树叶如三角枫叶、五角枫叶。通过对原始的分形图作不同的拟仿射变换,实现分形图的可控性。不妨假设其中一片叶子的顶点坐标为 ,用户指定的插值点为 ,则这两点之间夹角为:
对原分形图进行旋转角度为 的旋转变换,其旋转矩阵为 ,
并计算其长度比为:
在上步的基础上再将原图进行缩放,其缩放矩阵为 ,从而实现分形图的插值。
4.3. 可控枫叶的算法实现
在这一节中我们展示生成枫叶的具体过程,三角枫叶和五角枫叶的叶瓣之间具有相似的结构,在这里用分步处理的方法来生成枫叶。先生成其中一片叶子作为目标枫叶,然后利用拟仿射变换对原图像进行变换从而生成我们想要的图像。这里可控性分为两个部分,一是叶片的个数m,二是插值的控制点位置。下面给出生成m片枫叶的算法步骤:
(1) 给定初始插值点 ;
(2) 用上节给出的随机迭代算法生成目标树叶;
(3) 对目标树叶运用拟仿射变换模型,调用m次旋转变换以及缩放变换。
现取 ,图4给出在三个不同插值点下生成的三角枫叶,其目标枫叶的IFS码见附录的附表6。
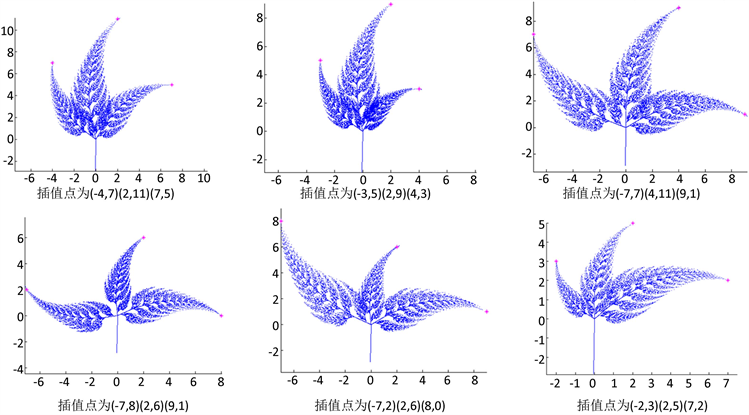
Figure 4. The triangular maple leaves generated by the given three interpolation points
图4. 给定三个插值点生成的三角枫叶

Figure 5. Fractal leaves. The first two figures are triangular leaves by changing the IFS code, and the last two are pentagonal leaves by changing the number of leaves
图5. 分形树叶。前两幅图是改变IFS码的三角叶,后两幅是改变叶子数得到的五角叶
为了使图形更加丰富多彩,可以通过修改IFS码或者改变叶子的个数来生成其他形状的分形叶。在图5中,图a,图b是通过修改IFS码得到的。图c,图d是修改叶瓣数即令 ,其中c图中旋转角度分别为 ,其中d图中旋转角度分别为 。
5. 结论
在利用IFS方法进行树木模拟过程中,通过IFS码对给定图像的第一次应用可以揭示仿射变换的收缩性质,分析了各仿射变换参数对分形图的影响效果,根据需求可以人为地设定仿射变换的个数以及相应的参数继而得到相应的IFS码,生成形态各异的分形树。但在生成具有相似叶瓣的分形树叶的时候,其中的仿射变换个数较多,不易于实现。根据其叶片的相似性,利用拟仿射变换可以实现分形图的平移、旋转、缩放、错切变换,生成了三角枫叶和五角枫叶。通过不同的变换组合方式,可以生成各式各样的图案。
基金项目
陕西省自然科学基础研究计划项目(2016JM6056)。
文章引用
李彩云,郑红婵,林增耀. 基于迭代函数系统的分形植物模拟
Simulation of Fractal Plant Based on Iteration Function System[J]. 应用数学进展, 2018, 07(01): 128-138. http://dx.doi.org/10.12677/AAM.2018.71016
参考文献 (References)
- 1. Prusinkiewicz, P., Hammel, M. and Mjolsness, E. (1993) Animation of Plant Development. Computer Graphics, 27, 351-360.
https://doi.org/10.1145/166117.166161 - 2. Prusinkiewicz, P. and Lindenmayer, A. (1990) The Algo-rithmic Beauty of Plants. Springer-Verlag, New York.
https://doi.org/10.1007/978-1-4613-8476-2 - 3. 李庆忠, 韩金殊. 基于IFS的树木形态模拟方法[J]. 计算机辅助工程, 2004, 13(4): 20-24.
- 4. 肖海蓉. 基于IFS分形算法的树木形态分析和实现[J]. 计算机仿真, 2011, 28(6): 274-279.
- 5. Zhang, H.Q. and Liu, M. (2009) Tree Growth Simulation Method Based on Improved IFS Algo-rithm. International Conference on Computer Intelligence and Software Engineering, 1-5.
https://doi.org/10.1109/CISE.2009.5365658 - 6. 袁琪, 周淑秋, 郭新宇. 粒子系统在虚拟作物生长中的应用研究[J]. 微计算机信息, 2007, 23(21): 262-264.
- 7. 宋万寿, 赖建伟. 基于粒子系统方法的焰火及树木模拟[J]. 计算机辅助设计与图形学学报, 1996, 8(4): 254-258.
- 8. 朱华, 姬翠翠. 分形理论及其应用[M]. 北京: 科学出版社, 2011.
- 9. 郝小琴. 森林景物的三维迭代函数系统建模技术的研究[J]. 计算机学报, 1999, 22(7): 768-773.
- 10. 仲兰芬, 王琰, 程磊. 三维分形树木IFS生成算法[J]. 沈阳理工大学学报, 2005, 24(1): 28-31.
- 11. 潘陆益. IFS分形图拟仿射变换模型及其实现[J]. 计算机系统应用, 2008, 17(1): 83-84.
- 12. 韩江萍, 周敏, 郑红婵, 等. 采用拟仿射变换进行分形树模拟[J]. 计算机工程和设计, 2012, 33(2): 700-704.
- 13. 仲兰芬, 王文忠. 由叶轮廓生成叶脉的树叶建模与绘制[J]. 小型微型计算机系统, 2016, 37(5): 1017-1021.
- 14. 赵健, 雷蕾, 蒲小勤. 分形理论及其在信号处理中的应用[M]. 北京: 清华大学出版社, 2008.
- 15. 海因茨•奥托•佩特根, 哈特穆特•于尔根斯, 迪特马尔•绍柏. 混沌与分形[M]. 北京: 国防工业出版社, 2008.
- 16. 楼顺天, 胡昌华, 张伟. 基于MATLAB的系统分析与设计—模糊系统[M]. 西安: 西安电子科技大学出版社, 2001.
附录
Table 1. Affine transformation parameters of Figure 2(a)
Table 2. Affine transformation parameters of Figure 3(a)
Table 3. Affine transformation parameters of Figure 3(b)
Table 4. Affine transformation parameters of Figure 3(c)
Table 5. Affine transformation parameters of Figure 3(d)
Table 6. Affine transformation parameters of Figure 4
知网检索的两种方式:
1. 打开知网页面http://kns.cnki.net/kns/brief/result.aspx?dbPrefix=WWJD
下拉列表框选择:[ISSN],输入期刊ISSN:2324-7991,即可查询
2. 打开知网首页http://cnki.net/
左侧“国际文献总库”进入,输入文章标题,即可查询
投稿请点击:http://www.hanspub.org/Submission.aspx
期刊邮箱:aam@hanspub.org
