Advances in Applied Mathematics
Vol.07 No.07(2018), Article ID:25987,13
pages
10.12677/AAM.2018.77104
Asymptotic Behavior of Solutions for a Class of Stochastic SIR Models with Virus Mutation
Yi Wang, Jie Ma, Yiqiang Wei
Taiyuan University of Technology, Shijiazhuang Hebei
Received: Jun. 24th, 2018; accepted: Jul. 13th, 2018; published: Jul. 20th, 2018

ABSTRACT
In this paper, we use the Lyapunov analysis method to prove the global existence and uniqueness of a positive solution for a class of stochastic SIR models with virus mutation, and to prove the asymptotic behavior of the solution in the deterministic model of disease-free equilibrium and endemic equilibrium.
Keywords:Stochastic Differential Equations, Lyapunov Analysis Methods, Ito Integration, Global Positive Solution Existence and Uniqueness, Asymptotic Stability
一类带病毒变异的随机SIR模型解的渐近性态
王艺,马洁,魏毅强
太原理工大学,河北 石家庄
收稿日期:2018年6月24日;录用日期:2018年7月13日;发布日期:2018年7月20日

摘 要
本文中,我们利用Lyapunov分析方法证明了一类带病毒变异的随机SIR模型正解的全局存在唯一性,并且证明了其解在确定性模型的无病平衡点和地方病平衡点的渐近性态。
关键词 :随机微分方程,Lyapunov分析方法,伊藤积分,全局正解存在唯一性,渐近稳定性

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 绪论
针对传染病的传播规律及防治方法的研究对人类生活健康及国计民生具有重要意义 [1] 。1927年,Kermack与McKendrick创立了著名的SIR仓室模型,为后来的研究做出了十分巨大的贡献。随后,国内外众多学者在经典的SIR仓室模型的基础上不断地完善修改,建立了大量的数学模型 [2] 。但是上述的这些模型都是确定性模型,然而现实世界中充满了随机性,所以考虑疾病传播过程中的随机因素十分重要,这样就需要建立随机模型来丰富其研究。在随机传染病中,常见的随机干扰的加入方法有以下几种:1) 对系统的参数加入随机扰动;2) 围绕随机传染病模型的正平衡点也就是地方病平衡点作随机扰动;3) 对整个系统加入随机扰动项 [3] 。
本文考虑由于病毒自身产生变异这一随机因素而导致模型的变化,假设全部输入者都是易感者,且感染者分两类:一类是病毒变异前感染者,简称变异前患者;另一类是病毒变异后感染者,简称变异后患者。变异前患者和变异后患者治愈以后变成易感者,但是有部分变异前患者不能治愈从而发展成为变异后患者。变异前患者感染易感者成为变异前患者,变异后患者感染易感者成为变异后患者,疾病的发生率为双线性发生率,且假设其不足以引起致命。由参考文献 [4] 得模型
(1.1)
根据疾病的传播机理,做如下的假设与说明 [5] :
1)
、
、
、
分别表示t时刻易感者的数目,变异前患者数目,变异后患者数目和恢复者数目。
2) 模型表示易感者感染疾病转为染病者而后获得永久免疫后从染病者进入恢复者。
3)
和
分别表示
和
、
和
的传染率系数,且疾病发生率为双线性
。
4) A表示模型的常数输入率,
表示四类人的自然死亡率,
表示变异前患者转变为变异后患者的速率系数,
和
分别表示变异前患者和变异后患者的恢复率系数。参数
都是正常数。
5) 变异前患者的基本再生数为
,变异后基本再生数为
。
在本文中,通过对整个模型加入随机扰动,得到下述随机系统:
(1.2)
其中
是独立标准布朗运动且
为常数是其布朗运动的强度
。
由 [4] [6] [7] 知,当
时,疾病最终将消失,即模型存在着一个无病平衡点
而且这个无病平衡点是全局稳定的;当
时,模型存在使得变异前患者和变异后患者共存的地方病平衡点
且这个点使局部渐近稳定的.在接下来的三章中,我们将通过Lyapunov分析方法分别讨论随机模型(1.2)的正解全局存在唯一性及这个模型解的渐近性态和稳定性。
2. 模型正解的存在唯一性
一般,如果一个随机微分方程对于任何已经给定的初值存在惟一的全局解,也就是说解不发生爆破,那么方程的系数需要满足线性增长和局部Lipschitz两个条件。但是随机模型(1.2)的系数满足局部Lipschitz条件却不满足线性增长条件,所以其解在有限时间内可能发生爆破,故运用Lyapunov分析方法证明该模型的正解是全局存在惟一的 [8] [9] [10] 。
定理2.1:对于任意给定的初值
,当
时,随机模型(1.2)存在惟一的全局解
,并且这个解以概率1位于
中,即对所有的
,有
。
证明:首先模型的系数显然满足局部Lipschitz连续,所以对于任给的初值,模型(1.2)存在惟一局部解
,其中
表示爆破时间.要想证明此解全局存在,只要证明
。第一步,证明
在有限时间内不产生爆破全局存在。设
足够大,使其满足
.
对于每个整数
,定义停时
令
(
表示空集),由停时的定义可知当
时,
是单调递增。令
,显然
有
。若
成立,则有
,因而就证明了
。所以只需证
即可。
利用反证法,如果不是上述结果,那么就存在常数
和
使得
.
则存在整数
使得当
时有
(2.1)
现定义函数
:
(2.2)
注意到下面的结论成立
.
显然函数
是非负的,则对这个函数应用伊藤公式得
(2.3)
其中,
(2.4)
又因为
故有
将结果带入(2.3)得
(2.5)
将上式两边从0到
积分并取期望可得
所以有
(2.6)
令
,则由(2.1)知
。对于每一个
,利用停时的定义可知
这四个之中至少有一个等于m或
,从而便有
所以由(2.6)有
,
其中,
是
的示性函数。令
则有
,矛盾。
所以必有
。这也就意味着
以概率1在有限时间内不会发生爆破。
定理证毕。
3. 随机模型的解围绕确定模型无病平衡点的渐近行为
正如前文所述,当
时,确定性SIR模型(1.1)存在一个无病平衡点
并且是全局稳定的。但是对于随机系统(1.2)
就不再是平衡点了而且
该随机系统的解也不收敛于
。所以本章,将研究随机模型(1.2)的解在
附近的渐近行为。
定理3.1:如果
并且满足下面的条件
(3.1)
则对于任意给定的初值
,模型(1.2)的解是随机稳定的。
证明:首先,做变量代换
,则原模型(1.2)可以写成下述形式
(3.2)
由此可知,
。现定义函数
其中
是待定的常数。显然函数V是正定的,由伊藤公式计算得
(3.3)
其中,
(3.4)
取
,其中
我们又由定理中的条件(3.1)可知
,所以就有
利用完全平方公式有
,将其带入上述不等式可得结果:
所以对于进行变量代换后的模型而言,就证明了模型的零解是随机稳定的。对于原模型而言就是,对于任意给定的初值,模型的解是随机稳定的。
定理证毕。
4. 随机模型的解围绕确定性模型地方病平衡点的渐近行为
本章假设
。此时确定性模型(1.1)存在一个全局渐近稳定的地方病平衡点
,但是这个无病平衡点不是随机SIR模型(1.2)的正平衡点。但是,经研究发现随机SIR模型(1.2)的解的渐近性态是与
有关联的.所以得到下面的定理。
定理4.1:如果
并且满足条件
,那么对于任何给定的初值
,模型(1.2)的解有如下性质
其中,
,
证明:为方便起见,记
,则初始值
。首先,定义一个函数
如下:
(4.1)
其中,
是待定的正常数。
为简便起见,将(4.1)这个函数分成如下两个函数:
,
其中,
由伊藤公式有
和
其中,
(4.2)
和
(4.3)
这里选取
使得
;
使得
。将
的取值带入等式(4.2)中可以得到
那么则有,
如果我们令
,也就是
.又因为定理4.1的条件
,所以就有
因此有
(4.4)
又因为存在不等式:
;
;
;
;
所以将上述不等式带入(4.4)中可以得到
(4.5)
其中有
综上所述,可以得到
将上式两端从0到t积分并且取期望,然后将不等式(4.5)带入其中可得
所以就有
将上式两端除以t并且令
,就可以得到
令
,那么最终得到结论
定理证毕。
该定理证明了模型(1.2)的解在时间均值意义下在无穷远处围绕一个和
有关的定点
做随机振动,震动幅度不超过
。
5. 数值模拟
为了验证前文的结论,我们利用MATLAB软件数值模拟了确定性模型(1.1)和随机模型(1.2)的解。
由图1可知,我们选取的参数满足
时,模型(1.1)仅存在一个无病平衡点
且是全局渐近稳定的。
从图2可以看出,当
,模型(1.1)存在地方病平衡点,并且全局渐近稳定的。地方病平衡点为
。
图1和图3对比有模型(1.2)的解围绕(1.1)的无病平衡点做随机扰动。
图2和图4对比有模型(1.2)的解围绕(1.1)的地方病平衡点做随机扰动。

Figure 1.
,
图1.
,

Figure 2.
,
图2.
,
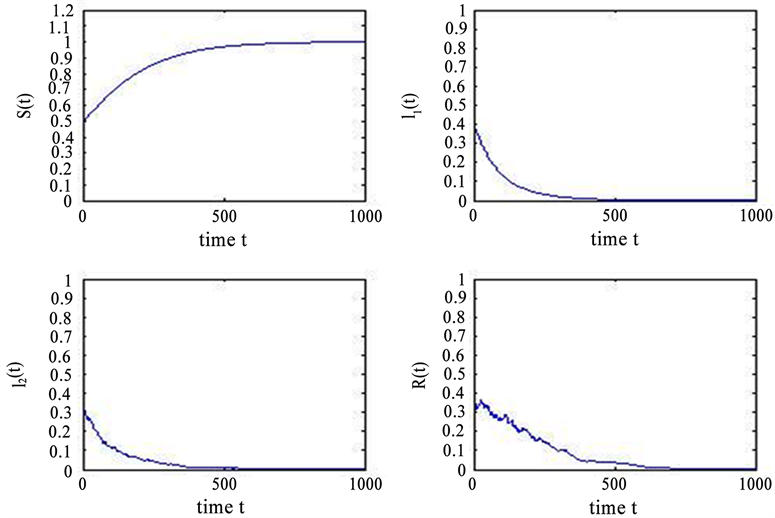
Figure 3.
,
图3.
,

Figure 4.
图4.
6. 总结
本文主要通过Lyapunov分析方法研究了一类带病毒变异的随机SIR模型的解及其渐近性态。首先证明了这个随机模型存在惟一的全局解。其次证明了当确定性模型(1.1)存在无病平衡点时,随机模型(1.2)满足一定的条件时,可以证明其正解将围绕确定性模型的无病平衡点做随机振动。最后证明了当确定性模型(1.1)存在地方病病平衡点时,随机模型(1.2)满足一定的条件时,可以证明其正解将围绕确定性模型的地方病平衡点做随机振动。这些性质在一定程度上揭示了模型的解在一定的条件下是稳定的。
文章引用
王艺,马洁,魏毅强. 一类带病毒变异的随机SIR模型解的渐近性态
Asymptotic Behavior of Solutions for a Class of Stochastic SIR Models with Virus Mutation[J]. 应用数学进展, 2018, 07(07): 863-875. https://doi.org/10.12677/AAM.2018.77104
参考文献
- 1. 马知恩, 周义仓, 王稳地, 靳祯. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004.
- 2. Ma, W., Takeuchi, Y., Hara, T., et al. (2002) Permanence of an SIR Epidemic Model with Distributed Time Delays. Tohoku Mathematical Journal Second, 54, 581-591.
- 3. 于佳佳. 随机传染病模型的渐近性态[D]: [博士学位论文]. 吉林: 东北师范大学, 2010.
- 4. 李海青. 具有常数输入和非线性传染率的传染病模型[D]: [硕士学位论文]. 临汾: 山西师范大学, 2010.
- 5. 李俊. 一类病毒自身发生变异的传染病模型的研究[D]: [硕士学位论文]. 南京: 南京理工大学, 2007.
- 6. Jiang, D.Q. and Shi, N.Z. (2005) A Note on Non-Autonomous Logistic Equation with Random Perturbation. Journal of Mathematical Analysis and Applications, 303, 164-172.
- 7. Mao, X., Marion, G. and Renshaw, E. (2003) Asymptotic Behaviour of the Stochastic Lotka-Volterra Model. Journal of Mathematical Analysis and Applications, 287, 141-156.
- 8. 胡宣达. 随机微分方程稳定性理论[M]. 南京: 南京大学出版社, 1986.
- 9. 龚光鲁. 随机微分方程引论[M]. 北京: 北京大学出版社, 1995.
- 10. Arnold, L. (1972) Stochastic Differential Equa-tions: Theory and Applications. Wiley, New York.