Advances in Applied Mathematics
Vol.
08
No.
05
(
2019
), Article ID:
30564
,
6
pages
10.12677/AAM.2019.85112
Study on Evolution Simulation of Three-Species Food Chain System Considering Spatial Diffusion
Linghui Yu, Zhuang Peng, Luyao Tang
Nanjing University of Science and Technology Institute of Science, Nanjing Jiangsu
Received: May 9th, 2019; accepted: May 24th, 2019; published: May 31st, 2019

ABSTRACT
In this paper, we will study the food chain model of the three species, consider the random migration of each species in space, establish reactive diffusion partial differential equations, and study the evolution of the population through numerical simulation. The qualitative interpretation of the observation results of population evolution is carried out in combination with theoretical analysis.
Keywords:Three Species, Food Chain, Partial Differential Equation, Population Evolution
考虑空间扩散的三物种食物链系统的演化模拟研究
余玲慧,彭妆,汤璐瑶
南京理工大学理学院,江苏 南京
收稿日期:2019年5月9日;录用日期:2019年5月24日;发布日期:2019年5月31日

摘 要
本文我们将研究三物种组成的食物链模型,考虑各个物种在空间中的随机迁移,建立反应扩散型偏微分方程,通过数值模拟来研究种群的演化,并结合理论分析对种群演化的观测结果进行定性的解释。
关键词 :三物种,食物链,偏微分方程,种群演化

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 背景介绍
自然界中的每个物种都不可能单独存在,一定会和其他物种产生相互作用,可能是捕食与被捕食的关系,也可能是相互竞争或者互惠互利的关系。长期以来,研究种群之间的相互作用一直是生态系统的主题之一。19世纪20年代Lotka和Volterra提出了两物种竞争模型(Lotka-Volterra模型),奠定了物种之间相互关系研究的理论基础 [1] [2] 。根据两个种群之间相互作用的形式,可以研究三种情形 [3] :互利共生(两个种群的存在都对对方有利,互相促进增长)、捕食与被捕食(一个物种以另一个物种为食)以及相互竞争(两个种群相互残杀或者竞争同一食物资源的情况,相互抑制增长)。
然而在实际生物种群中,各个物种会随着食物、水分、空间等资源的变化而进行迁移。因此,基于传统的物种演化模型,考虑扩散导致的物种迁移会使得系统更贴近真正的生态系统。目前,国内外学者在考虑空间扩散的两种群相互作用系统中做了大量研究,发现扩散并不总是促进系统的稳定性 [4] [5] 而扩散也不会影响系统的稳定性 [6] [7] 。王茂香老师在研究中发现扩散虽然不影响系统稳定性,但是它改变了系统的演化过程 [8] [9] 。
本文基于文献 [8] [9] 的模型,在三物种食物链模型中考虑空间扩散,建立反应扩散型偏微分方程,通过数值求解偏微分方程,观察种群密度的时空演化,对食物链的保持和断裂进行深入探讨,加深对生态系统演化的理解。
2. 模型建立与分析
考虑具有三个物种的食物链结构,如草原中存在的野兔 → 狐 → 狼的食物链结构:狼以捕食狐为生,狐以野兔为生,狼和狐受食物的限制具有死亡率,而野兔有自己的内禀增长率但是同时也受到环境容纳量的制约。此模型具有十分复杂的动力学现象,包括循环、周期加倍和混沌等行为 [10] 。本文将重点关注物种迁移对系统演化的影响。首先建立反应扩散型偏微分方程:
其中:
t代表时间,x代表空间位移,N1、N2、N3分别是三个物种的种群密度,N1是低级猎物如野兔,N2是中级捕食者如狐,N3是顶级食肉动物如狼。D1、D2、D3分别代表猎物与捕食者的扩散速度。a是猎物种群的内在增长率,b是种内竞争系数,c1是中级捕食者的捕食率,d1表示中级捕食者的死亡率,c2是被吃掉的猎物转化为捕食者的比率,c3是顶级食肉动物的人均捕食率,d2表示顶级食肉动物的死亡率,c4是被吃掉的猎物转化为捕食者的速率,这里的函数f1和f2代表物种间的功能反应函数(表示单位时间内食饵的消耗量)。对模型进行简化:将猎物种群的内在增长率a与种内竞争系数b取值为1,将中级捕食者与食肉动物的死亡率d1、d2都取值为1。
乍一看,扩散是一种随机运动,但由于物种间的相互作用相结合却会产生密度波的传播,即密度波从一个平衡点传播到另一个平衡点,如图1所示。科学家们在理论上研究确实发现对于有扩散的LV模型,通常存在行波解。因此从波传播的角度,可以直接观察系统的稳定性。

Figure 1. The propagation wavefront: (a) wavefront profile obtained by connecting two equilibrium states advances the spatial flow of equilibrium point x to y in. (b) phase plane at velocity c, thus forming a propagation wavefront in (a).
图1. 通过连接两个平衡态得到的传播波前:(a)波前剖面以速度c向前推进。(b)相平面中平衡点x到y的空间流动,从而在(a)中形成传播波面。
首先通过理论计算我们发现系统可能存在四个平衡点: 、 、 、
3. 模拟结果与解释
下面我们将通过数值模拟来研究各个物种密度的演化。本文中常数分别取值为:c1 = 3, c2 = 4, c3 = 3, c4 = 5,得到平衡点的数值解为:P1(0, 0, 0)、P2(1, 0, 0)、P3(0.33, 0.89, 0)、P4(0.5, 0.25, 0.14)。我们发现这个食物链模型具有两个捕食结构,第一级结构是N3捕食N2,第二级是N2捕食N1,从食物链的级次来看,第一级高于第二级。我们将重点关注食物链结构的保持和断裂。
3.1. 食物链的维持
我们知道在传统LV模型中,猎物与捕食者在同一环境下生存,二者的数量随时间周期性的变化。对于考虑扩散的三物种系统,也存在这种常见的情况:即使捕食者比猎物跑得快,它们也只能在同一时空共存,因为物种N3、N2作为捕食者不能在没有猎物的空间里单独生存,如图2所示,此时对应理论上平衡点流向:P4 → P1。
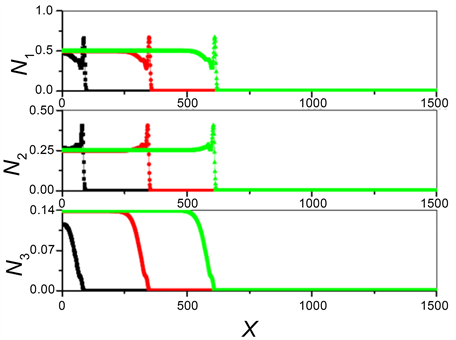
Figure 2. The density of each species evolves with time and space. The black line indicates the evolution of the earliest recorded population with space, while the green indicates that the last recorded population evolves with space, and the red line is between green and black. Parameter selection: c1 = 3, c2 = 4, c3 = 3, c4 = 5; D1 = 1, D2 = 3, D3 = 6
图2. 各个物种密度随时空的演化。黑色线表示最早记录的种群数量随空间的演变,而绿色的表示最晚记录的种群数量随空间的演变,红色线介于绿色与黑色两时刻之间。参数选择:c1 = 3, c2 = 4, c3 = 3, c4 = 5; D1 = 1, D2 = 3, D3 = 6
3.2. 食物链的断裂
低级捕食结构断裂
食物链上的各个物种相互影响,相互制约,一环扣一环。如果某一环节发生“故障”,生态系统就会发生变化。当猎物N1比中间捕食者N2快时第二级捕食结构被打破,猎物可以跑到没有捕食者的空间去,如图3所示平衡点流向P4 → P2出现;此时一级捕食结构仍被保存下来,物种N2与物种N3仍在同一空间中共存。整个食物链系统的平衡点流向为:P4 → P2 → P1。
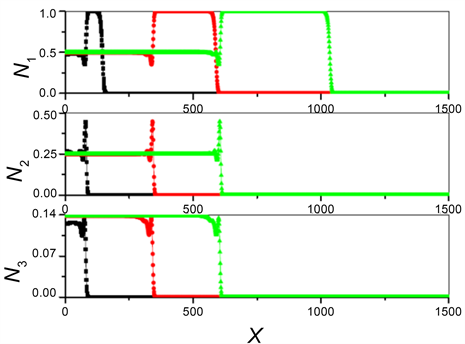
Figure 3. The density of each species evolved with time and space, and the curve was marked with the same figure as figure 2. Parameter selection: c1 = 3, c2 = 4, c3 = 3, c4 = 5; D1 = 3, D2 = 1, D3 = 6
图3. 各个物种密度随时空的演化,曲线标注同图2。参数选择:c1 = 3, c2 = 4, c3 = 3, c4 = 5; D1 = 3, D2 = 1, D3 = 6
高级捕食结构断裂
与相比,两个捕食结构的状态正好相反,此时中间物种N2比它的捕食者物种N3快,猎物N2跑到没有捕食者N3的空间中,此时食物链第一级结构被打破,中间平衡点P3出现;但是二级捕食结构仍被保存下来,物种N1与物种N2在新的空间中共存,只留下高级捕食者N1在原地,由于长期没有食物,最终趋于灭亡,如图4所示。此时整个食物链的平衡点流向为:P4 → P3 → P1。
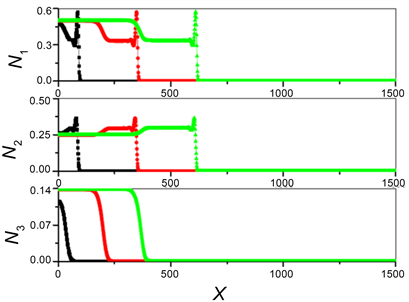
Figure 4. The density of each species evolved with time and space, and the curve was marked with the same figure as figure 2. Parameter selection: c1 = 3, c2 = 4, c3 = 3, c4 = 5; D1 = 1, D2 = 6, D3 = 3
图4. 各个物种密度随时空的演化,曲线标注同图2。参数选择:c1 = 3, c2 = 4, c3 = 3, c4 = 5; D1 = 1, D2 = 6, D3 = 3
食物链完全断裂
传统LV模型中,有猎物就有捕食者,二者共存于一个空间中。但是当考虑物种扩散的时候,猎物可以跑到没有捕食者的空间去,所以当猎物N1比中间捕食者N2跑得快,此时食物链二级结构被打破,猎物N1跑到没有N2的新空间中生存;而顶级捕食者比他俩跑得都慢的时候,物种N2作为一级捕食结构的猎物,高级捕食结构也被打破,如图5所示,此时理论上对应食物链的平衡点流向为P4 → P3 → P2 → P1。
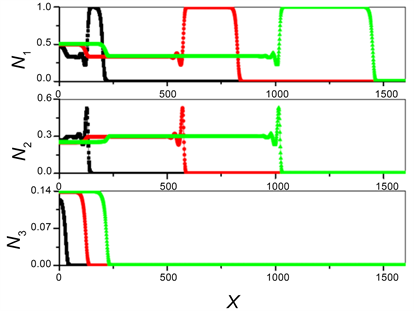
Figure 5. The density of each species evolved with time and space, and the curve was marked with the same figure as figure 2. Parameter selection:c1 = 3, c2 = 4, c3 = 3, c4 = 5;D1 = 6, D2 = 3, D3 = 1
图5. 各个物种密度随时空的演化,曲线标注同图2。参数选择:c1 = 3, c2 = 4, c3 = 3, c4 = 5; D1 = 6, D2 = 3, D3 = 1
4. 总结与展望
本文建立了三物种食物链模型,考虑了各个物种的空间扩散,并通过数值模拟研究了食物链的各种行为:包括食物链的维持以及断裂。在不考虑扩散的传统LV模型中,猎物与捕食者在同一空间中生存,二者的数量随时间周期性变化。而当考虑扩散的时候,猎物和捕食者的迁移能力对食物链系统的演化将产生重要的影响。当捕食者跑得快的时候,捕食者的速度不能无限提升,它会受到猎物速度的限制,保持食物链的运行。但当猎物跑得快的时候,他将可以在没有捕食者的新空间中生存,此时食物链被打破。由于中间物种既是低级捕食结构中的捕食者,又是高级捕食结构中的猎物,它的迁移速度将对食物链的维持和断裂起着关键作用。
通过数值模拟,我们可以直接观察食物链中各物种数量的演化,在理论上找到对应平衡点的流向。但是食物链各种情形变换的临界点在哪里?决定因素有哪些,本文还没有给出解析结果,这些将留待后期进行深入研究。另外对于三物种系统,还有两个捕食者一个食饵,以及两个食饵一个捕食者这两个系统,我们也将作进一步探讨。
致谢
本论文受到南京理工大学本科生科研训练“百千万”计划项目经费资助,项目编号:(201710288031X)。
文章引用
余玲慧,彭 妆,汤璐瑶. 考虑空间扩散的三物种食物链系统的演化模拟研究
Study on Evolution Simulation of Three-Species Food Chain System Considering Spatial Diffusion[J]. 应用数学进展, 2019, 08(05): 984-989. https://doi.org/10.12677/AAM.2019.85112
参考文献
- 1. Lotka, A.J. (1925) Elements of Physiological Biology. Dover Publications, New York.
- 2. Volterra, V. (1926) Fluc-tuation in the Abundance of a Species Considered Mathematically. Nature, 118, 558-560. https://doi.org/10.1038/118558a0
- 3. Zhu, H.Q., Wang, M.X. and Lai, P. (2018) General Two-Species Interacting Lotka-Volterra System: Population Dynamics and Wave Propagation. Physical Review E, 97, 052413. https://doi.org/10.1103/PhysRevE.97.052413
- 4. Vance, R.R. (1984) The Effect of Dispersal on Population Sta-bility in One-Species, Discrete-Space Population Growth Models. American Naturalist, 123, 230. https://doi.org/10.1086/284199
- 5. Allen, L.J.S. (1983) Persistence and Extinction in Lotka-Volterra Reac-tion-Diffusion Equations. Mathematical Biosciences, 65, 1-12. https://doi.org/10.1016/0025-5564(83)90068-8
- 6. Takeuchi, Y. (1986) Bulletin of Mathematical Biology, Vol. 48, 585.
- 7. Hastings, A. (1978) Global Stability in Lotka-Volterra Systems with Diffusion. Journal of Mathematical Biology, 6, 163-168. https://doi.org/10.1007/BF02450786
- 8. Wang, M.-X. and Ma, Y.-Q. (2013) Population Evolution in Mutualistic Lotka-Volterra System with Spatial Diffusion. Physica A, 395, 228-235. https://doi.org/10.1016/j.physa.2013.10.019
- 9. Wang, M.-X. and Lai, P.-Y. (2012) Population Dynamics and Wave Propagation in a Lotka-Volterra System with Spatial Diffusion. Physical Review E, 86, 051908. https://doi.org/10.1103/PhysRevE.86.051908
- 10. Do, Y., Baek, H., Lim, Y. and Lim, D. (2011) A Three-Species Food Chain System with Two Types of Functional Responses. Abstract and Applied Analysis, 2011, Article ID 934569. https://doi.org/10.1155/2011/934569