Advances in Applied Mathematics
Vol.
09
No.
02
(
2020
), Article ID:
34337
,
7
pages
10.12677/AAM.2020.92031
The Difference Scheme of Energy Conservation for the Third Order Linear Equation
Yu Tian, Yanfen Cui
College of Sciences, Shanghai University, Shanghai

Received: Feb. 5th, 2020; accepted: Feb. 20th, 2020; published: Feb. 27th, 2020

ABSTRACT
Based on the third-order linear conservation equation’s many conservation laws, this paper designed a conservation numerical scheme which can satisfy the first two conservation laws of the equation. The numerical examples show the scheme’s effectiveness and the good stability and structure preservation in long-term numerical simulation.
Keywords:Conservation Law, Stability, Structure Preservation

三阶线性方程满足能量守恒的差分格式
田雨,崔艳芬
上海大学理学院,上海
收稿日期:2020年2月5日;录用日期:2020年2月20日;发布日期:2020年2月27日

摘 要
三阶线性守恒型方程具有多个守恒律,本文对该方程设计了一种守恒型数值格式。该格式能满足方程的前两个守恒律。通过数值算例验证了格式有效性,数值结果表明,该格式在长时间的数值模拟中具有很好的稳定性和保结构性。
关键词 :守恒律,稳定性,保结构性

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文对三阶线性守恒方程
 (1)
(1)
进行数值模拟,其中u是方程的解。方程(1)对应的守恒形式为
 (2)
(2)
流函数记为
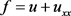 (3)
(3)
方程(1)在物理上,其解满足无穷多个守恒律。本文根据这一物理性质,对这个方程设计一种满足两个守恒律的数值方法。第二个守恒律为
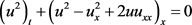 (4)
(4)
其中记 为能量,能量流函数为
为能量,能量流函数为
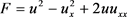 (5)
(5)
在对守恒方程进行数值模拟时,本文采用有限体积法 [1],数值解是对精确解网格平均的逼近,但是与传统有限体积法不同的是,本文设计的数值格式能够满足两个守恒律,格式要求数值解是守恒的,同时要求数值能量也守恒。传统的守恒型数值格式 [2],一般来说只能保持一个守恒律,即使有些格式可以保持多个守恒律,那些守恒律也是被动守恒。本文所设计的格式(见 [3] - [7] )与传统守恒格式不同,该格式同时满足两个守恒律,并且第二个守恒律中的数值实体不是被动守恒,在格式设计中参与计算,即使对线性方程而言,本文的格式也是非线性的。
本文的结构如下,第一节是引言,第二节详细描述了我们的格式,第三节是数值算例,最后是结论。
2. 格式的描述
数值解的定义
本文格式采用均匀网格剖分,网格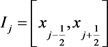 ,
,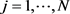 ,其中
,其中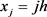 ,
, ,
,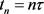 ,在这儿h为空间步长,
,在这儿h为空间步长, 为时间步长。
为时间步长。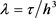 为网格步长比。
为网格步长比。
格式同时计算了两个数值实体,即数值解和数值能量。其中数值解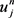 是对
是对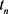 时刻精确解
时刻精确解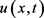 网格平均的近似
网格平均的近似
 (6)
(6)
数值能量 是对
是对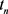 时刻精确能量
时刻精确能量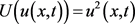 网格平均的近似
网格平均的近似
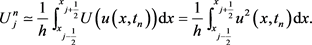 (7)
(7)
如同Godunov型格式一样(见 [1] ),格式分为重构、发展和网格平均三步进行。
第一步重构:在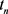 层上对数值解进行重构。由于方程为三阶方程,则重构函数用三次函数重构,重构函数
层上对数值解进行重构。由于方程为三阶方程,则重构函数用三次函数重构,重构函数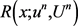 为
为
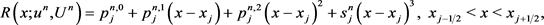 (8)
(8)
其中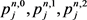 由传统插值方法可得,在这里要求重构函数的网格平均和数值解相等,
由传统插值方法可得,在这里要求重构函数的网格平均和数值解相等,
 (9)
(9)
即重构函数(8)的中的系数在满足(9)式的前提下,由插值可得
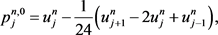 (10)
(10)
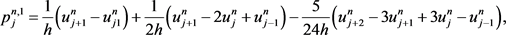 (11)
(11)
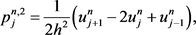 (12)
(12)
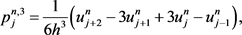 (13)
(13)
与通常插值不同,在重构函数中的三次项系数 作为自由变量,要求重构函数能量的网格平均和数值能量相等,
作为自由变量,要求重构函数能量的网格平均和数值能量相等,
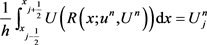 (14)
(14)
由此可见第二个数值实体,即数值能量确实参与格式的计算,因此对于能量来说不是被动守恒。
重构函数三次项系数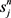 由(14)式可得
由(14)式可得
 (15)
(15)
其中

当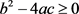 时
时
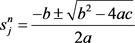 (16)
(16)
其中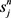 取与
取与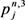 距离近的值。
距离近的值。
当 时
时
 (17)
(17)
第二步发展,以重构函数 作为
作为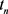 层的初值,求解三阶线性方程
层的初值,求解三阶线性方程
 (18)
(18)
得到精确解 。
。
第三步网格平均,在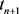 时刻的数值解和数值能量分别为
时刻的数值解和数值能量分别为
 (19)
(19)
 (20)
(20)
对三阶线性方程在 上求二重积分,并应用Green公式可得数值格式为
上求二重积分,并应用Green公式可得数值格式为
 (21)
(21)
 (22)
(22)
其中 是网格步长比。数值流函数和数值能量流函数分别为
是网格步长比。数值流函数和数值能量流函数分别为
 (23)
(23)
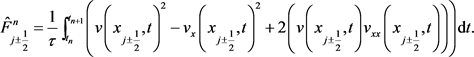 (24)
(24)
在格式中,数值流函数采用左矩形公式数值离散,
 (25)
(25)
数值能量流函数为
 (26)
(26)
3. 数值算例
算例3.1:考虑方程(1),精确解为
 (27)
(27)
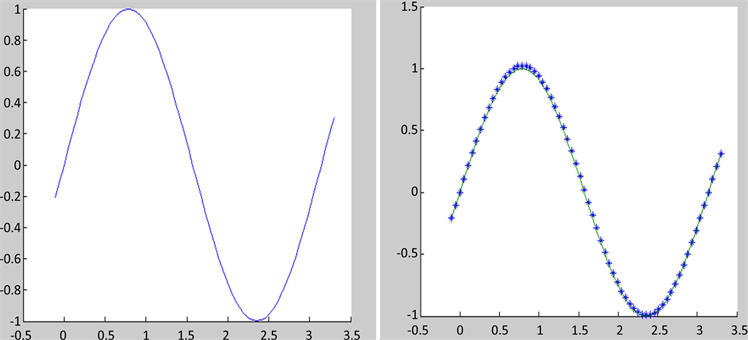
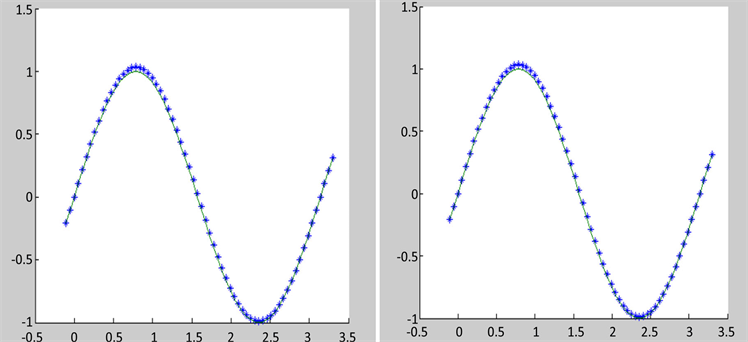
在数值模拟中网格步长比 ,实线表示精确解,*表示数值解,数值结果如图1所示,其中图a是初值图像,图b、图c、图d分别为计算一个周期、十个周期和五十个周期后的结果。
,实线表示精确解,*表示数值解,数值结果如图1所示,其中图a是初值图像,图b、图c、图d分别为计算一个周期、十个周期和五十个周期后的结果。
 (a) (b)
(a) (b)
 (c) (d)
(c) (d)
Figure 1. Numerical results at different times
图1. 不同时刻的数值结果
由此可看出,数值解在50个周期也保持了很好的数值模拟效果,这是因为我们的数值格式满足两个守恒律,所以数值结果在长时间的数值模拟中能保持很好的效果。
算例3.2:考虑方程(1)的双波解
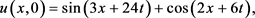 (28)
(28)
在本算例中,考虑两个波为初值,从而可以看出波的干涉的情况,数值结果显示了两个波的干涉过程。
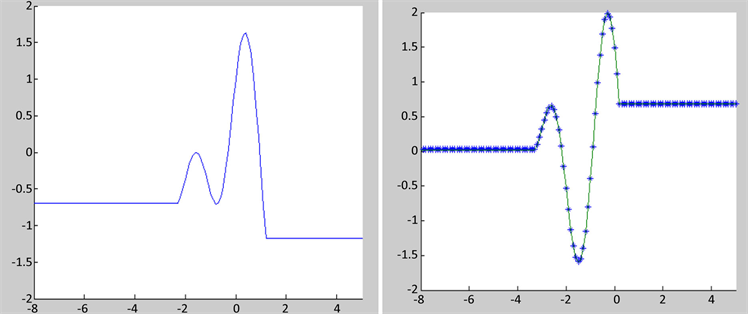
在数值模拟中网格步长比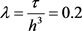 ,结果如图2所示,其中实线代表精确解,*代表数值解,图a表示初始图像。图b、图c、图d分别代表
,结果如图2所示,其中实线代表精确解,*代表数值解,图a表示初始图像。图b、图c、图d分别代表 ,
, ,
, 时刻的数值解。可以看出,在波的干涉过程中,数值解能很好的保持解得结构。
时刻的数值解。可以看出,在波的干涉过程中,数值解能很好的保持解得结构。
 (a) (b)
(a) (b)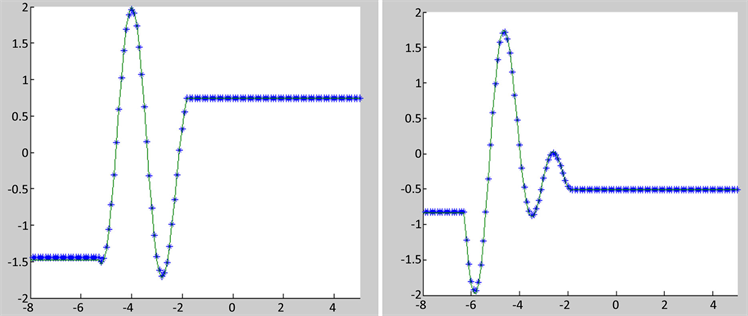 (c) (d)
(c) (d)
Figure 2. Numerical results at different times
图2. 不同时刻的数值结果
4. 结论
对于三阶线性守恒型方程,本文设计了同时满足两个守恒律的差分格式,该格式是通过满足方程物理上的守恒性质得到的,这样的格式具有很好的保结构性质。这种守恒型格式可推广到非线性的守恒方程和高维的方程。
文章引用
田 雨,崔艳芬. 三阶线性方程满足能量守恒的差分格式
The Difference Scheme of Energy Conservation for the Third Order Linear Equation[J]. 应用数学进展, 2020, 09(02): 263-269. https://doi.org/10.12677/AAM.2020.92031
参考文献
- 1. LeVeque, R. J. (2002) Finite Volume Methods for Hyperbolic Problems. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511791253
- 2. Harten, A., Osher, S., Engquist, B. and Chakravarthy, S.R. (1986) Some Results on Uniformly High-Order Accurate Essentially Nonoscillatory Schemes. Applied Numerical Mathematics, 2, 347-377. https://doi.org/10.1016/0168-9274(86)90039-5
- 3. Cui, Y. and Mao, D. (2007) Numerical Method Satisfying the First Two Conservation Laws for the Korteweg-De Vries Equation. Journal of Computational Physics, 227, 376-399. https://doi.org/10.1016/j.jcp.2007.07.031
- 4. 李红霞, 茅德康. 单个守恒型方程熵耗散格式中熵耗散函数的构造[J]. 计算物理, 2004, 21(3): 319-331.
- 5. 李红霞. 一维守恒型方程(组)的熵耗散格式[D]: [博士学位论文]. 上海: 上海大学, 2005.
- 6. 王志刚. 线性传输方程的满足多个守恒律的差分格式[D]: [硕士学位论文]. 上海: 上海大学, 2006.
- 7. 王志刚, 茅德康. 线性传输方程满足3个守恒律的差分格式[J]. 上海大学学报(自然科学版), 2006, 12(6): 588-592+598.