Pure Mathematics
Vol.
08
No.
05
(
2018
), Article ID:
27044
,
5
pages
10.12677/PM.2018.85078
Study on the Product of Two Hyperbolic Iterated Function Systems
Yu Zhao
School of Math and Computer, Guangdong Ocean University, Zhanjiang Guangdong

Received: Sep. 8th, 2018; accepted: Sep. 23rd, 2018; published: Sep. 30th, 2018

ABSTRACT
By using the two known iterated function systems:
and
, this paper constructs the new iterated function system on product space
, which has some similar properties to the lifting dynamic systems and has lots of relations with the two known systems.
Keywords:Hyperbolic Iterated Function Systems, Product Space, Attractor

关于两个双曲迭代函数系的乘积的研究
赵 瑜
广东海洋大学数学与计算机学院,广东 湛江
收稿日期:2018年9月8日;录用日期:2018年9月23日;发布日期:2018年9月30日

摘 要
本文利用两个已知的双曲迭代函数系:
和
,构造积空间
上的迭代函数系,使这个新的双曲迭代函数系具有与升腾动力系统相类似的性质,并且与原来的两个迭代函数系有密切的联系。
关键词 :双曲迭代函数系,积空间,吸引子

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
对于两个已知的双曲迭代函数系
和
[1] ,能否像乘积拓扑空间(见 [2] [3] )一样,以自然的方式构造出在
上的双曲迭代函数系,使得所构造出的双曲迭代函数系不能太平凡,并应与原来两个迭代函数系有很多内在的联系(见 [2] [3] ),因乘积拓扑和有很多联系,却比它们的结构复杂,所以,
上的双曲迭代函数系一定比X上的双曲迭代函数系和上的双曲迭代函数系复杂,对此问题的研究至此未见讨论。
度量空间
与定义在其上的一有限个压缩映射族
,组成一个双曲迭代函数系,用IFS表示它,记为
;如果
的压缩比为
,则称
为此IFS的压缩比(见 [1] [4] [5] [6] )。
设
是完备度量空间
上的双曲迭代函数系,其压缩比为c,变换
,由下式定义:
,则W是分形空间
上压缩比为c的压缩映射,且存在唯一的不动点(不变集)
,满足:
且对
,都有
(见 [1] [3] [4] [5] [6] )。
不动点
称为此IFS的吸引子(见 [1] [3] [4] [5] [6] )。
2. 若干引理
引理2.1(见 [2] [3] )设
是度量空间,则它们的度量积空间
是把
作为拓扑空间时的积空间,其中:
。
引理2.2(见 [2] [3] )设
是两个度量空间,定义:
,其中
,
则d与
是等价的度量。
引理2.3 [2] 若集合上的两个度量
和
是等价的,则X的子集A是度量空间
中的开集当且仅当A是度量空间
中的开集。
以上三个引理的证明极易,故从略。
引理2.4 [2] 设
是两个完备度量空间,则
也是完备度量空间,其中d是按引理2的方式来定义。
证明:由引理2.1知
是度量空间,设有一柯西序列
,则对
,总存在自然数N,使得当
时,有
,
所以
是X中的柯西序列,
是Y中的柯西序列,有X和Y的完备性知,
和
均存在,记
,因此
。
3. 主要结果
定理3.1:设
是两个完备度量空间,
和
是两个双曲迭代函数系,
压缩比为
,
的压缩比为
,令
,则
是完备度量空间
上的双曲迭代函数系。
证明:由于
所以
是压缩映射,
。由引理4知
是完备的,因此定理得证。
称定理3.1中的双曲迭代函数系
为双曲迭代函数系
和
的乘积。
关于两个迭代函数系的乘积,有以下的性质:
定理3.2:(影象定理),设A是完备度量空间上的双曲迭代函数系
的吸引子,B是完备度量空间上的双曲迭代函数系
的吸引子,则
是这两个IFS的乘积的吸引子;反之,C是这两个IFS乘积的吸引子,则
是
的吸引子,
是
的吸引子,其中
为自然投影。
证明:1)
,
,则
。于是定理的前半部分得证。
2)
,其中
和
同(1)中的定义,则
,从而
,又由于
,所以
,
因而有:
,同理可证得:
。由于吸引子是唯一的不动点,所以有
。
注记3.1:定理3.2的证明,用到以下的结果:
。事实上,设
,则
;反之,若
,则有
为
的紧子集且非空,即
。
注记3.2:
与
的乘积的压缩比是两IFS的压缩比的最大值。
注记3.3:以上的定理及定义,可推广到任意有限多个的情形。
定理3.3设
是两个完备度量空间,
和
是两个双曲迭代函数系,他们的乘积为:
则有:
1)
是全不连通的当且仅当
与
都是全不连通的。
2)若
是刚触及的,则在两个曲线迭代函数系
与
中,至少有一个也是刚触及的。
3)
与
均是刚触及的,则
也是刚触及的。
证明:设A是
的吸引子,B是
的吸引子,则
是完备度量空间
上的
IFS:
的吸引子,于是有:
,其中
,同时要求
以字典顺序关系作为此集合的偏序关系,
,
为自然投射,所以有:
,由引理5知:
存在,且
与
的选择无关以及
是连续满射。
1) 若
是
全不连通的,则
是单点集,由于
,其中
所以
,其中:
则
是单点集当且仅当
和
也是单点集,因此结论(1)得证。
2) 由1)知
不是全不连通的当且仅当
或
不是全不连通的。若
是刚触及的,则存在非空开集
,使得:
①
;
②
;
由①有
,所以
或者
,又
,若
,则
,有
,而
是X中的非空开集,同理可证得
,
,
,且
为中的非空开集。
由②有
,所以有
,并且也有
,因此
或
是刚触及的。
3)
和
是刚触及的,由1)可知:
不是全不连通的,且存在一个非空开集
,使得:
①
,
,有
;
②
,从而
,
(因为也存在非空开集
,使得:③
,
,有
;④
),显然
且
是
中的非空开集,因此结论得证。
推论3.1 设
是两个完备度量空间,
与
是两个双曲迭代函数系,则有
1) 若
与
是重叠的,则它们的乘积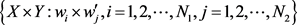 也是重叠的。
也是重叠的。
2) 若
是重叠的,则
是重叠的,或者
是重叠的。
证明:1) 由定理3.3中的1)可知
不是全不连通的,再由定理3.3中的2)知
不是刚触及的,因此结论得证。
2) 由定理3.3中的1)可知,
与
都不是全不连通的,再由定理3.3中的3)知结论成立。
文章引用
赵 瑜. 关于两个双曲迭代函数系的乘积的研究
Study on the Product of Two Hyperbolic Iterated Function Systems[J]. 理论数学, 2018, 08(05): 584-588. https://doi.org/10.12677/PM.2018.85078
参考文献
- 1. 曾文曲, 王向阳, 孙炜, 刘丹, 王福龙. 分形理论与分形的计算机模拟(修订版) [M]. 沈阳: 东北大学出版社, 2001.
- 2. 熊金城. 点集拓扑讲义(第二版) [M]. 北京: 高等教育出版社, 2001.
- 3. 谢和平, 薛绣谦. 分形应用中的数学基础与方法[M]. 北京: 科学出版社, 1997.
- 4. 王兴元. 广义M-J集的分形机理[M]. 大连: 大连理工出版社, 2002.
- 5. 严珍珍, 杨润生. 树上乘积自映射周期点集的局部度量稳定性[J]. 系统科学与数学, 2004, 24(1): 35-40.
- 6. Barnsley, M.F. and Demko, S.G. (1985) Iterated Function Systems and the Global Construction of Fractals. The Proceedings of the Royal Society, A399, 243-275.







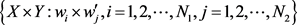 也是重叠的。
也是重叠的。