Pure Mathematics
Vol.
08
No.
06
(
2018
), Article ID:
27816
,
6
pages
10.12677/PM.2018.86095
Study on Steady-State Performance Measures of the Gt/Gt/1 Queue Model
Junxia Wang, Jianmin Liu, Qianqian Wei
Department of Mathematics, Chang’an University, Xi’an Shaanxi
Received: Nov. 6th, 2018; accepted: Nov. 23rd, 2018; published: Nov. 30th, 2018

ABSTRACT
For the Gt/Gt/1 single-server queue model with time-varying arrival rate, we suppose that the waiting space is infinite. By combining the knowledge of the Stochastic-Process Limit and the Convergence of Probability Measures, then the convergence limits of the steady-state performance measures in the queue model are obtained on the basis of a given arrival rate function.
Keywords:Steady-State, Single-Server Queue, Brownian Motion, Convergence Limit
Gt/Gt/1队列模型稳态性能指标的研究
王军霞,刘建民,尉茜茜
长安大学理学院,陕西 西安
收稿日期:2018年11月6日;录用日期:2018年11月23日;发布日期:2018年11月30日

摘 要
针对到达率随时间变化的单服务台Gt/Gt/1队列模型,假定等待空间无限,在给定到达率函数的基础上,应用随机过程极限和概率测度收敛的相关知识,得到该队列模型各稳态性能指标的收敛极限。
关键词 :稳态,单服务台队列,布朗运动,收敛极限

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
排队论主要研究各种排队系统在排队等待中的概率特性,应用领域非常广泛,国内外学者针对不同的排队模型做了大量的研究。Ward通过奥伦斯坦–乌伦贝克过程,得到了稳态下单服务台队列的扩散逼近 [1] 以及负荷过程和队长过程的收敛极限 [2] 。文献 [3] [4] 研究了高负荷下单服务台队列的队长和溢出过程的极限。在高负荷条件下,Liu等研究了到达率随时间变化的网络队列模型 [5] ,Whitt研究了到达临界点的单服务台队列 [6] 。另外,Ma [7] 和Dong [8] 分别对单服务台和多服务台的周期到达队列模型做了一定的研究,并对模型进行数值模拟,更加直观地验证了所得结论。Baccelli等 [9] 和Stanford [10] 在平稳状态下研究了一个服务台的队列性能,得到了有关数量分布的积分方程。本文在前人研究的基础上,运用中心极限定理以及连续映射定理等 [11] [12] 相关知识,研究到达率随时间变化的Gt/Gt/1队列模型,得到队列模型的各种性能指标(到达过程、队长过程和虚等待时间)的收敛极限。
2. Gt/Gt/1队列模型
考虑一般的单服务台Gt/Gt/1队列模型,假定等待空间无限,到达率随时间变化,到达率为 ,服务率为 ,负荷强度为 。A表示到达计数过程, 表示累积到达函数,当 时,
,
到达率满足:
,
在不考虑顾放弃的情况下,假设 。
到达过程满足:
,
其中 是随机计数过程,满足泛函强大数定理(FSLLN)和泛函中心极限定理(FCLT),即当 时,在D空间中,
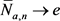 ,
,
,
,
这里 , ,e是恒等函数, , 是标准的布朗运动。
另外,假设服务是由随机计数过程 (独立于 )产生的, 同样满足泛函强大数定理(FSLLN)和泛函中心极限定理(FCLT),即当 时,在D空间中,
, 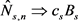 ,
,
这里 , , 是标准的布朗运动,且独立于 。
3. 主要结论及讨论
考虑一系列模型中的第n个模型,下面建立与到达过程有关的高负荷极限,对于单服务台的高负荷极限,通常使负荷强度逐渐趋于1,这里当 时,令 。当 、 时,对到达函数 和累积到达函数 进行流体刻画,分别为:
, .
则有 。
另外,为了后续研究的方便,对累积到达函数 在时间 通过增量 进行刻画,即 ,当 时,有:
, , .
假设在D空间中,当 时, , 。
累积到达函数 的扩散刻画如下
,
假设 , 为连续函数。
到达过程满足:
,
根据以上到达函数的刻画,接下来对到达过程进行刻画,如下:
, ,
, , .
定理1 (到达过程的极限):在以上刻画的前提下,在D空间中,当 时,
有如下的泛函强大数定理: 。
以及泛函中心极限定理: ,
.
证明:根据文献 [11] 中13.2以及连续映射定理,
且由 , ,得
,
又由 , ,得:
由 ,以及胎紧性,有: ,进而得:
接下来刻画队长和虚等待时间:
当 时, , 。
是漂移系数为a,扩散系数为b的反射布朗运动。
定理2 (虚等待时间的高负荷极限):假定系统开始为空,在以上刻画的基础上,且满足以上到达函数,则在
空间中,当
时,有
,这里当
时,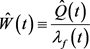 ,
,对于每一个
,
,对于每一个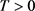 ,当
,当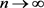 时,
时,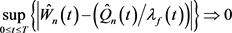 。
。
证明:首先刻画到达和服务过程,当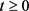 、
时,
、
时,
,
,
所以当
时,在 空间中,
空间中,
,
其中 和 是相互独立的布朗运动,
因此在D空间中, ,
其次应用 [11] 中的定理9.3.4以及连续映射定理,当 时,得:
,且 。
代表第n个系统中的离去过程,
,
其中 。
在D空间中,当 时, 。
是 时间内忙的服务台。
,
根据 以及 [11] 中的定理9.3.4,可得:
,
由 , 得 。
由 ,及 , ,得:
对于每一个
,当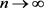 时,
.
时,
.
由联合极限以及 [11] 中的定理11.4.7,得:
在 空间中,当 时,有 。
4. 总结
在给定Gt/Gt/1队列模型的到达率函数的基础上,利用泛函中心极限定理、连续映射定理等得到该模型的到达过程、队长过程和虚等待时间的收敛极限,最后运用概率测度收敛和随机过程极限的知识对此做了证明。
文章引用
王军霞,刘建民,尉茜茜. Gt/Gt/1队列模型稳态性能指标的研究
Study on Steady-State Performance Measures of the Gt/Gt/1 Queue Model[J]. 理论数学, 2018, 08(06): 706-711. https://doi.org/10.12677/PM.2018.86095
参考文献
- 1. Ward, A.R. and Glynn, P.W. (2003) A Diffusion Approximation for a Markorvian Queue with Reneing. Queuing Systems, 43, 103-128.
- 2. Ward, A.R. and Glynn, P.W. (2005) A Diffusion Approximation for a Heavy-Traffic Limits for a GI/GI/1 Queue with Balking or Reneging. Queuing Systems, 50, 371-400.
- 3. Jelenkovic, P.R. (1999) Subexponential Loss Rates in GI/GI/1 Queue with Applications. Queuing Systems, 33, 91-123.
- 4. Whitt, W. (2004) Heavy-Traffic Limits for Loss Proportions in Single-Server Queues. Queuing Systems, 46, 507-536.
- 5. Liu, Y.N. and Whitt, W. (2014) Stabilizing Performance in Networks of Queues with Time-Varying Arrival Rates. Probability in the Engineering and Information Sciences, 28, 419-449.
https://doi.org/10.1017/S0269964814000084 - 6. Whitt, W. (2016) Heavy-Traffic Limits for a Single-Server Queue Leading up to a Critical Point. Operations Research Letters, 44, 796-800.
https://doi.org/10.1016/j.orl.2016.10.005 - 7. Ma, N. and Whitt, W. (2018) A Rare-Event Simulation Algorithm for Periodic Single-Server Queues. Informs Journal on Computing, 30, 71-89.
https://doi.org/10.1287/ijoc.2017.0766 - 8. Dong, J. and Whitt, W. (2015) Using Birth-and-Death Processes to Estimate the Steady-State Distribution of A Periodic Queue. Naval Research Logistics, 62, 664-685.
https://doi.org/10.1002/nav.21672 - 9. Baccelli, F., Boyer, P. and Hebuterne, G. (1984) Single-Server Queues with Impatient Customers. Journal of Applied Probability and Advances in Applied Probability, 16, 887-905.
- 10. Stanford, R.E. (1979) Renging Phenomena in Single Channel Queue. Mathematics of Operations Research, 4, 162-178.
https://doi.org/10.1287/moor.4.2.162 - 11. Whitt, W. (2002) Stochastic-Process Limits. Springer, New York.
- 12. Billingsley, P. (1999) Convergence of Probability Measures. 2nd Edition. Wiley, New York.
https://doi.org/10.1002/9780470316962