Pure Mathematics
Vol.
09
No.
03
(
2019
), Article ID:
30297
,
11
pages
10.12677/PM.2019.93047
Finite Volume Method for a Space Distributed-Order Time-Fractional Diffusion Equation
Yingying Yang, Jing Li*
School of Mathematics and Statistics, Changsha University of Science and Technology, Changsha Hunan

Received: Apr. 25th, 2019; accepted: May 5th, 2019; published: May 20th, 2019

ABSTRACT
In this paper, the space distributed-order time-fractional diffusion equation is considered. We propose a finite volume method to solve the considered equation. Firstly, we use the mid-point quadrature rule to transform the space distributed-order term into a multi-term fractional term, and the multi-term fractional equation is discretized by the finite volume. For the time-fractional derivative, we apply the finite difference method. We prove that the iterative scheme is unconditionally stable and convergent. A numerical example is presented to verify the effectiveness of the proposed method.
Keywords:Space Distributed-Order Equation, Time-Fractional Diffusion Equation, Finite Volume Method, Stability and Convergence
空间分布阶时间分数阶扩散方程的有限体积法
杨莹莹,李景*
长沙理工大学数学与统计学院,湖南 长沙

收稿日期:2019年4月25日;录用日期:2019年5月5日;发布日期:2019年5月20日

摘 要
本文利用有限体积法研究了空间分布阶时间分数阶扩散方程。首先,用中点求积法将空间分布阶项转化为多项空间分数阶项,利用有限体积法对多项空间分数阶项进行离散。而对于时间分数阶导数,我们采用有限差分法。其次,我们证明了迭代格式的无条件稳定性和收敛性。最后通过一个数值例子来证明算法的有效性。
关键词 :空间分布阶方程,时间分数阶扩散方程,有限体积法,稳定性和收敛性

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着科学技术的发展,分数阶微分方程因其在工程、物理、经济学、生物学、医学等诸多领域的应用而受到广泛关注。分数阶微分方程可用来模拟复杂扩散现象,包括反常扩散过程和大范围空间相互作用的扩散过程,而这些过程不能通过传统的二阶扩散方程精确模拟。许多研究表明,与单项、多项时间、空间或时空分数阶微分方程相比,分布阶微分方程更适合用来描述在整个时域内缺乏幂律尺度的加速慢扩散和减速超扩散。在Caputo [1] 首次提出用于非弹性介质应力–应变关系的分布阶微分方程之后,越来越多专家关注如何求解分布阶微分方程。
胡和刘 [2] 研究了一种隐式差分方法去求解一个新的时间分布阶和双侧空间分数阶对流–色散方程。卜等人 [3] 使用加权和移位Grünwald差分方法来研究时间分布阶扩散方程。Yamamoto [4] 研究了一类具有Caputo分数阶导数的时间分布阶扩散方程初边值问题,给出了解析解,并讨论了它在反问题中的应用。刘等人 [5] 提出了一种基于径向基函数的无网格方法来求解时间分布阶对流–扩散方程。也有一些关于研究空间分布阶微分方程的文章。如李和刘 [6] 提出了一种有限体积法求解空间分布阶对流–扩散方程。Jia和Wang [7] 发展了一种快速的有限差分法来求解一般凸域上的空间分布阶偏微分方程。
相比较而言,时间分数阶导数被认为是模拟慢扩散过程的有力工具 [8] ,而空间分布阶方程能灵活地表示介质的作用及其与流体的空间相互作用。因此,本文提出了一种有限体积法求解空间分布阶时间分数阶扩散方程:
, (1)
边界值:
, (2)
初始值:
, (3)
是源项,
是满足下面条件的非负权函数:
,
,
,
.
在通常情况下 [9] ,
可以表示为
。
l和K是正的常数,
,
,
。
定义为Caputo分数阶导数:
.
是Riesz分数阶导数,定义为:
.
其中
,
。
本文提出了一种有限体积法求解空间分布阶时间分数阶扩散方程(1)~(3)。本文的结构如下:第二节,我们应用有限差分近似时间分数阶导数,然后离散空间分布阶方程为一个多项分数阶方程,进而我们使用有限体积法去求解多项分数阶方程,推导出Crank-Nicolson迭代格式。第三节,我们证明了迭代格式的稳定性和收敛性。第四节给出一个数值例子来说明本文数值方法的有效性。
2. 有限体积法求解空间分布阶时间分数阶扩散方程的Crank-Nicolson迭代格式
令
,
,
,
离散区间
,其中
,
。
采用文献 [10] 的离散方法,时间分数阶导数项可以近似为下面格式:
(4)
其中
,
,
。在(1)中,如果
,我们可以得到
. (5)
定义
,
,用网格
离散区间
且
,
,
。用中点求积法,得到
. (6)
结合(1),(4),(6)我们可以得到
(7)
其中
,
,
,
。
定义
,
为区间
的中点。方程(7)在
,
下积分,得到
(8)
现在,我们将空间
定义为网格
上的分段线性多项式的集合。然后,近似解
可以用分段多项式表示为
。
是
的节点基函数。
表示为下面形式:
和
,
因此我们可以得到Crank-Nicolson格式:
(9)
通过直接计算,当
,
,得到
和
其中,
。
因此,方程(9)可以表示为
令
,其中
,
.
因此,当
时,
, (10)
当
时,
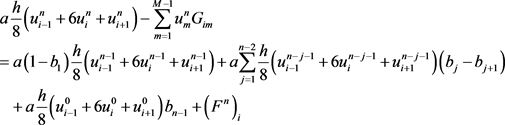 (11)
(11)
其中
,令
,
,
,
,
,
。因此方程(10),(11)可以表示为
(12)
边界值和初始值分别离散为
,其中
,
。
3. 迭代方法的稳定性和收敛性
定理1. 当
时,系数
满足:
,则G是严格对角占优的。
定理2. 当
时,
,B是严格对角占优的,并且
的谱半径满足:
。
证明:
类似与 [6] 定理2的证明,可得该定理的证明。
定理 3. 令
,当 时,如果
或
,则D是严格对角占优的,且
时,如果
或
,则D是严格对角占优的,且
.
证明:
类似与 [11] 定理3的证明,可得该定理的证明。
定理4. 矩阵
的谱半径满足
。
证明:类似与 [11] 定理4的证明,可得该定理的证明。
定理5. 假定
和
分别为差分格式(12)的近似解和数值解且
,
,则
,因此差分格式(12)是无条件稳定的。
证明:现在我们用数学归纳法来证明稳定性。
当
时,将
代入(12),得到
。令
,根据定理4,我们知道
,则存在向量范数和诱导矩阵范数
,使
。使用以上范数,得到:
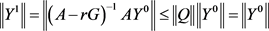 .
.
假设当
时,成立
。
则当
时,由文献 [12] 可知
。因此
得到
,定理证毕。
定理6. 假定
为(1)~(3)的精确解,则当
,
和h趋近于零时,数值解
无条件收敛到精确解
,并且,
.
其中
,
.
证明:设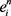 为点
处的误差。将
代入(10)和(11),并结合(7)和文献 [13] 的引理3,推论1,得到:
为点
处的误差。将
代入(10)和(11),并结合(7)和文献 [13] 的引理3,推论1,得到:
其中
,
,且矩阵形式为:
.
下面,我们用数学归纳法来证明这个定理。
当
时,得到
.
根据定理2和定理4已知
,
,则存在向量范数和诱导矩阵范数
,使得
,
,且
,
。根据以上范数,得到
.
假设当
,成立
.
则,当
时,有
因此,
,定理证毕。
4. 数值例子
考虑下面的空间分布阶时间分数阶方程:
,
边界值:
,
初始值:
.
且
,
,
其中
上述方程的精确解为
。
图1显示了这个例子的精确解和数值解的对比,可以看出,数值解与精确解非常吻合。表1显示了我们的数值方法在
时关于
的误差和收敛性。随着
的减少,
的收敛阶达到二阶。表2表示了在
时关于h的误差和收敛性,随着h的减少,h的收敛阶也达到二阶。表3表示了在
时
的收敛阶,可以看出当
减少时,
的收敛阶是
。从下面图表的误差和收敛阶可以看出,我们的数值方法是有效的,稳定的。
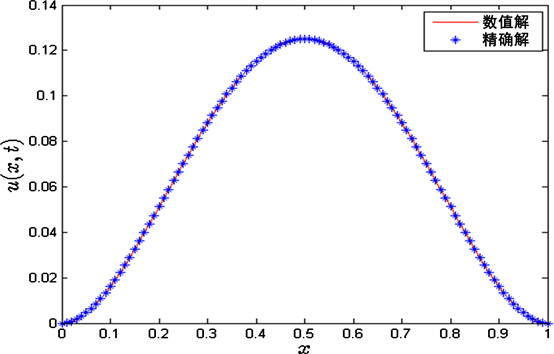
Figure 1. Exact solution and numerical solution with
at
and
图1. 在
时的数值解和精确解

Table 1. The error and the convergence order of σ for τ = h = 1 / 1000 at t = 1 and β = 0.7
表1. 在
时
的误差和收敛阶

Table 2. The error and the convergence order of h for τ = σ = 1 / 500 at and β = 0.7
表2. 在
时h的误差和收敛阶

Table 3. The error and the convergence order of τ for h = σ = 1 / 400 at t = 1 and β = 0.7
表3. 在
时
的误差和收敛阶
5. 结论
本文讨论了空间分布阶时间分数阶扩散方程的数值解。首先,基于有限体积法,得到了该方程的离散格式。其次,证明了离散格式的无条件稳定性和收敛性。最后,通过一个算例验证了该方法的有效性。在未来,我们希望能提出一种新的数值方法来求解二维的空间分布阶时间分数阶扩散方程,并提高其收敛速度。
基金项目
本研究由湖南省自然科学基金资助(批准号:No.2018JJ3519)和湖南省教育厅科研项目(批准号:NO.17B003)。
文章引用
杨莹莹,李 景. 空间分布阶时间分数阶扩散方程的有限体积法
Finite Volume Method for a Space Distributed-Order Time-Fractional Diffusion Equation[J]. 理论数学, 2019, 09(03): 351-361. https://doi.org/10.12677/PM.2019.93047
参考文献
- 1. Caputo, M. (1995) Mean Fractional-Order-Derivatives Differential Equations and Filters. Annali dell Universita di Ferrara, 41, 73-84.
- 2. Hu, X., Liu, F., Turner, I. and Anh, V. (2016) An Implicit Numerical Method of a New Time Distributed-Order and Two-Sided Space-Fractional Advection-Dispersion Equation. Numerical Algorithms, 72, 393-407.
https://doi.org/10.1007/s11075-015-0051-1
- 3. Bu, W., Xiao, A. and Zeng, W. (2017) Finite Difference/Finite Element Methods for Distributed-Order Time Fractional Diffusion Equations. Journal of Scientific Computing, 72, 422-441.
https://doi.org/10.1007/s10915-017-0360-8
- 4. Li, Z., Luchko, Y. and Yamamoto, M. (2017) Analyticity of Solutions to a Distributed Order Time-Fractional Diffusion Equation and Its Application to an Inverse Problem. Computers and Mathematics with Applications, 73, 1041-1052.
https://doi.org/10.1016/j.camwa.2016.06.030
- 5. Liu, Q., Mu, S., Liu, Q., Liu, B., Bi, X., Zhuang, P. and Li, B. (2018) An RBF Based Meshless Method for the Distributed Order Time Fractional Advection-Diffusion Equation. Engineering Analysis with Boundary Elements, 96, 55-63.
https://doi.org/10.1016/j.enganabound.2018.08.007
- 6. Li, J., Liu, F., Feng, L. and Turner, I. (2017) A Novel Finite Volume Method for the Riesz Space Distributed-Order Advection Diffusion Equation. Applied Mathematical Modelling, 46, 536-553.
https://doi.org/10.1016/j.apm.2017.01.065
- 7. Jia, J. and Wang, H. (2018) A Fast Finite Difference Method for Distribut-ed-Order Space-Fractional Partial Differential Equations on Convex Domains. Computers and Mathematics with Applications, 75, 2031-2043.
https://doi.org/10.1016/j.camwa.2017.09.003
- 8. Zhang, Y. and Meerschaert, M. (2008) Particle Tracking for Time Fractional Diffusion. Physical Review E, 78, 1-7.
- 9. Soklov, I.M., Chechkin, A.V. and Klafter, J. (2004) Distributed-Order Fractional Kinetics. Acta Physica Polonica B, 35, 1323-1341.
- 10. Lin, Y. and Xu, C. (2007) Finite Difference/Spectral Approximations for the Time-Fractional Diffusion Equation. Journal of Computational Physics, 225, 1533-1552.
https://doi.org/10.1016/j.jcp.2007.02.001
- 11. Li, J., Liu, F., Feng, L. and Turner, I. (2017) A Novel Finite Volume Method for the Riesz Space Distributed-Order Diffusion Equation. Computers and Mathematics with Applications, 74, 772-783.
https://doi.org/10.1016/j.camwa.2017.05.017
- 12. Shen, S., Liu, F., Anh, V. and Turner, I. (2006) Detailed Analysis of a Con-servative Difference Approximation for the Time Fractional Diffusion Equation. Journal of Computational and Applied Mathematics, 22, 1-19.
https://doi.org/10.1007/bf02832034
- 13. Feng, L.B., Zhuang, P., Liu, F. and Turner, I. (2015) Stability and Convergence of a New Finite Volume Method for a Two-Sided Space-Fractional Diffusion Equation. Applied Mathematics and Computation, 257, 52-65.
https://doi.org/10.1016/j.amc.2014.12.060
NOTES
*通讯作者。







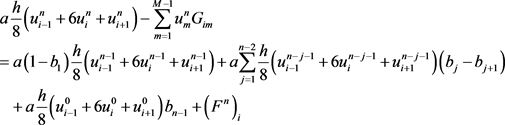 (11)
(11) 时,如果
或
,则D是严格对角占优的,且
时,如果
或
,则D是严格对角占优的,且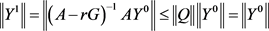 .
.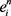 为点
处的误差。将
代入(10)和(11),并结合(7)和文献 [13] 的引理3,推论1,得到:
为点
处的误差。将
代入(10)和(11),并结合(7)和文献 [13] 的引理3,推论1,得到:
