Cayley子集S全为2阶元的点稳定子为F20的5度无核2-正则Cayley图 Core-Free Pentavalent 2-Regular Cayley Graphs Whose Cayley Subsets S Are All 2-Order Elements with Vertex Stabilizer F20

doi:10.12677/PM.2024.142058

Pure Mathematics
Vol. 14 No. 02 ( 2024 ), Article ID: 81722 , 7 pages
10.12677/PM.2024.142058

Cayley子集S全为2阶元的点稳定子为F₂₀的5度无核2-正则Cayley图

茹昕，凌波^*

●How to Cite this Article

云南民族大学数学与计算机科学学院，云南昆明

收稿日期：2024年1月19日；录用日期：2024年1月31日；发布日期：2024年2月29日

摘要

在具有较高对称性的图中，正则Cayley图是一类特殊的对称图。称一个图Γ为2-正则图，如果Γ的全自同构群AutΓ作用在2-弧集上正则。本文给出了点稳定子为F₂₀的5度无核2-正则Cayley图在Cayley子集全为2阶元情况下的全部分类。

关键词

无核，2-正则，Cayley图

Core-Free Pentavalent 2-Regular Cayley Graphs Whose Cayley Subsets S Are All 2-Order Elements with Vertex Stabilizer F₂₀

Xin Ru, Bo Ling^*

School of Mathematics and Computer Sciences, Yunnan Minzu University, Kunming Yunnan

Received: Jan. 19^th, 2024; accepted: Jan. 31^st, 2024; published: Feb. 29^th, 2024

ABSTRACT

Among graphs with higher symmetry, regular Cayley graphs are a special class of symmetric graphs. A graph Γ is called 2-regular if its full automorphism group AutΓ acts regularly on its 2-arcs. In this paper, it gives a complete classification of core-free pentavalent 2-regular Cayley graphs with the vertex stabilizer F₂₀, where all Cayley subsets are 2-order elements.

Keywords:Core-Free, 2-Regular, Cayley Graph

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

为方便研究，本文假设所有的图都是有限、简单、连通和无向的。

设Γ是一个图， $V Γ$ 、 $E Γ$ 、 $A r c Γ$ 和 $Aut Γ$ 分别代表图的顶点集、边集、弧集和全自同构群， $val Γ$ 表示图Γ的度数。

设 $X \leq Aut Γ$ ，s是一个正整数。一个图Γ被称为是 $(X, s)$ -弧传递的，如果X传递作用在Γ的 $s$ -弧集上，其中，s-弧是一个由 $s + 1$ 个顶点组成的 $(s + 1)$ -数组，且对于 $\forall i$ ， $v_{i - 1} \neq v_{i + 1}$ ，满足 $(v_{i - 1}, v_{i}) \in E Γ$ 。称图Γ为s-弧正则图，如果它的全自同构群在其弧集上是正则的。

设G是有限群，其单位元素是1，一个图Γ被称为G的一个Cayley图，如果在G中有一个子集S，满足 $1 \notin S$ ，且 $S = S^{- 1}$ ，使得

$V Γ = G$ ， $E Γ = {(s, s g) | g \in G, s \in S}$ ，

其中 $S^{- 1} = {s^{- 1} | s \in S}$ 。我们用 $Cay (G, S)$ 表示Cayley图Γ，Cayley图Γ的度数为 $| S |$ ，另外，G可以被看作 $Aut Γ$ 的一个正则子群，其中G右乘作用在 $V Γ$ 上。为了方便，我们仍然用G代表这个正则子群，则Cayley图是点传递的；相反，一个点传递图Γ是群G的一个Cayley图，当且仅当 $Aut Γ$ 包含同构于G的一个正则子群。一个Cayley图 $Cay (G, S)$ 被称为G的一个正规Cayley图，如果G是 $Aut (Cay (G, S))$ 的一个正规子群；称 $Cay (G, S)$ 是无核的，如果G在某些 $X \leq Aut (Cay (G, S))$ 中是无核的，即 ${Core}_{X} (G) : = \cap_{x \in X} G^{X} = 1$ 。

图的对称性研究一直都是群与图的一个热门话题，而Cayley图作为一种特殊的点传递图，因其构造简单、高度对称、品种多样，更是备受国内外学者的关注，有着丰富的研究成果，因此，正则Cayley图作为其中一类非常特殊的Cayley图，也得到了人们的广泛研究。对于一个图Γ，称图Γ为1-正则图，如果Γ的全自同构群 $Aut Γ$ 作用在其弧集上正则。图论学者最初从3度1-正则图开始研究，文献 [1] 中R. Frucht构造出了第一个3度1-正则图的例子；Li和Lou等在文献 [2] 中证明了如果5度的 $(X, 1)$ -正则Cayley图不是正规或双正规的，则它在同构意义下是两个无核图中其中一个的正规覆盖；Ling和Lou在文献 [3] 中给出了连通无核5度1-传递Cayley图的完全分类；Li和Lou在文献 [4] 中给出了7度无核1-正则Cayley图的完全分类；另外，关于5度图的更多性质和分类结果可参见文献 [5] [6] [7] [8] [9] 。

本文主要针对Cayley子集全为2阶元的点稳定子为F₂₀的5度无核2-正则Cayley图进行研究和分类，得到以下主要结果：

定理1.1 设 $Γ = Cay (G, S)$ 是无核5度2-正则Cayley图， ${(Aut Γ)}_{1}$ 是1在 $Aut Γ$ 中的稳定子，且同构于F₂₀，其中，Cayley子集全由2阶元组成，则下列之一成立：

1) Γ同构于表1中的一个图；

2) 存在一个 $Aut Γ$ 的子群X，使得 $G \leq X$ ，且G在X中无核。进一步，G和X的结构见表2。

Table 1. Core-Free pentavalent 2-regular Cayley graphs with vertex stabilizer F20

表1. 点稳定子为F₂₀的5度无核2-正则Cayley图

Table 2. Candidates for core-Free pentavalent 2-regular Cayley graphs with vertex stabilizer F20

表2. 点稳定子为F₂₀的5度无核2-正则Cayley图的候选

2. 预备知识

设X是有限群，H是X的无核子群，对于一个元素 $g \in X - H$ ，定义图 $Γ = Cos (X, H, g)$ ，顶点集 $[X : H]$ 是H在X中的右陪集，使得Hx和Hy相邻当且仅当 $y x^{- 1} \in H g H$ ，则 $X \leq Aut Γ$ 在它的弧集上传递，其中X右乘作用在 $[X : H]$ 上，这样的图叫做陪集图，且Γ连通当且仅当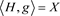，Γ的度为 $| H : H \cap H^{g} |$ 。另外，若有一个正则子群G，则 $Γ = Cay (G, G \cap H g H)$ 。

对于一个无核X-弧传递Cayley图 $Γ = Cay (G, S)$ ，其中 $G \leq X \leq Aut Γ$ ，设 $v \in V Γ$ ， $H = X_{v}$ 是v在X中的稳定子群，假设 $| H | = n$ ，考虑X在 $[X : G]$ 上的右乘作用，则X是对称群 $S_{n}$ 的一个子群，在这个作用下，H是 $S_{n}$ 的一个正则子群，且G是X中 $i \in {1, 2, \dots, n}$ 的一个稳定子，不失一般性，我们可以假设G稳定1。由(文献 [10] ，命题3.2)，我们有以下结论：

引理2.1 设 $Γ = Cay (G, S)$ 是一个无核X-弧传递Cayley图， $G \leq X \leq Aut Γ$ ，设 $v \in V Γ$ ， $H = X_{v}$ 是v在X中的稳定子群，假设 $| H | = n$ ，则X是 $S_{n}$ 的一个子群，且H正则作用在 ${1, 2, \dots, n}$ 上。另外，若S包含一个对合 $τ$ ，则 $τ \in N_{S_{n}} (H \cap H^{τ}) - (\cup_{1 \neq K ⊲ H} N_{S_{n}} (K))$ ， $Γ ≅ Cos (X, H, τ)$ ， $X = 〈 H, τ 〉$ ， $G = {σ \in X | 1^{σ} = 1}$ ， $S = {σ \in H τ H | 1^{σ} = 1}$ 。

对于连通5度 $(X, s)$ -传递图，由文献 [8] 和 [9] ，我们有以下引理：

引理2.2 设Γ是一个5度 $(X, s)$ -传递图， $X \leq Aut Γ$ ，且 $s \geq 1$ ，设 $v \in V Γ$ ，F₂₀表示20阶的Frobenius群，则：

1) 如果 $X_{v}$ 是可解的，则 $| X_{v} | | 80$ ，且 $s \leq 3$ ，其中， $(X_{v}, s)$ 在表3中；

2) 如果 $X_{v}$ 是不可解的，则 $| X_{v} | | 2^{9} \cdot 3^{2} \cdot 5$ ，且 $2 \leq s \leq 5$ ，其中， $(X_{v}, s)$ 在表4中。

Table 3. The soluble vertex stabilizer

表3. 可解的点稳定子

Table 4. The insoluble vertex stabilizer

表4. 不可解的点稳定子

3. 主要结论

设 $Γ = Cay (G, S)$ 是无核5度2-正则Cayley图，因我们仅考虑无向图，则 $S = S^{- 1}$ ，因此Cayley子集S中一定包含一个对合 $τ$ ，由引理2.1可知，H是S₂₀的一个正则子群。我们可以假设 $H = 〈 a, b 〉 ≅ F_{20}$ ，其中 $a = (113720) (215618) (3121016) (414919) (511817)$ ， $b = (115819) (212717) (314620)$ $(4111018) (513916)$ 。假设 $P = 〈 a 〉$ ，则 $Cay (G, S) ≅ Cos (X, H, τ)$ ，其中 $τ \in N_{S_{20}} (P) - (\cup_{1 \neq K ⊲ H} N_{S_{20}} (K))$ ， $X = 〈 H, τ 〉 \leq S_{20}$ ， $G = {σ \in X | 1^{σ} = 1}$ ， $S = {σ \in H τ H | 1^{σ} = 1}$ 。由Magma (文献 [11] )计算可得 $τ$ 有846种选择，它们在 $N_{S_{20}} (H)$ 中被分为159种共轭类。本文仅考虑Cayley子集S全为2阶元的情况，共有39种共轭类，它们的代表元如下：

$τ_{1} = (1117) (1216) (1320) (1419) (1518),$

$τ_{2} = (26) (310) (49) (58) (1117) (1216) (1419) (1518),$

$τ_{3} = (26) (310) (49) (58) (1320),$

$τ_{4} = (2 6) (15 18),$

$τ_{5} = (310) (49) (58) (1320) (1518),$

$τ_{6} = (312) (414) (511) (817) (919) (1016) (1320) (1518),$

$τ_{7} = (215) (4 9) (5 8) (618) (12 16) (1320),$

$τ_{8} = (2 18) (4 14) (5 11) (6 15) (8 17) (9 19) (12 16) (13 20),$

$τ_{9} = (2 18) (3 16) (6 15) (10 12) (11 17) (13 20) (14 19),$

$τ_{10} = (26) (4 19) (5 17) (8 11) (9 14) (12 16) (13 20),$

$τ_{11} = (2 15) (3 16) (419) (5 11) (6 18) (817) (9 14) (10 12) (13 20),$

$τ_{12} = (2 15) (3 12) (414) (5 11) (6 18) (817) (9 19) (10 16) (13 20),$

$τ_{13} = (2 18) (3 16) (419) (5 17) (6 15) (811) (9 14) (10 12) (13 20),$

$τ_{14} = (218) (615) (11 17) (12 16) (1320) (14 19),$

$τ_{15} = (215) (618) (11 17) (12 16) (1320) (14 19),$

$τ_{16} = (3 10) (4 9) (5 8) (11 17) (12 16) (1419),$

$τ_{17} = (2 6) (3 10) (12 16) (15 18),$

$τ_{18} = (3 16) (4 19) (5 17) (8 11) (9 14) (10 12) (13 20) (15 18),$

$τ_{19} = (4 14) (5 11) (8 17) (9 19) (12 16) (13 20) (15 18),$

$τ_{20} = (2 6) (4 14) (5 11) (8 17) (9 19) (12 16) (13 20),$

$τ_{21} = (2 15) (419) (5 17) (6 18) (811) (9 14) (12 16) (1320),$

$τ_{22} = (2 18) (3 12) (4 14) (5 11) (6 15) (817) (919) (10 16) (13 20),$

$τ_{23} = (2 15) (3 16) (4 19) (5 17) (6 18) (811) (914) (10 12) (13 20),$

$τ_{24} = (2 15) (3 10) (4 9) (5 8) (618) (13 20),$

$τ_{25} = (2 6) (3 16) (4 19) (5 17) (811) (9 14) (10 12) (13 20),$

$τ_{26} = (2 18) (3 10) (4 9) (5 8) (6 15) (13 20),$

$τ_{27} = (2 18) (3 16) (4 14) (5 11) (6 15) (8 17) (9 19) (10 12) (13 20),$

$τ_{28} = (3 16) (4 14) (5 11) (8 17) (9 19) (10 12) (13 20) (15 18),$

$τ_{29} = (2 6) (3 12) (4 19) (5 17) (8 11) (9 14) (10 16) (13 20),$

$τ_{30} = (2 6) (3 16) (4 14) (5 11) (8 17) (9 19) (10 12) (13 20),$

$τ_{31} = (3 12) (419) (5 17) (811) (9 14) (10 16) (1320) (15 18),$

$τ_{32} = (3 12) (4 9) (58) (10 16) (13 20) (15 18),$

$τ_{33} = (215) (3 10) (4 19) (5 17) (618) (811) (914) (13 20),$

$τ_{34} = (215) (3 12) (4 9) (5 8) (618) (10 16) (1320),$

$τ_{35} = (26) (3 10) (419) (517) (811) (914) (1320),$

$τ_{36} = (215) (3 16) (618) (10 12) (1117) (1320) (1419),$

$τ_{37} = (218) (3 12) (49) (58) (615) (10 16) (1320),$

$τ_{38} = (2 15) (3 16) (49) (58) (6 18) (10 12) (13 20),$

$τ_{39} = (2 18) (3 12) (58) (6 15) (10 16) (13 20) (1419) .$

现在设 $Ω = {1, 2, \dots, 20}$ ， $X_{j} = 〈 H, τ_{j} 〉$ ， $Γ_{j} = Cos (X_{j}, H, τ_{j})$ ，其中 $j = 1, 2, \dots, 39$ 。设 $G_{j} = {σ \in X_{j} | 1^{σ} = 1}$ ， $S_{j} = {σ \in H τ_{j} H | 1^{σ} = 1}$ 。注意到，H是 $X_{j}$ 的一个正则子群， $G_{j}$ 是 $X_{j}$ 作用在 $Ω$ 上的1的点稳定子。由此， $X_{j} = G_{j} H$ ，且 $G_{j} \cap H = 1$ ，则 $G_{j}$ 正则作用在 $[X_{j} : H]$ 上，进而得 $Γ_{j} = Cay (G_{j}, S_{j})$ 。本文主要结论如下：

引理3.1对于 $j = 1, 2, \dots, 11$ ，如果 $Γ_{j}$ 是2-正则图，则：

1) $j = 5$ ， $G_{5} ≅ ℤ_{2}^{8} : S_{4}$ ， $Aut Γ_{5} ≅ ℤ_{2}^{8} : (ℤ_{2}^{2} : S_{5})$ ， $S_{5} = {τ_{5}, a_{5}, b_{5}, c_{5}, d_{5}}$ ，且 $Γ_{5} ≅ Cay (G_{5}, S_{5})$ ；

2) $j = 7, 11$ ， $G_{7} ≅ G_{11} ≅ ℤ_{2}^{5} : (Q_{8} : S_{4})$ ， $Aut Γ_{7} ≅ Aut Γ_{11} ≅ ℤ_{2}^{8} : (ℤ_{2}^{2} : S_{5})$ ， $S_{7} = {τ_{7}, a_{7}, b_{7}, c_{7}, d_{7}}$ ， $S_{11} = {τ_{11}, a_{11}, b_{11}, c_{11}, d_{11}}$ ，且 $Γ_{7} ≅ Cay (G_{7}, S_{7})$ ， $Γ_{11} ≅ Cay (G_{11}, S_{11})$ 。

证明：首先，我们可由Magma分别计算出 $Aut Γ_{j}$ 和 $G_{j}$ 的阶和正规子群以及 $S_{j}$ 中的元素。

对于一个顶点 $v \in V Γ_{j}$ ， $| {(Aut Γ_{1})}_{v} | = 2880$ ， $| {(Aut Γ_{2})}_{v} | = | {(Aut Γ_{4})}_{v} | = | {(Aut Γ_{6})}_{v} | = | {(Aut Γ_{8})}_{v} | = | {(Aut Γ_{9})}_{v} |$ $= | {(Aut Γ_{10})}_{v} | = 120$ ，则由引理2.2，这些图都不是2-传递图，进而也不是2-正则图。另外， $| {(Aut Γ_{3})}_{v} | = 40$ ， $| {(Aut Γ_{5})}_{v} | = | {(Aut Γ_{7})}_{v} | = | {(Aut Γ_{11})}_{v} | = 20$ ，因此， $Γ_{3}$ 也不是2-正则图， $Γ_{5}$ 、 $Γ_{7}$ 、 $Γ_{11}$ 是2-正则图。下面分别对这三个2-正则图的结构进行分析：

当 $j = 5$ 时，G₅有一个256阶的正规子群是初等交换群 $ℤ_{2}^{8}$ ，且它的补与S₄同构； $Aut Γ_{5}$ 存在一个正规子群是初等交换群 $ℤ_{2}^{8}$ ，它的补的阶为480，将这个补群记为 $C A_{5}$ ，则 $C A_{5}$ 中有一个正规子群是初等交换群 $ℤ_{2}^{2}$ ，且它的补与S₅同构。所以，我们得 $G_{5} ≅ ℤ_{2}^{8} : S_{4}$ ， $Aut Γ_{5} ≅ ℤ_{2}^{8} : (ℤ_{2}^{2} : S_{5})$ 。

当 $j = 7, 11$ 时， $| G_{7} | = | G_{11} | = 2^{11} \cdot 3$ ，G₇和G₁₁均有29个正规子群，且其中一个正规子群是初等交换群 $ℤ_{2}^{5}$ ，记 $ℤ_{2}^{5}$ 在G₇和G₁₁中的补群分别为C₇和C₁₁，则C₇和C₁₁中均有一个正规子群与四元数群Q₈同构，且C₇和C₁₁在G₇和C₁₁中的补群同构于S₄，从而得 $G_{7} ≅ G_{11} ≅ ℤ_{2}^{5} : (Q_{8} : S_{4})$ ；另外， $Aut Γ_{7}$ 和 $Aut Γ_{11}$ 的正规子群中均有一个是初等交换群 $ℤ_{2}^{8}$ ， $ℤ_{2}^{8}$ 在 $Aut Γ_{7}$ 和 $Aut Γ_{11}$ 中的补群分别记为 $C A_{7}$ 和 $C A_{11}$ ，则 $C A_{7}$ 和 $C A_{11}$ 中均有一个正规子群同构于 $ℤ_{2}^{2}$ ，且 $ℤ_{2}^{2}$ 在 $C A_{7}$ 和 $C A_{11}$ 中的补群同构于S₅，从而得 $Aut Γ_{7} ≅ Aut Γ_{11} ≅ ℤ_{2}^{8} : (ℤ_{2}^{2} : S_{5})$ ，引理得证。

引理3.2 对于 $j = 12, 13, 14, 15$ ， $G_{12} ≅ G_{13} ≅ G_{14} ≅ G_{15} ≅ ℤ_{2}^{9} : S_{9}$ ， $X_{12} ≅ X_{13} ≅ X_{14} ≅ X_{15} ≅ ℤ_{2}^{10} : S_{10}$ ，且 $S_{j} = {τ_{j}, a_{j}, b_{j}, c_{j}, d_{j}}$ ， $Γ_{j} ≅ Cay (G_{j}, S_{j})$ 。

证明：首先由Magma可直接计算出Cayley子集 $S_{j}$ 中的元素以及 $G_{j}$ 的阶和正规子群。

当 $j = 12, 13, 14, 15$ 时， $G_{j}$ 的阶 $| G_{j} | = 2^{16} \cdot 3^{4} \cdot 5 \cdot 7$ ，初等交换群 $ℤ_{2}^{9}$ 是它们中的一个正规子群，且 $ℤ_{2}^{9}$ 在 $G_{j}$ 中的补群与S₉同构，进而可得 $G_{j} ≅ ℤ_{2}^{9} : S_{9}$ ；另外，因陪集图连通当且仅当 $X = 〈 τ, H 〉$ ，又 $H = 〈 a, b 〉$ ，则有 $X_{j} = 〈 a, b, τ_{j} 〉$ ，由此我们可以得到 $X_{j}$ 有9个正规子群，其中一个正规子群是初等交换群 $ℤ_{2}^{10}$ ，且 $ℤ_{2}^{10}$ 在 $X_{j}$ 中的补群同构于S₁₀，最终有 $X_{j} ≅ ℤ_{2}^{10} : S_{10}$ ，引理得证。

引理3.3 对于 $j = 16, 17$ ， $G_{16} ≅ G_{17} ≅ ℤ_{2}^{8} : (A_{5} : S_{4})$ ， $X_{16} ≅ X_{17} ≅ ℤ_{2}^{8} : ((A_{5} \times A_{5}) : (ℤ_{2} \times ℤ_{4}))$ ，且 $S_{j} = {τ_{j}, a_{j}, b_{j}, c_{j}, d_{j}}$ ， $Γ_{j} ≅ Cay (G_{j}, S_{j})$ 。

证明：假设 $j = 16, 17$ ，由Magma可计算出Cayley子集S₁₆和S₁₇中的元素，且 $| G_{16} | = | G_{17} | = 2^{13} \cdot 3^{2} \cdot 5$ ， $| X_{16} | = | X_{17} | = 2^{15} \cdot 3^{2} \cdot 5^{2}$ ，G₁₆和G₁₇中均有一个阶为256的正规子群是初等交换群 $ℤ_{2}^{8}$ ，它在G₁₆和G₁₇中的补群分别记为C₁₆和C₁₇，则C₁₆和C₁₇中的一个正规子群同构于A₅，且C₁₆和C₁₇分别在G₁₆和G₁₇中的补群与S₄同构，从而得 $G_{16} ≅ G_{17} ≅ ℤ_{2}^{8} : (A_{5} : S_{4})$ 。

进一步地，因 $X_{16} = 〈 a, b, τ_{16} 〉$ ， $X_{17} = 〈 a, b, τ_{17} 〉$ ，我们可得X₁₆和X₁₇的阶，它们中均有一个阶为256的正规子群是初等交换群 $ℤ_{2}^{8}$ ，记 $ℤ_{2}^{8}$ 在X₁₆和X₁₇中的补群分别记为CX₁₆和CX₁₇，且CX₁₆和CX₁₇中的一个阶为3600的正规子群只有两个阶为60且交为1的非平凡正规子群，因此这个正规子群同构于两个A₅的直积，且这个正规子群在CX₁₆和CX₁₇中的补群是交换群但并非初等交换群，且不同构于循环群 $ℤ_{8}$ ，所以该补群必与 $ℤ_{2} \times ℤ_{4}$ 同构，从而得 $X_{16} ≅ X_{17} ≅ ℤ_{2}^{8} : ((A_{5} \times A_{5}) : (ℤ_{2} \times ℤ_{4}))$ ，引理得证。

引理3.4 对于 $j = 18, 19, 20, 21$ ， $G_{j} ≅ ℤ_{2}^{8} : S_{9}$ ， $X_{j} ≅ (ℤ_{2}^{9} : A_{10}) : ℤ_{2}$ ，且 $S_{j} = {τ_{j}, a_{j}, b_{j}, c_{j}, d_{j}}$ ， $Γ_{j} ≅ Cay (G_{j}, S_{j})$ 。

证明：首先，我们可以由Magma直接计算出Cayley子集 $S_{j}$ 中的元素以及 $G_{j}$ 和 $X_{j}$ 的阶和正规子群。

当 $j = 18, 19, 20, 21$ 时， $G_{j}$ 有4个正规子群，其中一个正规子群是初等交换群 $ℤ_{2}^{8}$ ，且 $ℤ_{2}^{8}$ 在 $G_{j}$ 中的补群与置换群S₉同构，因此 $G_{j} ≅ ℤ_{2}^{8} : S_{9}$ 。另一方面， $X_{j}$ 有5个正规子群，它的阶为 $| X_{j} | = 2^{17} \cdot 3^{4} \cdot 5^{2} \cdot 7$ ，将 $X_{j}$ 中一个阶为 $2^{16} \cdot 3^{4} \cdot 5^{2} \cdot 7$ 的正规子群记为 $N_{j}$ ，则 $N_{j}$ 中的一个正规子群是初等交换群 $ℤ_{2}^{9}$ ，且 $ℤ_{2}^{9}$ 在 $N_{j}$ 中的补群与A₁₀同构，进而得 $N_{j} ≅ ℤ_{2}^{9} : A_{10}$ ，且 $N_{j}$ 在 $X_{j}$ 中的补群是2阶循环群，因此 $X_{j} ≅ (ℤ_{2}^{9} : A_{10}) : ℤ_{2}$ ，引理得证。

引理3.5 对于 $j = 22, 23, \dots, 39$ ， $G_{j} ≅ A_{19} : ℤ_{2}$ ， $X_{j} ≅ A_{20} : ℤ_{2}$ ，且 $S_{j} = {τ_{j}, a_{j}, b_{j}, c_{j}, d_{j}}$ ， $Γ_{j} ≅ Cay (G_{j}, S_{j})$ 。

证明：首先，我们可以由Magma直接计算出 $G_{j}$ 和 $X_{j}$ 的阶 $| G_{j} | = 2^{16} \cdot 3^{8} \cdot 5^{3} \cdot 7^{2} \cdot 11 \cdot 13 \cdot 17 \cdot 19$ ， $| X_{j} | = 2^{18} \cdot 3^{8} \cdot 5^{4} \cdot 7^{2} \cdot 11 \cdot 13 \cdot 17 \cdot 19$ ，以及它们的3个正规子群。

当 $j = 22, 23, \dots, 39$ 时， $G_{j}$ 有一个阶为 $2^{15} \cdot 3^{8} \cdot 5^{3} \cdot 7^{2} \cdot 11 \cdot 13 \cdot 17 \cdot 19$ 的非平凡正规子群，将其记为 $N G_{j}$ ，则 $N G_{j}$ 只有2个正规子群，即单位元1和它本身，因此 $N G_{j}$ 是单群，同构于交错群A₁₉，且 $N G_{j}$ 在 $G_{j}$ 中的补群与2阶循环群 $ℤ_{2}$ 同构，因此 $G_{j} ≅ A_{19} : ℤ_{2}$ ；同样地，我们将 $X_{j}$ 的非平凡正规子群记为 $N X_{j}$ ，则 $N X_{j}$ 也是单群，与交错群A₂₀同构，且 $N X_{j}$ 在 $X_{j}$ 中的补群同构于二阶循环群 $ℤ_{2}$ ，进而得 $X_{j} ≅ A_{20} : ℤ_{2}$ ，引理得证。

对于点稳定子为F₂₀的5度无核2-正则Cayley图Γ，其Cayley子集S中包含的对合 $τ$ 在 $N_{S_{20}} (H)$ 中共有159种共轭类，本文仅讨论Cayley子集S全为2阶元的情况，共轭类共有39种，其 $Aut Γ$ 、X和G的结构描述在定理1.1中的表格中，在本文的研究基础上，我们之后可以继续研究Cayley子集不全为2阶元的情况，进而可以得到点稳定子为F₂₀的5度无核2-正则Cayley图的完全分类。通过研究和分析，本文证明了在同构意义下，Cayley子集S全为2阶元的点稳定子为F₂₀的5度无核2-正则Cayley图至多只有31个，综合引理3.1、引理3.2、引理3.3、引理3.4和引理3.5的证明，定理1.1得证。

文章引用

茹昕,凌波. Cayley子集S全为2阶元的点稳定子为F₂₀的5度无核2-正则Cayley图
Core-Free Pentavalent 2-Regular Cayley Graphs Whose Cayley Subsets S Are All 2-Order Elements with Vertex Stabilizer F₂₀[J]. 理论数学, 2024, 14(02): 599-605. https://doi.org/10.12677/PM.2024.142058

参考文献

1. Frucht, R. (1952) A One-Regular Graph of Degree Three. Canadian Journal of Mathematics, 4, 240-247. https://doi.org/10.4153/CJM-1952-022-9

2. Li, J.J., Lou, B.G. and Zhang, X.J. (2013) Finite 1-Regular Cayley Graphs of Valency 5. International Journal of Combinatorics, 2013, Article ID: 125916. https://doi.org/10.1155/2013/125916

3. Ling, B., Lou, B.G. and Li, J.J. (2016) On Pentavalent 1-Transitive Cayley Graphs. Discrete Mathematics, 339, 1335-1343. https://doi.org/10.1016/j.disc.2015.11.018

4. Li, J.J., Zhang, G.R. and Ling, B. (2013) 1-Regular Cayley Graphs of Valency 7. Bulletin of the Australian Mathematical Society, 88, 479-485. https://doi.org/10.1017/S0004972713000087

5. Guo, S.T., Feng, Y.Q. and Li, C.H. (2013) The Finite Edge-Primitive Pentavalent Graphs. Journal of Algebraic Combinatorics, 38, 491-497. https://doi.org/10.1007/s10801-012-0412-y

6. Hua, X.H., Feng, Y.Q. and Lee, J. (2011) Pentavalent Symmetric Graphs of Order 2pq. Discrete Mathematics, 311, 2259-2267. https://doi.org/10.1016/j.disc.2011.07.007

7. Li, Y.T. and Feng, Y.Q. (2010) Pentavalent One-Regular Graphs of Square-Free Order. Algebra Colloquium, 17, 515-524. https://doi.org/10.1142/S1005386710000490

8. Zhou, J.X. and Feng, Y.Q. (2010) On Symmetric Graphs of Valency Five. Discrete Mathematics, 310, 1725-1732. https://doi.org/10.1016/j.disc.2009.11.019

9. Guo, S.T. and Feng, Y.Q. (2012) A Note on Pentavalent s-Transitive Graphs. Discrete Mathematics, 312, 2214-2216. https://doi.org/10.1016/j.disc.2012.04.015

10. Li, J.J. and Lu, Z.P. (2009) Cubic s-Arc Transitive Cayley Graphs. Discrete Mathematics, 309, 6014-6025. https://doi.org/10.1016/j.disc.2009.05.002

11. Bosma, W., Cannon, C. and Playoust, C. (1997) The Magma Al-gebra System I: The User Language. Journal of Symbolic Computation, 24, 235-265. https://doi.org/10.1006/jsco.1996.0125

期刊菜单