Computer Science and Application
Vol.
10
No.
11
(
2020
), Article ID:
38833
,
12
pages
10.12677/CSA.2020.1011219
基于季节性ARIMA模型的新零售精准预测
唐玮煜*#,黄鸿亮*#,杨俊涛
吉林大学珠海学院,广东 珠海

收稿日期:2020年11月4日;录用日期:2020年11月19日;发布日期:2020年11月26日

摘要
本文旨在建立新零售的精准预测模型,首先通过对新零售目标商品的主要指标数据进行数据预处理,接着建立Pearson相关系数模型,使用Python分析得到热力图,确定销售量具有较好的预测性并存在自相关性,将其作为本文预测模型的重要决策变量,然后建立差分整合移动平均自回归模型(Autoregressive Integrated Moving Average model,简称ARIMA),同时考虑商品由于季节所造成的影响,并优化成季节性ARIMA预测模型,最后使用平均绝对百分比误差(MAPE)评估模型,得到预测误差百分比均值为19.33%。本文模型预测误差小,对新零售商品的预测具有指导意义。
关键词
精准预测,时间序列分析,季节性ARIMA模型,平均绝对百分比误差
Accurate Forecast of New Retail Based on Seasonal ARIMA Model
Weiyu Tang*#, Hongliang Huang*#, Juntao Yang
Zhuhai College of Jilin University, Zhuhai Guangdong

Received: Nov. 4th, 2020; accepted: Nov. 19th, 2020; published: Nov. 26th, 2020

ABSTRACT
The purpose of this paper is to establish an accurate prediction model of new retail. Firstly, the main index data of new retail target goods are preprocessed, and then Pearson correlation coefficient model is established. The thermodynamic diagram is obtained by Python analysis. The sales volume is confirmed to have good predictability and existing autocorrelation. Then the Autoregressive Integrated Moving Average model (ARIMA) is established. At the same time, the seasonal ARIMA prediction model is optimized considering the same influence of the season. Finally, the average absolute percentage error (MAPE) evaluation model is used to obtain the average forecast error percentage of 19.33%. The prediction error of the model in this paper is small, which has guiding significance for the prediction of commodities.
Keywords:Accurate Prediction, Time Series Analysis, Seasonal ARIMA Model, MAPE

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在市场发展日新月异的背景下,市场上诞生出了新零售的模式,新零售将电商与线下结合在一起,运用大数据、云计算、人工智能、物流系统等新技术,大大地提升了服务质量,同时又解决了传统零售模式下消费者购物体验痛点 [1]。而在这种模型下,顾客的需求不仅仅局限于追求实用性,更考虑了时尚性、个性化、用户体验等等特殊需求。基于这些需求,新零售企业的生产模式逐渐变得复杂且凌乱,既要满足“量”上的需求,又要迎合“质”、“感”、“美”的追求,这给零售行业的库存管理带来了极大的挑战。如何根据层级复杂,品类繁多的历史销售数据,以区域层级,小类层级乃至门店skc (单款单色)层级给出精准的需求预测,是当前大多数新零售企业需要重点关注并思考的问题。
在众多的预测方法中,时间序列预测模型以连续性原理作为依据,适用于对新零售商品销量的预测。以Box-Jenkins (ARIMA)方法为代表的现代时间序列预测方法以随机过程理论为理论基础,其结构简单,建模速度快,且预测误差小 [2]。因此,本文基于中国优选法统筹法与经济数学研究会举办的竞赛提供的数据,根据Box-Jenkins方法建立季节性ARIMA模型,对新零售目标商品的主要指标数据进行数据处理及分析,并建立相应模型,为解决新零售行业的精准需求预测提供较有意义的思路。
2. 基于ARIMA的拟合模型
2.1. 数据预处理
本文研究简要流程图,如图1所示。
首先对4个附件进行分析,得到各个表的具体含义分别为:sale_info产品流水数据、prod_info产品具体信息、inv_info库存信息、holiday_info节假日具体日期。
通过研究分析,确定目标skc为销售时间处于2018年7月1日至 2018年10月1日内且累计销售额排名前50的skc,以下称为“目标skc”。
本文研究国庆、双十一、双十二和元旦四个节假日的各因素对目标skc的影响。下面利用Excel对附件进行升序、筛选、分类汇总和Vlookup函数计算。通过对sale_info表筛选(使用Excel筛选与升序)得到2018年7月1日至10月1日的流水数据,可以得到该时间段的skc、销售量和real_cost (实际出费)。利用Excel计算real_cost,得到real_cost数值排名为前五十的skc,即为目标skc。

Figure 1. Research brief flow chart
图1. 研究简要流程图
目标skc累积销售额如图2所示。

Figure 2. Target skc cumulative sales
图2. 目标skc累积销售额
接下来,对节假日的目标skc销售量的影响因素进行研究。根据对表格数据进行分析,选择产品销售量、产品总销售额、产品销售单价、最后一天库存数量、折扣、标签价格六个相关因素作为研究指标,在定性与定量的角度进行数学建模,研究这六个因素对目标skc的影响程度。
通过数据处理发现部分节假日时间靠后或是在年末时间的库存是搜索不到的,抽取2018年某一个skc的库存变化率,利用Excel可视化,得到图3。可以发现库存量是总体递减的,而四个节假日的产品优惠导致库存量快速下降或是断货,所以把节假日库存数量的缺失值定为0。

Figure 3. Inventory change chart of a certain skc in one year
图3. 某一个skc一年的库存变化图
通过数据预处理后,得到了国庆、双十一、双十二和元旦的在目标skc时期的销售量、销售单价、总的销售额、折扣、库存和标价数据,同时也有目标skc的销售量数据,下面分别使用四个节假日的相关因素对目标skc的销售量进行Python相关性分析。
利用Python进行Pearson相关性分析,其含义如下:如果想要验证两个变量或是多个变量之间的相关程度,通过计算相关性可以得到各个变量之间相关系数和相关系数矩阵,相关系数处于[0, 1],当变量之间的相关系数越接近1,变量间的相关程度就越大,当相关系数为0,称两者不存在线性相关关系。
为了评价并且量化四个节日的六个要素对问题中的目标skc的销售量的关联程度,所以建立Pearson相关系数模型。
若 与 的协方差 存在(且 ),称 为X的相关矩阵,其计算公式如下 [3]:
(1)
其中
(2)
是随机变量 的方差,而 为 的标准差。
利用Python进行相关系数模型的求解 [4] 并对六个相关矩阵进行可视化,得到热力图 如图4所示。从而得到销售量、销售单价、总的销售额、折扣、库存和标价数据与目标skc销售量的相关程度。
对Pearson相关系数矩阵中的各个因素进行相关分析的显著性检验 (significance test)。
1. 显著性检验就是事先对总体(随机变量)的参数或总体分布形式做出一个假设,然后利用样本信息来判断这个假设(备择假设)是否合理,即判断总体的真实情况与原假设是否有显著性差异;
2. 显著性检验是针对总体所做的假设做检验,原理是“小概率事件实际不可能性原理”来接受或否定假设;
3. 显著性检验用于实验处理组与对照组或两种不同处理的效应之间是否有差异,以及这种差异是否显著的方法。
使用SPSS软件进行对相关性的显著性分析(显著性水平 为0.05),得到显著性检验表,见表1:
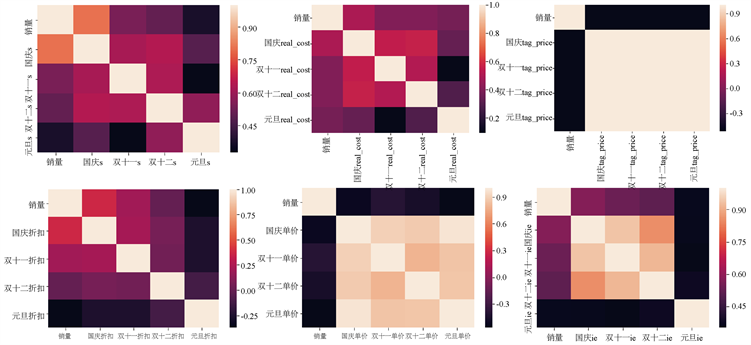
Figure 4. Correlation matrix thermodynamic diagram
图4. 相关矩阵热力图
Table 1. Significance test table
表1. 显著性检验表
大部分相关因素的显著性 ,可以得到Pearson相关系数模型的效果较好。
根据热力图与显著性检验,可以看到与目标skc销售量相关系数较大的是节假日销售量、库存和标签价,说明这三个因素影响较大并且显著相关;而总销售额、销售单价和折扣的影响较小,相关系数较低。对于节假日销售量来说,相关性最高的是目标skc销售量与国庆的销售量,而其余三个节假日随着时间间隔越大,相关性越小,所以可以判断距离时间越远,相关程度越小。可视化图像反映出目标skc与销售量的相关程度较高,节假日销售量对目标skc的影响程度大,初步判断销售量之间有一定程度的自相关性和预测性,所以将销售量作为本文研究的主要决策变量,建立时间序列模型。
2.2. ARIMA模型的建立
本文需要对新零售目标产品的需求进行预测,通过2019年6月1日~10月1日的目标小类销售量预测2019年10月、11月和12月的目标小类销售量。
小类即多种skc聚合在一起为一个类别。通过数据预处理,得到2019年6月1日~10月1日小类累计销售量排名前10的小类编号,称为目标小类编号(tiny_class_code),如图5所示。

Figure 5. Cumulative sales of top 10 target categories
图5. 前十名目标小类累计销售额
统计分析得到每一天的小类销售量,保证销售量数据充足,并得到该时间段的目标小类每一天的销售量。接下来,使用目标小类的销售量的时间序列,建立目标小类的时间序列模型 [5],称为销量时间序列模型(Time series model of sales volume,记为SV-ARIMA模型)。
时间序列模型(ARIMA模型)的建模步骤 是:
1. 首先对观察值序列进行平稳性检验;
2. 如果通过进行平稳性检验,如果没有通过,对序列进行差分运算,直到平稳性检验通过;
3. 如果平稳性检验通过,那么分析结束,进行白噪声检验;
4. 如果白噪声检验没有通过进行拟合ARMA模型,直到白噪声检验通过,通过后分析结束。
总体过程如图6所示。
使用目标小类(10个小类)编号的日期为2019年6月1日至10月1日的销售量进行时间序列模型分析 [6]。
Step1:首先使用Python对目标小类中的10个小类进行绘制在2019年6月1日至10月1日的销售量时序图,如图7所示。可以看出,目标小类销售量的时间序列不完全平稳,因此需要进行差分平稳化。
Step2:建立自相关函数ACF (autocorrelation function)计算公式 。
自相关函数ACF描述的是时间序列观测值与其过去的观测值之间的线性相关性。计算公式如下:
(3)
其中k表示滞后期数, 表示序列值。使用Python得到10个小类的自相关图 [6],如图8所示。
Step3:根据自相关图可见,为了对通过平稳性检验,需要对序列进行差分运算,那么可以得到时间序列的d阶差分为:
(4)
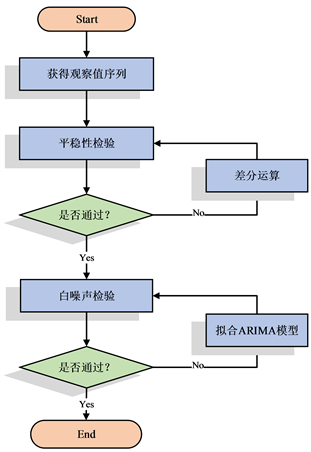
Figure 6. ARIMA modeling flow chart
图6. ARIMA建模流程图
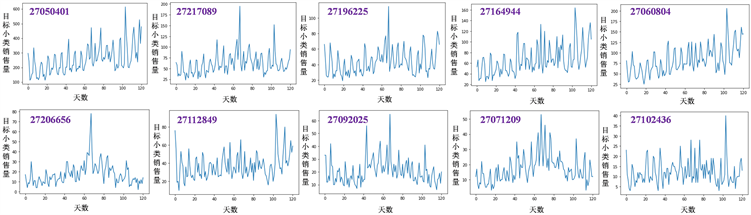
Figure 7. The time series chart of small sales target
图7. 目标小类的销售量时序图
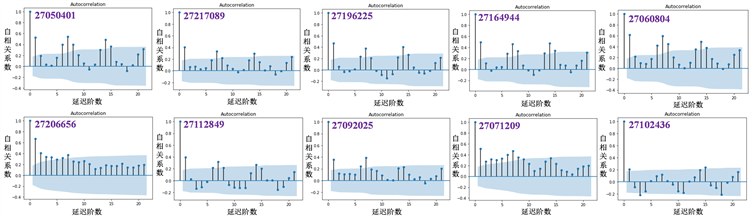
Figure 8. Autocorrelation graph of target subclass
图8. 目标小类的自相关图
可改写成:
(5)
其中, 为目标小类中一个小类的销售量时间序列。此式子为 关于 ( )的一个d阶自回归过程,其中 度量了自回归过程中产生的随机误差的大小是多少。差分运算通过自回归的方式提取了序列的确定性的信息。在本文需通过一阶差分和二阶差分运算的平稳性检验和后面一阶差分进行预测:
(6)
(7)
使用一阶差分对序列进行运算,并绘制出差分后序列之间的自相关图 [7],得到如图9所示的图像。
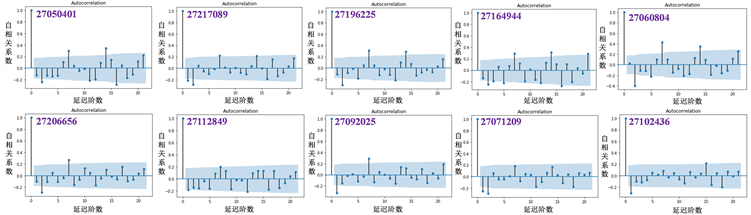
Figure 9. Autocorrelation graph after difference operation
图9. 差分运算后的自相关图
同时引入偏自相关函数概念:偏自相关函数PACF描述的是在给定中间观测值的条件下,时间序列观测值预期过去的观测值之间的线性相关性。使用Python绘制偏相关图 [7],得到图10。

Figure 10. Partial correlation graph after difference operation
图10. 差分运算后的偏相关图
Step4:接下来建立、拟合销量时间序列模型(SV-ARIMA模型),引入ARIMA模型的概念并建立模型 [6]。
若序列 可以通过d阶差分转化为平稳的时间序列后,即 是一个平稳时间序列,并且序列可以拟合成一个平稳可逆的 模型,则意味着序列 可以拟合成如下形式的数学模型:
(8)
其中,序列 为一个白噪声序列, 为延迟算子。并且有:
(9)
Step4的模型称为求和自回归移动平均模型。记作 。自回归移动平均模型(ARIMA)的目标是描述数据中彼此之间的关系。
其中,d为差分的阶数,p为差分序列拟合的ARMA模型的自回归阶数,q指的是差分序列拟合的ARMA模型d的移动平均的阶数,在本问取 ,,,得到:
(10)
使用Python的ARIMA库进行对目标小类中的10个小类进行拟合和自回归移动平均模型,得到效果如图11 所示:

Figure 11. Arima fitting curve of sales volume of target sub category
图11. 目标小类销售量ARIMA拟合曲线
其中,蓝色曲线为差分后的销售量时间序列,时间为2019年6月1日至10月1日,红色曲线为 拟合曲线(SV-ARIMA模型),可见拟合效果较优。接下来对2019年10月、11月和12月的目标小类销售量进行预测 [8]。
3. 季节性ARIMA的预测模型
通过建立了销售量的时间序列模型,即SV-ARIMA模型,可以发现小类的销售量在2019年6月1日至10月1日有部分时间点有突变,目标小类的销售量变化也是如此,通过对目标小类销售量的分析,判断这段时间的销售量一定程度上是因为节假日人们的购物欲望较强和季节性突变。
ARIMA的一个优化版就是季节性ARIMA [9] (即SARIMAX模型 )。用于建模和预测时间序列未来点的Python中的一种方法被称为SARIMAX,其代表具有eXogenous回归的季节性自动反馈集成移动平均值。
SARIMAX模型 把数据集和序列的季节性考虑进去,每个小类一共有122天的销售量数据,把销售量为0的天数进行剔除处理,并且每一个小类选择75%的数据为训练集,25%的数据为测试集。使用Python对SV-ARIMA模型进行优化建模,建立目标小类销售量的季节性 预测模型(即Sales Volume-Season-SARIMAX预测模型,所以简记作SV-SARIMAX预测模型)。
得到目标小类中的10个小类预测2019年10月1日后三个月每一天的销售量的预测值,并使用Python进行可视化,如图12所示。

Figure 12. Sarimax forecast curve of sales volume of target sub category
图12. 目标小类销售量SARIMAX预测曲线
通过季节性ARIMA模型得到10月、11月和12月的预测销售量,如表2所示。
Table 2. Sales volume reality and forecast results of target sub category
表2. 目标小类销售量真实及预测结果
4. 预测模型的检验
由于得到了预测数据,结合真实数据,对预测模型进行检验。引入平均绝对百分比误差(Mean Absolute Percentage Error)的计算公式:
(11)
其中, 表示真实值, 表示预测值,APE为百分比误差,n为指标集个数,i表示目标小类。范围 ,MAPE为0%表示完美模型,MAPE大于100%则表示劣质模型。
根据MAPE的计算公式,得到目标小类预测效果检验表,如表3所示:
总体来看,MAPE维持在一定范围上,三个月的MAPE指标平均值为19.33%,预测模型合理可靠。
Table 3. Test table for prediction effect of target subclass
表3. 目标小类预测效果检验表
5. 结束语
为了探讨国庆节、双十一、双十二与元旦这个节假日的各种相关因素对销售时间处于2018年7月1日至2018年10月1日内累计销售额排名前50的skc (即目标skc)销售量的影响,选取了四个节假日的销售量、总销售量、销售单价、库存、折扣和标签价格的数据,建立Pearson相关系数模型,计算6个因素与skc销量的皮尔逊相关系数来进行分析,得到节假日的这6个相关因素对目标skc的影响程度。得到结论:节假日销售量、库存和标签价格这3个因素对目标skc的相关性强,影响较大。所以说,保证销售量与库存的统一和产品的定价是比较重要的。
时间序列模型是常用的定量预测模型,可以预测发展趋势。根据层级复杂,品类繁多的历史销售数据,以小类层级和门店skc (单款单色)层级给出精准的需求预测,是当前大多数新零售企业需要重点关注并思考的问题。由于通过相关系数模型得到销售量的相关性是比较强的,所以依据产品销售量进行建立时间序列模型。根据销售数据、销售量出现概率,对新零售目标产品的精准需求建立优化的SARIMAX模型,也称季节性时间序列模型。
通过拟合季节性时间序列模型进行预测,考虑了季节的影响。对两个不同的层级进行预测。拟合季节性时间序列模型,得到历史销售时间处于2019年6月1日至2019年10月1日内且累计销售额排名的前10小类(即目标小类)的销售量的预测值。研究结果的方法具有合理性和一定程度的效果,相信本文所建立的时间序列预测模型一定程度上可以进行产品需求的精准预测。
文章引用
唐玮煜,黄鸿亮,杨俊涛. 基于季节性ARIMA模型的新零售精准预测
Accurate Forecast of New Retail Based on Seasonal ARIMA Model[J]. 计算机科学与应用, 2020, 10(11): 2077-2088. https://doi.org/10.12677/CSA.2020.1011219
参考文献
- 1. 王正沛, 李国鑫. 消费体验视角下新零售演化发展逻辑研究[J]. 管理学报, 2019, 16(3): 333-342.
- 2. 张利. 基于时间序列ARIMA模型的分析预测算法研究及系统实现[D]: [硕士学位论文]. 镇江: 江苏大学, 2008.
- 3. 高惠璇. 应用多元统计分析[M]. 北京: 北京大学出版社, 2005.
- 4. 佘梓航, 徐嘉桦, 姚志玉, 梁伟典. 基于皮尔逊相关系数的网购大数据分析——以天猫佰润居旗舰店交易记录为例[J]. 韩山师范学院学报, 2020, 41(3): 16-22.
- 5. 刘胤池, 李庶林, 陈煌煜, 等. 基于ARIMA-SVM模型的深基坑变形预测及应用研究[C]//中国力学学会结构工程专业委员会. 第29届全国结构工程学术会议论文集(第II册). 武汉: 《工程力学》杂志社, 2020.
- 6. 王燕. 时间序列分析: 基于R [M]. 北京: 中国人民大学出版社, 2015.
- 7. 孙红果, 邓华. 样本自相关系数与偏自相关系数的研究[J]. 蚌埠学院学报, 2016, 5(1): 35-39.
- 8. 纪安之, 杨雪梅. 基于ARIMA模型的新冠肺炎序列分析预测[J]. 价值工程, 2020, 39(18): 107-109.
- 9. 沈齐, 范馨月. 季节性ARIMA接警量预测模型在警情分析中的应用[J]. 中国刑警学院学报, 2020(4): 57-61.
NOTES
*共同一作。
#通讯作者。
