Computer Science and Application
Vol.
14
No.
01
(
2024
), Article ID:
80318
,
15
pages
10.12677/CSA.2024.141017
图数据领域的频繁项集挖掘
邱文韬,兰红
江西理工大学信息工程学院,江西 赣州
收稿日期:2023年12月26日;录用日期:2024年1月24日;发布日期:2024年1月31日

摘要
本文对图数据中的频繁子图挖掘算法进行了综述。追溯了从传统非图数据频繁项集挖掘技术到图数据频繁子图挖掘的演化,详细阐述了经典算法如类Apriori方法和gSpan算法的原理与应用。也对近年来兴起的基于图表示学习的先进算法,如SPMiner、NSIC、LSS和NeurSC进行了系统的介绍和比较。本文不仅回顾了算法的历史演进,还对各类算法进行了详细的分析与讨论,通过分析这些算法的性能和特点,揭示了它们的优势与局限。最后,展望了图神经网络在频繁子图挖掘领域的未来发展方向,并指出了这些技术在生物网络分析、社交网络分析等领域应用的广阔前景。
关键词
频繁项集挖掘,图数据,频繁子图,图神经网络,机器学习

Frequent Itemset Mining in the Graph Data Field
Wentao Qiu, Hong Lan
School of Information Engineering, Jiangxi University of Science and Technology, Ganzhou Jiangxi
Received: Dec. 26th, 2023; accepted: Jan. 24th, 2024; published: Jan. 31st, 2024

ABSTRACT
We present a comprehensive review of frequent subgraph mining algorithms in graph data. We trace the evolution from traditional frequent itemset mining techniques for non-graph data to the current state-of-the-art in frequent subgraph mining for graph data, elaborating on the principles and applications of classic algorithms such as Apriori-like methods and the gSpan algorithm. We also systematically introduce and compare recent advanced algorithms that have emerged from graph representation learning, including SPMiner, NSIC, LSS, and NeurSC. We not only recount the historical progression of these algorithms but also provide a detailed analysis and discussion of each category. By examining their performance and characteristics, we reveal their advantages and limitations. Finally, we anticipate the future trajectory of graph neural networks in the field of frequent subgraph mining and highlight the vast potential for these technologies in applications like biological network analysis and social network analysis.
Keywords:Frequent Itemset Mining, Graph Data, Frequent Subgraphs, Graph Neural Networks, Machine Learning

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
频繁项集挖掘FIM (Frequent Itemset Mining)是最重要的数据挖掘任务之一,是关联规则挖掘、聚类、离群点分析等众多数据挖掘任务的基础 [1] 。自从它被提出以来,受到了越来越多的关注。图数据领域的频繁项集挖掘一般指的是频繁子图挖掘,即寻找在图数据集中频繁出现在各个图数据中的子结构。其在社交网络分析、生物信息学研究、交通网络以及图像识别等各个领域得到了广泛的应用,重要性不言而喻。
2. 频繁项集与频繁子图
频繁项集是在给定数据集中频繁出现的项的集合,而频繁子图是在图数据中频繁出现的子图。支持度被用来衡量项集或子图的重要性,频繁项集和频繁子图定义为支持度超过预设阈值的项集或子图。后文将对上述内容以及频繁子图挖掘的目标和瓶颈进行探讨。
2.1. 频繁项集
根据Han [2] 等,首先给出关于频繁项集的形式化定义:
Definition 2.1 (项集):项的集合称为项集(Itemset),包含k个项的项集称为k-项集。
Definition 2.2 (支持度):项集的支持度(Support)是一个项集在数据中的出现频率。
Definition 2.3 (频繁项集):频繁项集(Frequent Itemset)是根据用户自行设定最小支持度阈值minsup,支持度大于minsup的项集称为频繁项集。
2.2. 频繁子图
有了前述频繁项集的相关定义,相应的,可以给出频繁子图的相关概念:
Definition 2.4 (子图):图 是另一个图 的子图,如果它的顶点集 是 的子集,并且它的边集 是 的子集。子图关系记作 。
Definition 2.5 (子图的支持度):给定图的集族 ,子图 的支持度为包含它的所有图所占的百分比即
(1)
Definition 2.5 (频繁子图挖掘):给定图的集合 和支持度阈值 ,频繁子图挖掘的目标是找出所有使得 的子图 。
2.3. 频繁子图挖掘
频繁子图挖掘需要找到一个图中出现次数最多的大小为 的子图。这需要解决两个问题:i、是枚举出所有大小为 的连通子图,ii、统计不同类型的子图的个数。要解决这个问题很困难,因为仅确定一个特定子图是否存在于图中就已是计算代价很高的问题 [3] ,计算用时随子图大小指数级增长,因此传统方法可行的子图尺寸都相对较小。这也是为什么要使用GNN或者基于学习的方法,来帮助我们找到频繁子图,具体的解决方案是用控制搜索空间来解决组合爆炸的问题,然后用GNN来解决同构子图匹配的问题。问题形式化定义为:假设需要操作的图是 ,需要挖掘的子图的大小是 ,并且得到的结果为 。算法的目标是找到 中所有节点个数为 的子图并得到出现最高的频率。
2.4. 频繁子图挖掘的复杂度
因为具有指数级别的搜索空间,所以挖掘频繁子图的计算量很大。考虑包含 个实体的数据集,在频繁项集挖掘中,每个实体是一个项,搜索空间大小为 ,这是可能产生的候选项集的个数。在频繁子图挖掘中,以无向连通图为例,每个实体是一个顶点,并且最多可以有 条到其他顶点的边。假定顶点
的标号是唯一的,则子图的总数为 其中, 是选择 个顶点形成子图的方法数,而 是
子图的顶点之间边的最大值。Han等 [2] 给出了不同实体个数下项集与子图的数量,见表1。
Table 1. Comparison of the number of different dimensions d, itemsets and subgraphs
表1. 不同维度d,项集和子图个数的比较
3. 频繁项集生成的经典算法
频繁项集生成是数据挖掘中关联规则挖掘的一个重要步骤。经典的频繁项集生成算法主要包括Apriori算法和FP-growth算法,并且这两个算法的思想也延伸至频繁子图挖掘中,在此简要介绍一下这两个算法的主要思想。
3.1. APriori算法
APriori算法是一个经典的频繁项集挖掘算法,在1994年由IBM研究员Agrawal [4] 提出,它的核心思想是:广度优先搜索,自底而上遍历,逐步生成候选集与频繁项集,它基于一个重要的原理——反单调性原理(Antimonotonicity),其定义如下:
Definition 3.1 (反单调性):如果一个项集是频繁的,则它的所有子集一定也是频繁的。即 。
其中 表示支持度,依据该性质,对于某 项集,只要存在一个k项子集不是频繁项集,则可以直接判定该项集不是频繁项集。算法步骤主要分为连接步和剪枝步。连接步:从频繁 项集生成候选K项集(K ≥ 2)。具体来说,对于两个频繁 项集I和J,如果它们的前 个元素相同,那么可以将它们合并成一个候选K项集 。剪枝步:从候选K项集中筛选出频繁K项集。具体来说,对于每个候选K项集C,检查它的所有 子集是否都出现在频繁 项集中,如果有任何一个子集不是频繁的,则可以将C剪枝掉。
3.2. FP-Growth算法
FP-Growth算法也是一个经典的频繁项集挖掘算法,于2000年由韩家炜等提出 [5] 。它的核心思想是构造一棵能够压缩原始数据的频繁模式树(Frequent Pattern Tree, FP-Tree),成功构造FP树后,就可以使用递归的分治方法来挖掘频繁项集。
4. 经典的频繁子图挖掘算法
Akihiro Inokuchi等人 [6] 最早将Apriori算法思想应用到频繁子图挖掘中,引起了诸多学者对频繁子图挖掘的注意,各种算法也就应运而生 [7] ,韩家炜等人提出了将FP-Growth思想应用到子图挖掘中 [8] ,使得频繁子图挖掘算法得到了迅速发展。后来,许多研究人员,如Jun Huan等人提出了FFSM [9] 等基于FP-Growth思想的算法,使得频繁子图挖掘算法得到了进一步的发展。
基于贪心的方法,基于贪心策略的频繁子图挖掘是频繁子图挖掘领域最先发展起来的技术之一,其中最著名的是SUBUE算法 [10] ,SUBUE算法基于最小描述长度原则(Minimum Description Length, MDL)来发现子结构。
基于归纳逻辑编程(Inductive Logic Programming, ILP)的方法,其优点在于大多算法能找出出现频率高的子图,且能作为交好的类识别器。但其缺点在于不能保证发现所有的频繁子图。1998年Dehaspe基于ILP提出可对频繁子图进行完全挖掘的WARMR算法 [11] ,其算法核心思想与Apriori算法类似。
基于Apriori的方法——AGM算法,AGM算法在效率上与采用了分层搜索的ILP算法架构相比有了比较大的提升,而且在化学分子结构这样的真实世界图数据中也有不错的表现。但是其在判断模式图X和Y是否具有相同子图时,仍要花费较多时间。且每添加一个顶点产生新候选频繁子结构时,会产生许多冗余的k + 1顶点的子结构。
对Apriori方法的改进——FSG算法 [12] ,FSG是AGM算法的一种改进。同基于Apriori的方法一样,其采用了分级扩展的方法。FSG算法对AGM算法的优化主要体现在其采用了基于边的候选频繁子图生成方法,效率有所提升。不过仍产生了冗余的候选模式子图,所以仍需进行规范化判断。
基于模式增长的方法——gSpan (Graph-Based Substructure Pattern Mining)算法,Xifeng Yan [13] 提出的gSpan算法通过对图进行深度优先搜索遍历来发现频繁子图,解决了AGM和FSG算法基于Apriori逐层推进的方法所遇到的两个瓶颈:i、从k阶频繁子图构造k + 1阶频繁子图相当复杂且代价昂贵。ii、因为子图同构测试是一个NPC问题,所以处理误报的代价也是极其昂贵。
混合型方法——FFSM (Fast Frequent Subgraph Mining)算法 [14] [15] ,快速频繁子图挖掘FFSM采用了垂直搜索模式,通过解决潜在的子图同构问题并减少冗余候选子图的生成,大大提升了效率。
4.1. 类Apriori方法
类Apriori方法参考了Apriori的思想,基于频繁项集的概念,通过迭代的方式逐步生成频繁项集,并利用支持度计算和候选剪枝来提高算法效率,主要有四个步骤。
4.1.1. 步骤一:候选产生
在候选产生阶段,合并(k − 1)子图为k子图,首要问题是如何定义子图的大小k。通过添加一个顶点,迭代地扩展子图的方法称作顶点增长(Vertex Growing)。k也可以是图中边的个数,添加一条边到已有的子图中来扩展子图的方法称作边增长(Edge Growing)。
为了避免产生重复的候选,我们可以对合并施加条件:两个(k − 1)子图必须共享一个共同的(k − 2)子图,共同的子图称为核(Core)。由此,产生了两种子图候选产生的方法:1、顶点增长(Vertex Growing):过添加一个新的结点到已经存在的一个频繁子图上来产生候选。2、边增长(Edge Growing):增长将一个新的边插入到一个已经存在的频繁子图中。与顶点增长不同,结果子图的顶点个数不一定增长。
4.1.2. 步骤二:候选剪枝
候选剪枝需要剪去(k − 1)子图非频繁的候选。可以通过以下方式实现:相继从k子图中删除一条边,并检查得到的(k − 1)子图是否连通且频繁。如果不是,则该候选k子图可以丢弃。意思是一次删除一条,总共有k个子图要检测。
为了检查(k − 1)子图是否频繁,需要将其与其他的(k − 1)子图匹配,此时需判定两个图是否拓扑等价,即处理图同构的问题,图同构的定义如下。
Definition 4.1 (图的同构):对于给定的两个图 ,如果存在一个定义在 双射函数f满足对于 ,那么就称这两个图是同构的(Isomorphism)。图1是一个图同构示例,顶点之间并没有颜色区分,为了更好地看出顶点间的映射关系,加上了颜色。

Figure 1. Schematic diagram of graph isomorphism
图1. 图同构示意图
Definition 4.2 (子图同构):在无向图 和 中, 中的一个子图 可以通过一一映射 的方式对应到 中的一个子图 ,且在这个映射中,边的连接关系保持不变。如果这样的映射f存在,则称 和 是同构的,表示为: 。图2是一个子图同构示例,如果图G1和图G2的子图是同构的,就称G2关于G1是子图同构的,也可以说G1是G2的子图。
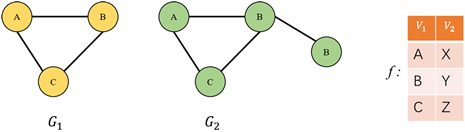
Figure 2. Schematic diagram of subgraph isomorphism
图2. 子图同构示意图
4.1.3. 步骤三:支持度计算
当剪枝完成之后,将剪枝后剩余的候选图进行支持度计算,将其中大于支持度阈值的候选图记为满足条件的频繁子图,支持度的计算见公式1。
4.1.4. 步骤四:候选删除
丢弃支持度小于minsup的所有候选子图,对于所有频繁的候选子图,还需要进行图的同构测试,以减除重复的频繁候选子图。
4.2. gSpan算法
AGM和FSG算法都采用了基于Aporiori逐层推进的方法,为了解决Aporiori模式会遇到的瓶颈,Xifeng Yan于2003年提出了gSpan (Graph-Based Substructure Pattern Mining)算法,通过对图进行深度优先搜索(DFS)遍历来发现频繁子图。gSpan算法在挖掘频繁子图的时候,用了和FP-Growth中相似的原理,即模式增长(Pattern-Grown)的方式,深度遍历及生成的DSF树示例见图3,挖掘的过程中同样没有产生候选集,也用到了最小支持度计数作为一个过滤条件。要了解gSpan算法,首先要了解几个概念:最右顶点与最右路径、前向边与后向边以及DFS编码。
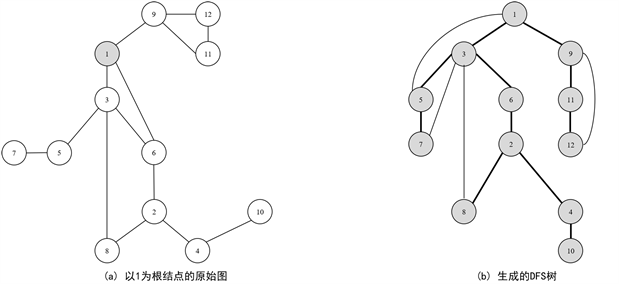
Figure 3. Depth-First Search graph traverses and the resulting DFS tree
图3. 图的深度遍历及生成的DFS树
4.2.1. 最右顶点与最右路径
gSpan在构建深度搜索树对图进行深度优先遍历,所有节点根据发现时间排序,其中 为根,最后发现的节点叫做最右节点 ,从第一个节点 到最右节点 的路径叫做最右路径。
4.2.2. 前向边与后向边
基于节点先后发现的顺序,每条边可以表示为(i, j),如果为前向边,则i < j,反之为后向边i > j。
4.2.3. DFS编码
根据前述,每个节点都有一个标记,则DFS编码可以将具有标记的图转化为边序列,每个边(DFS Code)用一个五元组表示: 。即(节点i的访问次序标记,节点j的访问次序标记,节点i的标签,边的标签,节点j的标签)。边的排序:假设有两条边 ,分别是两个五元组。如果满足 ,那么他们符合下述情况之一:a) 和 都是前向边,并且 ;b) 和 都是后向边,并且( 或者 且 );c) 是前向边, 是后向边,并且 ;d) 是后向边, 是前向边,并且 。
根据边的次序得到的边序列是图的DFS编码。图4(b)~(d)是由图4(a)得到DFS树示例,表2是其对应的DFS Code,显然深度优先搜索树是不唯一的,所以DFS Code也是不唯一的。
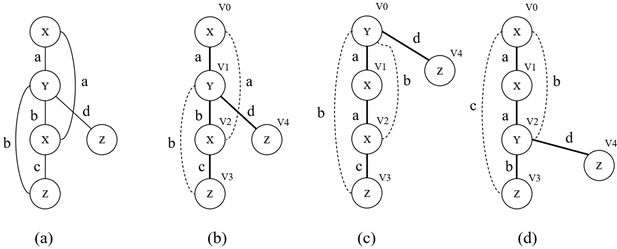
Figure 4. Depth-first search tree
图4. 深度优先搜索树表
Table 2. DFS Code for the DFS tree
表2. DFS树对应的DFS Code
将DFS序列定义为 。对于给定图G的DFS树T的集合,其有对应的DFS序列集Z: 。其中, 表示图G的DFS树T的编码。DFS序列是指将所有DFS树的编码按某种顺序排列形成的序列。可以对给定图G的DFS序列集 找到图G的最小DFS序列,也即 ,定义为图G的规范化标签。由此,两个图 与 同构当且仅当 。
gSpan算法通过这样的定义构造,将寻找频繁子图的问题转化为相应的最小DFS序列的问题,而这样的序列模式挖掘问题可以用已有的序列模式挖掘算法解决。简要来说,gSpan算法的流程就是,在得到 阶频繁子图的DFS编码树后,对其进行最右路径扩展。每次增加一条边,产生k + 1阶候选频繁子图。若k + 1阶候选频繁子图具有最小DFS序列(即规范化标签 ),则将其保留,否则丢弃该候选子图。而在计算k阶频繁子图的支持度 的时候,记录频繁子图的所有嵌入。由此,k + 1阶候选频繁子图的支持度 即可通过k阶频繁子图的嵌入进行最右扩展而计算得到。通过这种方法,gSpan算法可以有效地挖掘频繁子图。与Apriori算法和FP-Growth算法不同,gSpan算法使用DFS编码树来表示子图,通过最小化DFS序列来剪枝,从而提高了算法的效率。
4.3. 总结和比较
鉴于篇幅所限,本文重点讨论两种传统频繁子图挖掘算法:一种是具有里程碑意义的基于Apriori原理的方法,另一种是创新性的gSpan算法。从SUBDUE算法的贪心策略出发,通过整数线性规划(ILP)的应用,再到A. Inokuchi等人依据Apriori原理提出的AGM算法,我们见证了频繁子图挖掘效率的逐步提高。FSG算法对AGM算法在图表示和候选频繁子图生成过程中进行了改进,增强了效率并降低了资源消耗,虽然改善幅度有限。然而,真正的飞跃出现在gSpan算法中,这是一种模式增长方法,它巧妙地采用了深度优先搜索(DFS)策略,并通过定义DFS序列来有效避免冗余频繁子图的生成,这一策略显著提升了挖掘效率并节约了空间资源。FFSM算法进一步解决了Apriori基算法面临的两个主要挑战:子图同构问题和冗余候选子图的生成问题。通过采用一系列精细化策略,FFSM算法显著提高了效率。
如文献 [16] 所示,除了上述基于组合优化的方法,还有多种枚举 [17] [18] [19] 和分析方法 [20] [21] [22] 。枚举方法通过穷举所有子图来进行计数,枚举方法依靠子图同构检测来确定特定的查询图是否存在于目标数据图中,然而,子图同构被证明是NP完全问题 [23] [24] ,这大大限制了其效率。分析方法则是将大图分解成更小的子图进行计数,并依据这些小图的计数结果来推算大图的计数,分析方法专门设计用来处理某些特定大小的查询图,比如包含5个节点的查询图 [25] 。还有一些精确的子图计数算法 [26] 能够支持最多包含6个节点的查询图,这些算法往往难以扩展到任意大小和形状的查询图,因此在实际应用中的适用性受到限制。但这些算法的发展和优化,为频繁子图挖掘领域的进步提供了坚实的基石。
5. 基于学习的频繁子图挖掘算法
鉴于子图计数在许多领域的重要性、普遍性,以及其难以处理的特性,比如即便是精确的子图匹配计数方法,在处理百万级别的社交网络图频率挖掘问题时,也可能需要超过一周的时间来解决 [27] 。因此近年来,研究人员提出了基于学习的近似子图计数方法 [28] - [32] 。这些研究探索了神经网络在子图计数任务中的应用潜力,并证实了其可以取得显著成效。尽管如此,由于神经网络本身的复杂性,这些方法在可扩展性和效率方面仍存在挑战。尽管有这些挑战,这些基于学习的方法能够在较大规模的图上进行子图计数,从而在多种场合下得到了广泛应用。
5.1. 图神经网络
GNN (Graph Neural Network)是深度学习在图结构上的一个分支,由Scarselli等人在2009年第一次正式提出 [33] 。图中的一个节点可以通过其特征和相关节点进行定义,GNN的目标是学习一个状态嵌入 用于表示每个节点的邻居信息。状态嵌入 可以生成输出向量 用于作为预测节点标签的分布等。GNN由一系列GNN层线性组合构成,而GNN层的本质为:消息(Message) + 聚合(Aggregation),当我们训练一个GNN的时候可以从监督学习的视角出发进行训练,也可以从非监督学习的视角出发进行训练。GNN的总体框架分别包括:(1)消息与(2)聚合,也就是一个网络层中的操作,(3)层与层之间的连接(Layer Connectivity),(4)图增广(Graph Augmentation)与(5)学习目标(Learning Object)。
5.2. 神经子图匹配
5.2.1. 节点锚定
通过节点锚定(Node-Anchored)的方法将子图匹配问题转化成一个二分类问题,即用True和False来判断一个图是否同构于另一个图的子图,首先用GNN去计算两个图中对应节点 和 的嵌入向量,然后来判断 的邻居节点和 的邻居节点是不是同构的。假设我们需要在图 中匹配一个子图 ,首先对每个节点计算出K-Hop邻居,可以使用BFS等进行计算,K为超参数,可以自行设定。然后使用GNN得到邻居的嵌入向量。这种方法不仅可以判断是不是子图,还可以同时标定一组对应的点。
5.2.2. 有序嵌入空间
子图同构关系可以在有序嵌入空间中很好地编码,其具有i、传递性,A是B的子图,B是C的子图,那么A是C的子图;ii、反对称性,如果AB互为子图那么他们同构;iii、闭包性,单个节点的图是所有非空图的子图,空节点是所有图的子图。这些性质为将一个图结构嵌入到一个有序嵌入空间中提供了支持。将图 映射到高维空间中的一个点,并使得这个点的所有维度都是非负的,空间内的嵌入向量就可以比较大小。
5.2.3. 模型构建与训练
用锚点和有序嵌入的方式可以解决子图同构问题 [34] ,在向量空间中可以使用图神经网络进行子图匹配,图5是一般情况下的神经子图匹配过程,为了构建并训练一个完整的模型,需要设定一个损失函数,来学习反映出子图关系的嵌入向量。损失函数的设定需要满足有序约束,这种约束可以保证子图关系的
信息在嵌入空间中被保留了,通常设置损失函数为: 。 是两个
待判断的图, 是嵌入空间的点数, 分别是图 和图 第 个点的嵌入表达。对于有子图关系的两个图来说就是 值为0,否则为一个正数。可以采用负采样的方式来训练模型,对于样本选取一半为有子图关系的正样本,而另一半为没有子图关系的负样本,并且使用一个max-margin损失函数,即对于正样本,最小化 ;对于负样本,最小化 , 为自行设定的margin,负样本计算出的惩罚函数越小则距离正确的位置越近。
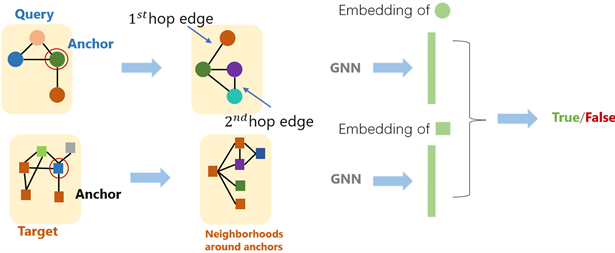
Figure 5. Neural subgraph matching
图5. 神经子图匹配
5.3. SPMiner算法
SPMiner (Subgraph Pattern Miner) [35] 是第一个近似识别频繁子图的神经网络方法,由斯坦福大学在2020年提出,其优于现有的启发式 [36] [37] 和基于搜索的近似算法 [38] [39] ,斯坦福大学通过实验证明该方法能够挖掘出 频繁子图,而相同情况下非学习的方法只能挖掘出 的频繁子图,其算法过程如图6所示。它包括两个步骤:一个用于嵌入子图的编码器和一个模式搜索过程。SPMiner和前面所述的子图匹配神经网络是一致,创新点在最后一步“Search Procedure”。Search Procedure是一个递归的过程,第一次迭代时找出一个节点anchor (一个节点是任意图的子图),然后找出anchor直接相连的节点,使得这两个节点构成的子图为目标图的最高频子图(size = 2);第二次迭代则是找出与上一步两个节点直接相连的一个节点,使得这三个节点构成的子图为目标图的最高频子图(size = 3);依次执行,直到迭代k次,这样就找出一个由k个节点构成的最高频子图。在几个真实世界的数据集上,SPMiner在给定所需子图大小的情况下寻找频繁子图方面优于流行的非神经基线和多层感知器(MLP)基线,从而更好地处理搜索空间的组合爆炸。
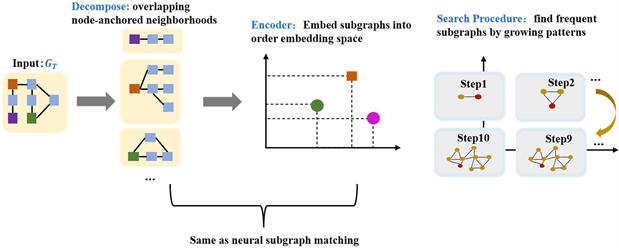
Figure 6. Schematic diagram of the SPMiner algorithm
图6. SPMiner算法示意图
5.4. NSIC算法
Neural Subgraph Isomorphism Counting (NSIC)是首个用GNN来做子图同构统计的方法,主要解决的问题是给定一个小图(pattern)和一个大图(graph),统计graph中与pattern同构的子图数量,GNN的优势在于能够在可接受的误差范围内以更快的速度解决这个问题,NSIC由Xin Liu [40] 等人在2020年提出。
在NSIC框架中,将图G作为包含信息的数据,将模式P作为从图中检索信息的查询。因此,计数问题可以自然地被表述为自然语言处理中已经建立起来的问答问题。除了文本和图作为输入的差异外,主要问题在于在问答模型中,答案通常是从提供的文本中提取出的事实,而在计数问题中,答案是匹配的局部模式的汇总统计信息。为了使问题可学习,图(或模式)应该被表示为一系列边或一系列相邻矩阵和
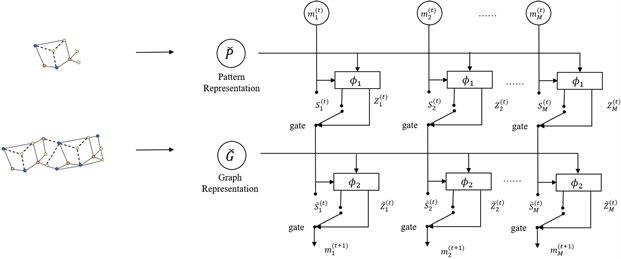
Figure 7. DIAM structure of NSIC
图7. NSIC使用的DIAM网络结构
顶点特征。NSIC为序列模型和图模型提供了通用的编码方法。创新点在于引入了一个Dynamic Intermedium Attention Memory (DIAMNet)来解决计数的更全局的推理问题,DIAM网络结构如图7所示。结果表明,NSIC比传统算法VF-2快10~1000倍,误差在可接受的范围内。
5.5. LSS算法
A Learned Sketch for Subgraph Counting (ALSS)是由Kangfei Zhao [41] 等人在2021年提出的主动学习子图计数的方法。ALSS主要由两部分组成:
1、Sketch Learned(LSS):利用神经网络训练一个回归模型。主要步骤有:i、将查询图q分解为一些更小的子结构。Ii、提取子结构的特征,用定长的向量表示。Iii、通过聚合所有子结构的表示来得到Q图的匹配数。LSS有两个学习任务:1、给定查询图q预测子图匹配数;2、帮助AL决定如何为未来学习选择测试的查询图q。
2、Active Learner (AL):由于不可能得到完全的训练集来供模型学习,所以需要AL模块来学习一个策略,这个策略能基于模型目前的信息量,从未标注数据池中选择一些数据,来扩充训练数据以提升模
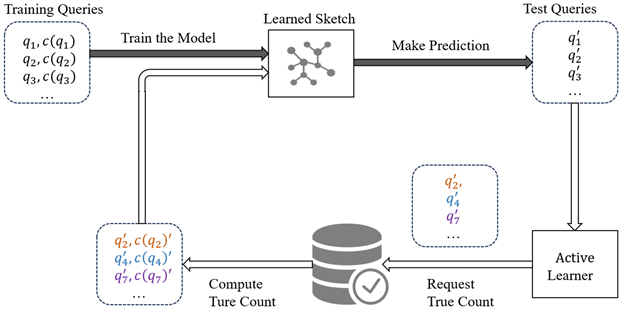
Figure 8. Overview of the Active Learned Sketch
图8. Active Learned Sketch架构
型效果。AL利用了分类任务的不确定性和关联任务的一致性,无需做梯度计算。相比于消极学习,AL的目的是在同样的数据量下,训练出更好的模型。
ALSS的架构如图8所示,LSS的设计灵感来自基于分解的子图计数。首先将查询图分解为更小的子结构,计算/估计分解后的子结构的计数,并将分解后的各个子结构的计数聚合为最终结果。ALSS相较于以前的模型速度更快,而且错误率更低,成本比传统方法低3个数量级。但它与大部分基于学习的方法一样,只能用于模糊计数。
5.6. NeurSC算法
Neural Subgraph Counting with Wasserstein Estimator (NeurSC)由Hanchen Wang [42] 等人于2022年提出,NeurSC由一个自适应提取模块和一个估计器组成,可以高效地从查询和数据图中提取和组合信息,NeurSC的算架构如图9所示。NeurSC的估计精度通过Wasserstein Estimator得到改进,通过更新网络参数、查询和数据图之间的顶点对应关系,最小化了查询和数据图之间的Wasserstein距离。
NeurSC的算法框架主要包括以下步骤:从查询图和数据图中提取信息并构建子图。利用Wasserstein 判别器进行对抗训练并提高图的表示和估计精度。将子图集成到估计器中,计算估计值。
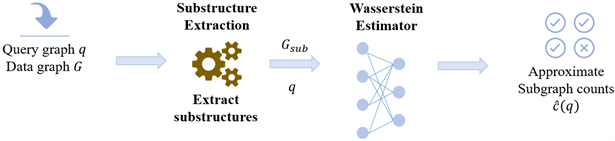
Figure 9. NeurSC algorithm architecture
图9. NeurSC算法架构
NeurSC的模块会自适应从查询图和数据图中提取子结构,以减少不利数据顶点的影响和提高模型的效率和可扩展性。然后,估计器将有效地组合查询和数据图的信息。最后,通过以Wasserstein判别器为基础的对抗训练提高了估计精度和质量。在七个大型真实标记图上的实验结果表明 [24] ,NeurSC在预测精度和鲁棒性方面优于NSIC和LSS。
5.7. 总结和比较
SPMiner引入了一种强大的图神经网络编码器,其表达能力使得它能够有效地捕捉图结构的复杂性。然而,这种能力的背后是它的计算成本,因为这种编码器本质上是复杂且计算密集的。SPMiner特别依赖于一个有序的嵌入空间,以此来捉捕图在子图层级关系中的偏序特征。这意味着,如果嵌入空间的学习不够精确,它在子图识别的准确性上可能会受到影响。而对于庞大的图,要求更高维度的嵌入空间以维持性能,这进一步增加了SPMiner在计算复杂性、嵌入质量依赖性以及扩展性方面的挑战。与SPMiner相似,NeuroMatch (2020年提出) [43] 和LMKG (2021年提出) [44] 等算法,主要致力于解决子图包含问题,即判断一个给定的查询图是否为一个更大数据图的子图。这些方法将查询的存在与否视为一个二分类问题,但它们并不适合直接应用于子图计数问题,后者通常被看作是一个回归问题。
在子图计数的其他方法中,LSS、NSIC和NeurSC与SPMiner有所区别。SPMiner无需预设查询图,而是直接在数据图中识别频繁出现的子图。相比之下,LSS、NSIC和NeurSC主要关注统计特定查询图在数据图中的出现频率。在NSIC出现之前,子图同构计数问题通常依赖于如Ullmann算法 [45] 这样的精确算法,这些算法在计算上非常复杂,不适合处理大型数据集。NSIC由于编码了完整的查询图和数据图,参数空间大,导致在大数据图上其子图计数结果可能完全由数据图的结构所主导,有时甚至无法区分出查询图,限制了它处理的数据图的规模,通常仅限于顶点数为上千级别的数据图。
在LSS出现之前,过去的方法在支持同构子图计数和未标记图的小查询图子图计数方面能力有限,无法很好地适应结构不规则的数据和查询图。LSS采取主动学习策略,基于模型的信息量选择无标记数据集的子集,旨在提高预测的准确性并降低计算成本。然而,它存在两个主要限制:一是LSS仅在查询图的子结构上应用图神经网络,没有充分利用数据图的信息;二是LSS中的参数k (代表从每个查询顶点开始的k跳广度优先搜索距离)是固定的,可能导致所有生成的子结构与查询图相同,影响效率和准确性。
NeurSC旨在通过更有效地提取和利用数据图和查询图中的信息来克服LSS和NSIC的局限性,提升子图计数任务的效率和精度。尽管如此,NeurSC的性能在很大程度上依赖于从数据图中提取的候选子结构的质量。如果这些子结构的代表性不足,估算的准确性可能会下降。此外,NeurSC所依赖的Wasserstein鉴别器需要查询图和数据图之间的顶点对应信息,这在某些特定图结构中可能难以获得,从而限制了其应用范围。
6. 总结
本文以非图数据的频繁项集挖掘为起点,拓展至图数据领域的频繁子图挖掘,深入剖析了该领域的关键算法和方法。文章集中讨论了基于Apriori原则的传统算法和革新性较强的gSpan算法,以及它们的发展与提升。从SUBDUE算法的贪心策略,到AGM和FSG算法在图表示和候选子图生成上的改良,本研究记录了挖掘效率与资源消耗优化的历程。值得注意的是,gSpan算法采用的模式增长方法和FFSM算法的细致策略,不仅显著提高了挖掘效率,还解决了子图同构和候选子图生成的关键难题。近年来,研究者们致力于探索新的路径,将频繁子图挖掘视为机器学习中的预测任务,尤其是基于表示学习的方法。本文详细考察了SPMiner在图神经网络方面的创新应用,以及LSS、NSIC和NeurSC等方法在子图同构计数问题上的新进展。同时,分析了这些方法在处理大规模数据集时所展现的潜力与面临的挑战,及其在特定情况下的局限性。随着图数据在现实世界应用的普及与增长,频繁子图挖掘领域的发展势头强劲,预计将在生物网络分析、社交网络分析、图像处理等多个领域展现广阔的应用潜力。计算能力的增强和算法的进步,使得频繁子图挖掘有望在未来解决更多实际问题。展望未来,图神经网络(GNN)作为处理图数据的关键技术,有望获得进一步的发展和完善,从而提升对图结构的建模能力和计算效率。类似于NeurSC中采用的自适应子结构提取方法,预计会有更多创新算法问世。随着对图数据分析需求的不断增长,我们可能会见证更多注重可解释性的图神经网络模型的涌现,以便更深入地理解和解释图数据分析的成果。这些技术进步和应用的不断展开,有望推动图数据分析领域的整体进步,为生物网络分析、社交网络分析、推荐系统等实际应用场景提供更为强大的分析工具和方法。
文章引用
邱文韬,兰 红. 图数据领域的频繁项集挖掘
Frequent Itemset Mining in the Graph Data Field[J]. 计算机科学与应用, 2024, 14(01): 158-172. https://doi.org/10.12677/CSA.2024.141017
参考文献
- 1. Agrawal, R., Imielinski, T. and Swami, A. (1993) Mining Association Rules between Sets of Items in Large Databases. Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data, Washington DC, 25-28 May 1993, 207-216. https://doi.org/10.1145/170035.170072
- 2. Han, J. and Kamber, M. (2012) Data Mining: Concepts and Techniques. Morgan Kaufmann, San Francisco.
- 3. Han, J. and Kamber, M. (2001) Applying the Aprio-ri-Based Graph Mining Method to Mutagenesis Data Analysis. Journal of Computer Aided Chemistry, 2, 87-92. https://doi.org/10.2751/jcac.2.87
- 4. Agrawal, R. and Srikant, R. (1994) Fast Algorithms for Mining Association Rules. Proceedings of the 20th International Conference on Very Large Data Bases, Santiago de Chile, 12-15 September 1994, 487-499.
- 5. Han, J., Pei, J. and Yin, Y. (2004) Mining Frequent Patterns without Candidate Generation: A Frequent-Pattern Tree Approach. Data Mining and Knowledge Discovery, 8, 53-87. https://doi.org/10.1023/B:DAMI.0000005258.31418.83
- 6. Inokuchi, A., Washio, T. and Motoda, H. (2000) An Apriori-Based Algorithm for Mining Frequent Substructures from Graph Data. Principles of Data Mining and Knowledge Discovery, Lyon, 13-16 September 2000, 13-23. https://doi.org/10.1007/3-540-45372-5_2
- 7. Inokuchi, A., Nishimura, T.K. and Motoda, H. (2002) A Fast Algo-rithm for Mining Frequent Connected Subgraph. IBM Research, Tokyo Research Laboratory, Tokyo.
- 8. Inokuchi, A., Washio, T. and Motoda, H. (2003) Complete Mining of Frequent Patterns from Graphs: Mining Graph Data. Machine Learning, 50, 321-354.
- 9. Jun, H.W., et al. (2004) Spin: Mining Maximal Frequent Subgraphs from Graph Databases. Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, 22-25 August 2004, 581-586.
- 10. Holder, L.B., Cook, D.J. and Djoko, S. (1994) Substucture Discovery in the SUBDUE System. AAAIWS’94: Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining, Seattle, 31 July-1 August 1994, 169-180. https://doi.org/10.1109/TKDE.2005.127
- 11. Deshpande, M., Kuramochi, M., Wale, N. and Karypis, G. (2003) Frequent Sub-Structure-Based Approaches for Classifying Chemical Compounds. IEEE Transactions on Knowledge and Data Engineering, 17, 1036-1050. https://doi.org/10.1109/TKDE.2005.127
- 12. Yan, X.F. and Han, J.W. (2002) gSpan: Graph-Based Substructure Pattern Mining. 2002 IEEE International Conference on Data Mining, Maebashi City, 9-12 December 2002, 721-724.
- 13. Kuramochi, M. and Karypis, G. (2001) Frequent Subgraph Discovery. Proceedings 2001 IEEE Interna-tional Conference on Data Mining, San Jose, 29 November-2 December 2001, 313-320.
- 14. Huan, J., Wang, W. and Prins, J. (2003) Efficient Mining of Frequent Subgraphs in the Presence of Isomorphism. 3rd IEEE International Con-ference on Data Mining, Melbourne, 22 November 2003, 549-552.
- 15. Nijssen, S. and Kok, J.N. (2004) A Quickstart in Frequent Structure Mining Can Make a Difference. Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, 22-25 August 2004, 647-652. https://doi.org/10.1145/1014052.1014134
- 16. Ribeiro, P., et al. (2021) A Survey on Subgraph Counting: Con-cepts, Algorithms and Applications to Network Motifs and Graphlets. ACM Computing Surveys, 54, Article No. 28.
- 17. Bhattarai, B., Liu, H. and Huang, H.H. (2019) CECI: Compact Embedding Cluster Index for Scalable Subgraph Matching. Proceedings of the 2019 International Conference on Management of Data, Amsterdam, 30 June-5 July 2019, 1447-1462. https://doi.org/10.1145/3299869.3300086
- 18. Bi, F., Chang, L.J., Lin, X.M., Qin, L. and Zhang, W.J. (2016) Efficient Subgraph Matching by Postponing Cartesian Products. Proceedings of the 2016 International Confer-ence on Management of Data, San Francisco, 26 June-1 July 2016, 1199-1214. https://doi.org/10.1145/2882903.2915236
- 19. Archibald, B., et al. (2019) Sequential and Parallel Solution-Biased Search for Subgraph Algorithms. 16th International Conference, CPAIOR 2019, Thessaloniki, 4-7 June 2019, 20-38. https://doi.org/10.1007/978-3-030-19212-9_2
- 20. Ahmed, N.K., Neville, J., Rossi, R.A. and Duffield, N. (2015) Efficient Graphlet Counting for Large Networks. IEEE International Conference on Data Mining, Atlantic City, 14-17 November 2015, 1-10. https://doi.org/10.1109/ICDM.2015.141
- 21. Ortmann, M. and Brandes, U. (2017) Efficient Orbit-Aware Triad and Quad Census in Directed and Undirected Graphs. Applied Network Science, 2, Article No. 13. https://doi.org/10.1007/s41109-017-0027-2
- 22. Melckenbeeck, I., Audenaert, P., Colle, D. and Pickavet, M. (2018) Efficiently Counting All Orbits of Graphlets of Any Order in a Graph Using Autogenerated Equations. Bioinformatics, 34, 1372-1380. https://doi.org/10.1093/bioinformatics/btx758
- 23. Bodirsky, M. (2016) Graphs and Homomorphisms. In: Schrö-der, B., Ed., Ordered Sets: An Introduction with Connections from Combinatorics to Topology, Springer International Publishing, Cham, 155-171.
- 24. Cook, S.A. (1971) The Complexity of Theorem-Proving Procedures. Proceedings of the 3rd Annual ACM Symposium on Theory of Computing, Shaker Heights, 3-5 May 1971, 151-158. https://doi.org/10.1145/800157.805047
- 25. Pinar, A., Comandur, S. and Vishal, V. (2017) ESCAPE: Efficiently Counting All 5-Vertex Subgraphs. Proceedings of the 26th International Conference on World Wide Web, Perth, 3-7 April 2017, 1431-1440. https://doi.org/10.1145/3038912.3052597
- 26. Zhang, H., Yu, J.X., Zhang, Y.K., Zhao, K.F. and Cheng, H. (2020) Distributed Subgraph Counting: A General Approach. Proceedings of the VLDB Endowment, 13, 2493-2507. https://doi.org/10.14778/3407790.3407840
- 27. Chen, X. and Lui, J.C. (2018) Mining Graphlet Counts in Online Social Networks. ACM Transactions on Knowledge Discovery from Data (TKDD), 12, Article No. 41. https://doi.org/10.1145/3182392
- 28. Chen, Z., Chen, L., Villar, S. and Bruna, J. (2020) Can Graph Neural Net-works Count Substructures? https://arxiv.org/abs/2002.04025
- 29. Bressan, M., Chierichetti, F., Kumar, R. and Leucci, S. and Panconesi, A. (2017) Counting Graphlets: Space vs Time. Proceedings of the 10th ACM International Conference on Web Search and Data Mining, Cambridge, 6-10 February 2017, 557-566. https://doi.org/10.1145/3018661.3018732
- 30. Bhuiyan, M.A., Rahman, M., Rahman, M. and Al Hasan, M. (2012) GUISE: Uniform Sampling of Graphlets for Large Graph Analysis. 2012 IEEE 12th International Conference on Data Mining, Brussels, 10-13 December 2012, 91-100. https://doi.org/10.1109/ICDM.2012.87
- 31. Bressan, M., Leucci, S. and Panconesi, A. (2019) Motivo: Fast Motif Counting via Succinct Color Coding and Adaptive Sampling. Proceedings of the VLDB Endowment, 12, 1651-1663. https://doi.org/10.14778/3342263.3342640
- 32. Wang, H., et al. (2022) Reinforcement Learning Based Query Vertex Ordering Model for Subgraph Matching. https://arxiv.org/abs/2201.11251
- 33. Scarselli, F., et al. (2009) The Graph Neural Network Model. IEEE Trans-actions on Neural Networks, 20, 61-80. https://doi.org/10.1109/TNN.2008.2005605
- 34. Leskovec, J., Kipf, T. and van der Maaten, L. (2023) CS224w: Machine Learning with Graphs. http://web.stanford.edu/class/cs224w/
- 35. Ying, R., Wang, A., You, J. and Leskovec, J. (2020) Frequent Subgraph Mining by Walking in Order Embedding Space. https://snap.stanford.edu/frequent-subgraph-mining/
- 36. Bonnici, V., Giugno, R., Pulvirenti, A., Shasha, D. and Ferro, A. (2013) A Subgraph Isomorphism Algorithm and Its Application to Biochemical Data. BMC Bioinformatics, 14, S13. https://doi.org/10.1186/1471-2105-14-S7-S13
- 37. Jüttner, A. and Madarasi, P. (2018) VF2++—An Improved Subgraph Isomorphism Algorithm. Discrete Applied Mathematics, 242, 69-81. https://doi.org/10.1016/j.dam.2018.02.018
- 38. Mhedhbi, A. and Salihoglu, S. (2019) Optimizing Subgraph Queries by Combining Binary and Worst-Case Optimal Joins. Proceedings of the VLDB Endowment, 12, 1692-1704. https://doi.org/10.14778/3342263.3342643
- 39. Shang, H.C., Zhang, Y., Lin, X.M. and Yu, J.X. (2008) Taming Verification Hardness: An Efficient Algorithm for Testing Subgraph Isomorphism. Proceedings of the VLDB Endow-ment, 1, 364-375. https://doi.org/10.14778/1453856.1453899
- 40. Liu, X., et al. (2020) Neural Subgraph Isomorphism Counting. Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 6-10 July 2020, 1959-1969. https://doi.org/10.1145/3394486.3403247
- 41. Zhao, K.F., Yu, J.X., Zhang, H., Li, Q.Y. and Rong, Y. (2021) A Learned Sketch for Subgraph Counting. Proceedings of the 2021 International Conference on Management of Data, 20-25 June 2021, 2142-2155. https://doi.org/10.1145/3448016.3457289
- 42. Wang, H., et al. (2022) Neural Subgraph Counting with Wasser-stein Estimator. Proceedings of the 2022 ACM SIGMOD International Conference on Management of Data, Philadelphia, 12-17 June 2022, 160-175. https://doi.org/10.1145/3514221.3526163
- 43. Ying, Z.T., Lou, Z.Y., You, J.X., et al. (2020) Neural Subgraph Matching. https://doi.org/10.48550/arXiv.2007.03092
- 44. Davitkova, A., Gjurovski, D. and Michel, S. (2021) LMKG: Learned Models for Cardinality Estimation in Knowledge Graphs. https://arxiv.org/abs/2102.10588
- 45. Ullmann, J.R. (1976) An Algorithm for Subgraph Isomorphism. Journal of the ACM, 23, 31-42. https://doi.org/10.1145/321921.321925
