Advances in Applied Mathematics
Vol.06 No.03(2017), Article ID:20792,9
pages
10.12677/AAM.2017.63042
p-Norm DSDD Matrices and New Eigenvalue Localization Region
Qiaojuan Zheng, Yaotang Li*
School of Mathematics and Statistics, Yunnan University, Kunming Yunnan
*通讯作者。

Received: May 6th, 2017; accepted: May 24th, 2017; published: May 27th, 2017

ABSTRACT
A new class of nonsingular matrices, p-norm double strictly diagonally dominant matrices, (shorthand for p-norm DSDD matrices), is presented, and it is used to get a new eigenvalue inclusion region. A numerical example is given to show that the eigenvalue inclusion in this paper, in some cases, is in the famous Brauer-Cassini oval area.
Keywords:p-Norm DSDD Matrix, Nonsingular H-Matrix, Eigenvalue Localization
p-范数双严格对角占优矩阵与新的矩阵特征值包含区域
郑巧娟,李耀堂*
云南大学数学与统计学院,云南 昆明

收稿日期:2017年5月6日;录用日期:2017年5月24日;发布日期:2017年5月27日

摘 要
给出一类新的非奇异矩阵——p-范数双严格对角占优矩阵(简记为p-范数DSDD矩阵),并由其得到一个新的矩阵特征值包含区域。文中算例表明在某些情况下本文的矩阵特征值包含区域含于著名的Brauer- Cassini卵形区域之中。
关键词 :p-范数DSDD矩阵,非奇异H-矩阵,特征值定位

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
矩阵特征值的包含区域在动力系统的稳定性分析,控制系统的可控制性研究,线性方程组的解法等问题的研究中有着重要的作用,是矩阵应用与分析中的一个重要课题。国内外许多学者都致力于这一问题的研究,无论是理论还是实用的需要,人们都希望用尽可能少的关于矩阵的信息与计算得到尽可能小的矩阵特征值包含区域以便更精确地定位矩阵特征值。本文继续矩阵特征值包含区域的研究,通过引进一类新的非奇异矩阵——p-范数DSDD矩阵,并由此给出一个新的矩阵特征值包含区域,在某些情况下改进了著名的矩阵特征值包含区域——Brauer-Cassini卵形区域。
首先给出文中所用的符号和术语。设n为自然数,记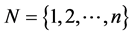 。q为正数或无穷大,记为
。q为正数或无穷大,记为 。设向量
。设向量 ,
, ,
, 。记
。记
 ,
,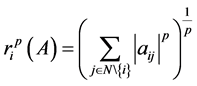 ,
, 。
。
特别地,(1) 当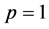 时,
时, ;(2) 当
;(2) 当 时,
时, 。
。
下面我们回顾文 [1] 中双严格对角占优(DSDD)矩阵的定义及其由此得到的矩阵特征值包含集。
定义1 [1] 。设 ,如果对所有
,如果对所有 ,且
,且 ,都有
,都有
 , (1.1)
, (1.1)
则称 为双严格对角占优矩阵,记为DSDD矩阵。
为双严格对角占优矩阵,记为DSDD矩阵。
定理1 [2] [3] [4] 。若 为双严格对角占优矩阵,则
为双严格对角占优矩阵,则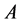 为非奇异的。
为非奇异的。
文献 [5] [6] 中给出了与双严格对角占优矩阵相对应的特征值包含区域:Brauer-Cassini卵形区域。
定理2 [5] [6] 。(Brauer定理)。设 ,则
,则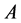 的所有特征值都包含在其
的所有特征值都包含在其 个Cassini卵形区域的并集之中,即
个Cassini卵形区域的并集之中,即
 (1.2)
(1.2)
其中 为
为 的谱(即
的谱(即 的所有特征值所成之集),
的所有特征值所成之集),
 ,
,
称为矩阵 的Cassini卵形区域。
的Cassini卵形区域。
2. p-范数DSDD矩阵
本节,我们引入一类新的非奇异矩阵:p-范数DSDD矩阵。为此先介绍p-范数SDD矩阵的定义 [7] 。
定义2 [7] 。设 ,
, . 若存在满足
. 若存在满足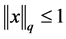 的正向量
的正向量 ,使得
,使得
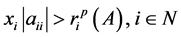 。 (2.1)
。 (2.1)
则称 为p-范数SDD矩阵,其中
为p-范数SDD矩阵,其中 为
为 的Hölder补,即
的Hölder补,即 。
。
定理3 [7] 。若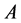 为p-范数SDD矩阵,则
为p-范数SDD矩阵,则 为非奇异的。
为非奇异的。
下面定理给出p-范数SDD矩阵的一个充分必要条件。
定理4 [7] 。设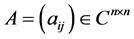 ,
, ,则
,则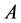 为p-范数SDD矩阵当且仅当
为p-范数SDD矩阵当且仅当
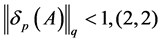 ,(2.2)
,(2.2)
其中,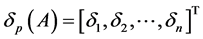 ,
, ,
, ,
, 为
为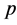 的Hölder补,即
的Hölder补,即 。
。
受定义1、定义2及定理1和定理3的启发,我们提出如下问题。设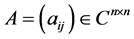 ,
, 。若
。若 满足
满足
 ,
, 。 (2.3)
。 (2.3)
那么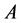 是否为非奇异的呢?很显然,当
是否为非奇异的呢?很显然,当 时,
时, 为双严格对角占优矩阵,则从定理1知,是非奇异的。那么,在一般情况下,即
为双严格对角占优矩阵,则从定理1知,是非奇异的。那么,在一般情况下,即 时,条件(2.3)式能保证
时,条件(2.3)式能保证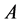 的非奇异性吗?我们先看如下例子。
的非奇异性吗?我们先看如下例子。
例1。设
 。
。
当 时,恒有
时,恒有 ,则
,则 满足
满足
 ,
, 。
。
但是,由于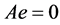 ,其中
,其中 ,则
,则 ,故
,故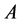 为奇异的。
为奇异的。
此例说明,一般来讲条件(2.3)式并不能保证矩阵 的非奇异性。因此要保证
的非奇异性。因此要保证 的非奇异性,仍需要添加一些条件。
的非奇异性,仍需要添加一些条件。
定理5。设 ,
, 。若存在满足
。若存在满足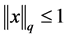 的正向量
的正向量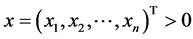 ,使得
,使得
 ,
, 。(2.4)
。(2.4)
则 为非奇异的,其中
为非奇异的,其中 为
为 的Hölder补,即
的Hölder补,即 。
。
证明:设 ,由(2.4)知
,由(2.4)知 。令
。令
 。
。
将它们从小到大排列为
 ,
,
则条件(2.4)等价于
 。
。
特别地,由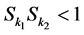 知
知 。若
。若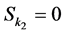 ,则
,则 。因此,
。因此,
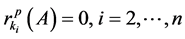 。
。
故 。若
。若 ,记
,记 ,则
,则 。令
。令
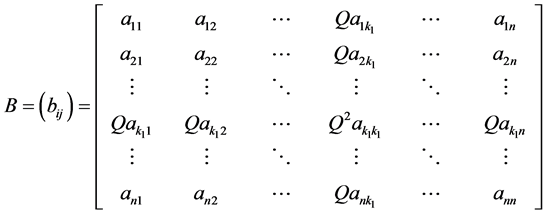 。
。
由于矩阵 表示
表示 乘上矩阵
乘上矩阵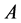 的第
的第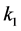 行,第
行,第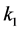 列后得到的矩阵,则
列后得到的矩阵,则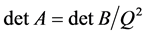 。因此,要证
。因此,要证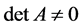 ,只需证
,只需证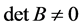 即可。对于矩阵
即可。对于矩阵 ,约定采用与
,约定采用与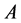 类似的记号,但都标以“'”以示区别。此时,有
类似的记号,但都标以“'”以示区别。此时,有
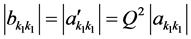 ,
, 。
。
于是,
 。
。
对于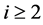 ,
,
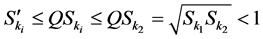 。
。
于是矩阵 满足定义2中的条件(2.1),故
满足定义2中的条件(2.1),故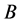 为p-范数SDD矩阵,再由定理3知
为p-范数SDD矩阵,再由定理3知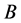 非奇异,即
非奇异,即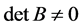 。 因此,
。 因此, ,则
,则 为非奇异的。
为非奇异的。
由定理5,我们可以给出p-范数DSDD矩阵的定义。
定义3。设 ,
, 。若存在满足
。若存在满足 的正向量
的正向量 使得(2.4)式成立,即
使得(2.4)式成立,即
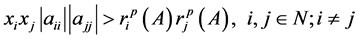 。
。
则称 为p-范数DSDD矩阵,其中
为p-范数DSDD矩阵,其中 为
为 的Hölder补,因此
的Hölder补,因此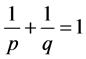 。
。
由定义3和定理5可直接得到如下定理。
定理6。设 为p-范数DSDD矩阵,则
为p-范数DSDD矩阵,则 非奇异。
非奇异。
下面我们给出p-范数DSDD矩阵的一个充分必要条件。
定理7。设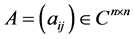 ,
, ,则
,则 为p-范数DSDD矩阵当且仅当
为p-范数DSDD矩阵当且仅当
 。 (2.5)
。 (2.5)
证明:记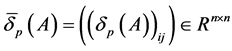 ,
,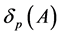 为其的按行拉直向量,即
为其的按行拉直向量,即
 ,
,
 ,
,
 。
。
这里 为向量
为向量 的q-范数,
的q-范数, 为
为 的Hölder补,即
的Hölder补,即 。
。
必要性,若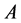 为p-范数DSDD矩阵,由定义3知,存在满足
为p-范数DSDD矩阵,由定义3知,存在满足 的正向量
的正向量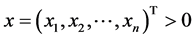 使得(2.4)式成立,即
使得(2.4)式成立,即
 ,
,
因此

充分性,设 且
且 ,即
,即
 。
。
则存在充分小的 ,使得
,使得
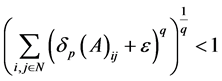 。
。
取

其中 满足对所有
满足对所有 ,
, ,则
,则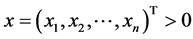 且
且
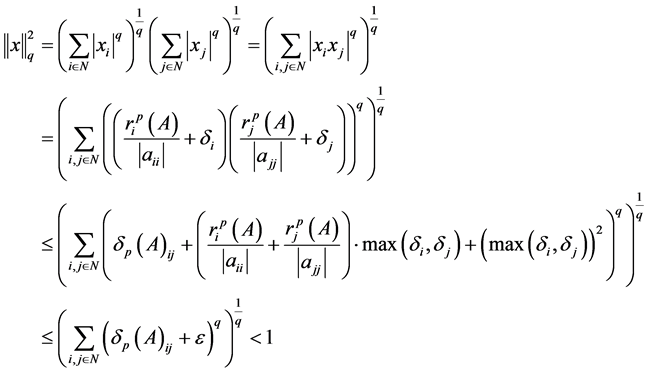 。
。
故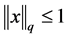 且
且
 。
。
即正向量 满足
满足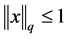 且能保证(2.4)式成立,故矩阵
且能保证(2.4)式成立,故矩阵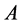 为p-范数DSDD矩阵。定理得证。
为p-范数DSDD矩阵。定理得证。
注 1:(1) 当 时,由定义1知,
时,由定义1知, 为1-范数DSDD矩阵(即为DSDD矩阵)当且仅当
为1-范数DSDD矩阵(即为DSDD矩阵)当且仅当
 , (2.6)
, (2.6)
(2) 当 时,
时, 为¥-范数DSDD矩阵当且仅当
为¥-范数DSDD矩阵当且仅当
 , (2.7)
, (2.7)
(3) 当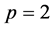 时,
时, 为2-范数DSDD矩阵当且仅当
为2-范数DSDD矩阵当且仅当
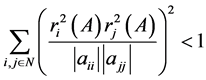 , (2.8)
, (2.8)
(4) 由定理6可知,1-范数DSDD矩阵(即为DSDD矩阵),¥-范数DSDD矩阵,2-范数DSDD矩阵都为非奇异矩阵。
3. p-范数DSDD矩阵与非奇异H-矩阵的关系
非奇异H-矩阵是一类具有重要应用的特殊矩阵。众所周知,双严格对角占优(DSDD)矩阵是非奇异H-矩阵,即p=1时的p-范数DSDD矩阵是非奇异H-矩阵。那么当 时的p-范数DSDD矩阵是否也为非奇异H-矩阵呢?本节我们讨论这个问题。为此首先回忆非奇异H-矩阵的定义。
时的p-范数DSDD矩阵是否也为非奇异H-矩阵呢?本节我们讨论这个问题。为此首先回忆非奇异H-矩阵的定义。
定义4 [2] 。设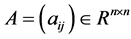 可表示为
可表示为
 , (3.1)
, (3.1)
其中 。若
。若 ,则称
,则称 为M-矩阵;若
为M-矩阵;若 ,则称
,则称 为非奇异M-矩阵。
为非奇异M-矩阵。
定义5 [8] 。设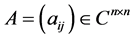 ,如果它的比较矩阵
,如果它的比较矩阵 ,其中
,其中
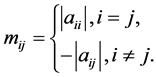 (3.2)
(3.2)
为非奇异M-矩阵,则称 为非奇异H-矩阵。
为非奇异H-矩阵。
引理1 [8] 。设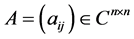 ,则
,则 为非奇异H-矩阵当且仅当对于所有
为非奇异H-矩阵当且仅当对于所有 ,
,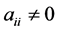 且
且
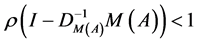 , (3.3)
, (3.3)
其中, 。
。
由引理1,我们可以得到p-范数DSDD矩阵与非奇异H-矩阵的关系。
定理8。设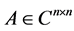 ,如果
,如果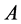 是p-范数DSDD矩阵,则
是p-范数DSDD矩阵,则 为非奇异的H-矩阵。
为非奇异的H-矩阵。
证明:设 是p-范数DSDD矩阵,由定义3知
是p-范数DSDD矩阵,由定义3知 可逆。再由引理1知,只需证明
可逆。再由引理1知,只需证明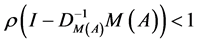 。假若此不等式不成立,即存在
。假若此不等式不成立,即存在 ,使得
,使得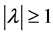 ,则
,则
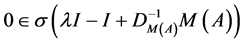 。
。
由于
 ,
,
故
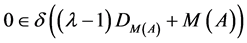 。 (3.4)
。 (3.4)
由于 是p-范数DSDD矩阵,故存在满足
是p-范数DSDD矩阵,故存在满足 的正向量
的正向量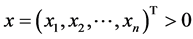 使得(2.4)式成立,即
使得(2.4)式成立,即
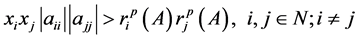 。
。
于是对任意的 有
有
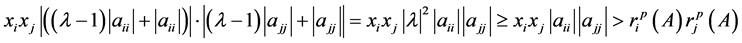 。
。
因为 ,则对任意的
,则对任意的 有
有
 ,
,
 ,
,
所以对任意的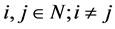 有
有
 。
。
此式表明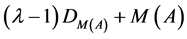 为p-范数DSDD矩阵。由定理6知
为p-范数DSDD矩阵。由定理6知 是非奇异的,因此
是非奇异的,因此 ,这与(3.4)式矛盾。定理得证。
,这与(3.4)式矛盾。定理得证。
4. 矩阵的特征值包含集
我们知道,每一类非奇异矩阵都对应一类矩阵的特征值包含集。由第2节的定理6知p-范数DSDD矩阵是非奇异的。本节就来讨论p-范数DSDD矩阵对应的矩阵特征值包含集。
定理9。设 ,
, ,则对任意满足
,则对任意满足 的正向量
的正向量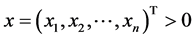 ,有
,有
 , (4.1)
, (4.1)
其中 ;
; 为
为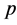 的Hölder补,即
的Hölder补,即 ,
,
证明:用反证法。假若有 ,但
,但 ,则存在满足
,则存在满足 的正向量
的正向量 ,使得对任意
,使得对任意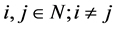 有
有
 ,
,
即矩阵 为p-范数DSDD矩阵。由定理6知,
为p-范数DSDD矩阵。由定理6知, ,这与
,这与 矛盾。故对所有的
矛盾。故对所有的 ,都有
,都有 ,即
,即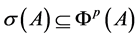 。
。
由定理7可以得到如下特征值包含区域。
定理10。设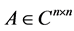 ,
, ,则
,则
 ,
,
其中
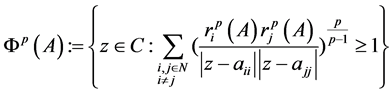 。 (4.3)
。 (4.3)
证明:设 ,
,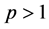 .假若存在
.假若存在 ,使得
,使得 ,则
,则
 。 (4.3)
。 (4.3)
设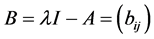 ,由
,由 知,
知,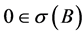 ,故
,故 为奇异矩阵。由
为奇异矩阵。由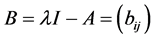 ,
,
易得到
 ,
, ,
,
 ,
, 。
。
于是由(4.3)式可得
 。
。
于是由定理7知矩阵 为p-范数DSDD矩阵。再由定理8知矩阵
为p-范数DSDD矩阵。再由定理8知矩阵 为非奇异的,这与矩阵
为非奇异的,这与矩阵 是奇异的相矛盾,故定理得证。
是奇异的相矛盾,故定理得证。
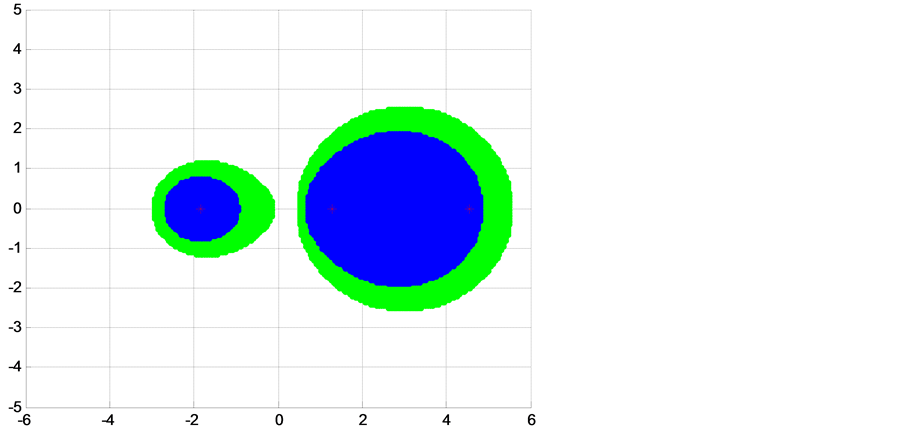
Figure 1. The eigenvalue inclusion region of A for Example 2
图1. 例2中矩阵A的特征值包含区域
5. 数值例子
本节我们给出一个数值例子。该例表明在某些情况下定理10所给的矩阵特征值包含区域含于定理2给出的Brauer-Cassini卵形区域。
例2。设
 。
。
由Matlab可计算出矩阵 的全部特征值为−1.8444,4.5470,1.2974。图1中的绿色部分表示定理2中Brauer-Cassini卵形区域
的全部特征值为−1.8444,4.5470,1.2974。图1中的绿色部分表示定理2中Brauer-Cassini卵形区域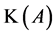 ,蓝色部分表示:当
,蓝色部分表示:当 时,定理10中的矩阵特征包含区域
时,定理10中的矩阵特征包含区域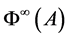 。由图1知,对此例而言定理10给出的特征值包含区域
。由图1知,对此例而言定理10给出的特征值包含区域 比定理2中的Brauer-Cassini卵形区域
比定理2中的Brauer-Cassini卵形区域 要小。
要小。
文章引用
郑巧娟,李耀堂. p-范数双严格对角占优矩阵与新的矩阵特征值包含区域
p-Norm DSDD Matrices and New Eigenvalue Localization Region[J]. 应用数学进展, 2017, 06(03): 367-375. http://dx.doi.org/10.12677/AAM.2017.63042
参考文献 (References)
- 1. Li, B. (1997) Doubly Diagonally Dominant Matrices. Linear Algebra and Its Applications, 261, 221-235. https://doi.org/10.1016/S0024-3795(96)00406-5
- 2. Brauer, A. (1947) Limits for the Characteristic Roots of a Matrix Ⅱ. Duke Math. J., 14, 21-26.
- 3. Kostić, V. (2015) Ongeneral Principles of Eigenvalue Localization via Diagonaldominance. Advances in Computational Mathematics, 41, 55-75. https://doi.org/10.1007/s10444-014-9349-0
- 4. 陈公宁. 矩阵理论与应用[M]. 北京: 科学出版社, 2007.
- 5. Brauer, R. and Corral, C. (2008) Classes of General H-Matrices. Lineaplicatr Algebra and Its Applications, 2008, 1-6.
- 6. 徐仲, 张凯院. 矩阵简明教程[M]. 北京: 科学出版社, 2005.
- 7. 黄廷祝, 钟守铭. 矩阵理论[M]. 北京: 高等教育出版社, 2003.
- 8. Varga, R. (2004) Gersgorin and His Circle. Springer, Berlin. https://doi.org/10.1007/978-3-642-17798-9