Advances in Applied Mathematics
Vol.06 No.09(2017), Article ID:23137,11
pages
10.12677/AAM.2017.69141
Smooth Connection near Singular Points on Subdivision Surfaces
Yuehong Tang1, Sen Li1, Hao Liu2, Yuping Gu1
1Department of Mathematics, College of Science, Nanjing University Aeronautics and Astronautics, Nanjing Jiangsu
2Department of Mechanical and Engineering, College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu

Received: Nov. 30th, 2017; accepted: Dec. 15th, 2017; published: Dec. 22nd, 2017

ABSTRACT
This paper discusses G2 smooth connection near singular points on subdivision surfaces. A shape adjustable Catmull-Clark subdivision algorithm is present by introducing subdivision shape adjustment parameter . Based on this, aimed at the singular points in subdivision surface, based on the 2-ring of the singular points as control mesh, adopting the method of cyclic mapping, this paper proposes a G2 surface modeling method which is shape-adjustable. Then we can get the explicit solution of the Bezier control points. Compared with existing methods, the generated surface not only achieves the G2 continuous at singular points, but solves the problem of the curved surface design to be adjustable. The algorithm process and data structure are present. Corresponding examples are also given in this paper.
Keywords:Subdivision Surfaces, Geometric Continuity, Singular Points
细分曲面奇异点处的光滑过渡
唐月红1,李森1,刘浩2,古玉屏1
1南京航空航天大学理学院数学系,江苏 南京
2南京航空航天大学机电学院机械工程系,江苏 南京

收稿日期:2017年11月30日;录用日期:2017年12月15日;发布日期:2017年12月22日

摘 要
首先通过引入形状调节参数 给出了一种形状可调的C-C细分方法,基于该理论,针对细分曲面中的奇异点,本文以奇异点处的2-环作为控制网格,采用循环映射的方法,提出了一种形状可调的G2曲面造型方法,得到Bézier控制点的显式解。与以往的方法相比,生成的曲面不仅在奇异点处达到G2连续,而且解决了曲面设计的可调性问题。本文给出了算法流程和相关数据结构,也给出了相应的实例进行验证。
关键词 :细分曲面,二阶几何连续,奇异点

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
细分曲面与NURBS曲面是现代工业的两大造型技术,细分曲面克服了NURBS曲面处理任意拓扑结构存在的困难,成为有效的建模手段之一。在曲面造型技术中奇异点的出现始终是无法避免的,由于奇异点的存在,最终得到的曲面会出现“褶皱”等现象,严重影响曲面的质量,尤其是在工业产品的设计中,如果奇异点的处理不恰当,会使产品无法投入使用,因此,奇异点的处理技术成为曲面造型的关键点。传统的细分方法的奇异点处仅仅满足 连续,为了构造出 连续的曲面,人们进行了很多的探索。2009年,剑桥大学的Thomas J. Cashman [1] 等人采用任意次数的B样条曲线曲面给出了一种对称的非均匀细分算法,并且将该算法推广到曲面,得到了一种奇数次的对称非均匀细分算法,但是该算法在奇异点处没有具体说明,而且只针对奇数阶的情况;后来,Thomas J. Cashman和Malcolm A. Sabin等人 [2] 设计了新的细分格式来处理非均匀细分算法中的奇异点,但是结果并不理想,具有较差的局部性;刘浩 [3] 等人利用流行方法和细分方法构造出 连续的自由型曲面,实现了流行曲面和Catmull-Clark细分曲面的融合,然而,在构造 边域曲面片时没有考虑奇异点的位置信息。本文在Charles Loop [4] 等人研究的基础上,进行了以下改进:(1) 引入了一种形状可调的Catmull-Clark细分方法,将该方法作为C-C细分的前置方法,对曲面进行“混合细分”,使最终的拟合曲面具有一定的可调性;(2) 采用循环映射对奇异点周围的曲面片进行处理时,得到的循环矩阵也含有参数 ,使每一个曲面片都具有可调性;(3) 给出了双七次Bézier控制点的具体位置以及循环方程组的显式解,得到每一个曲面片的显示表达式,并给出了奇异点处的 填充结果。
2. 一种形状可调的C-C细分曲面
经典的Catmull-Clark细分基于双三次均匀B-样条,在给定初始控制网格的情况下,生成的结果曲面也就唯一确定,不具有可调性。而在实际应用中,往往大多时候生成的结果曲面不能直接满足要求,需要进行一定的调整。因此,为了增强曲面设计的灵活性和可调性,我们将曲线的可调性 [5] 推广到曲面的可调性,重新设计几何规则和拓扑规则。
对于任意拓扑形状的控制网格,新的细分规则还是由两部分组成:几何点的产生和拓扑结构的建立。
(1) 几何点的产生
给定一个初始网格 ,经过 次改进的Catmull-Clark细分后得到的控制网格为 。考虑 上度为 的顶点 的局部网格,它的邻域由 个共边顶点 和 个共面顶点 组成,则第 次细分后产生的新面点、新边点和新顶点为:
新面点(F-点):用面上所有顶点的均值表示
新边点(E-点):用相邻两面上的新面点均值的 倍与对应边两端点的均值的 倍的和来表示
新顶点(F-点):用对应顶点、新面点与其周围一些点的线性组合可以表示为
其中 表示所有与旧顶点相邻的面上新面点的均值, 表示所有交于旧顶点的边的中点的均值, 为对应顶点的度数。同时, ,且设 , 。
(2) 拓扑结构的建立
与经典Catmull-Clark的拓扑规则相同,连接每一个新面点与其周围的新边点;连接每一个新顶点与其周围的新边点。
从曲面的细分规则可以推出,给定原控制点 则细分后的曲面片可表示为 ,其中 , ,相应的参数调节矩阵为
3. 细分曲面奇异点处的G2连续性
本节通过改进Charles Loop [4] 的理论给出了含有奇异点的 重建方法。首先,对初始控制网格进行“混合细分”,即先采用形状可调的C-C细分方法进行细分然后再用经典的C-C细分,目的是为了保证曲面片具有B样条边界;其次,在“混合细分”的基础上,以奇异点处的2-环作为控制网格,采用循环映射的方法得到了二阶连续的约束方程组;最后,利用循环矩阵和能量函数优化方法给出了 填充 边洞时,Bézier控制点的显式解,不仅使奇异点周围曲面片之间满足 ,并且和Catmull-Clark细分曲面实现 拼接,得到整体 连续的曲面。
3.1. 二阶几何连续条件
定义1:两曲面 和 沿公共连接线 具有 连续的充要条件 [6] 是两曲面之一可以重新参数化,以至于它们沿公共连接线为 连续的。如 重新参数化为 ,使得
根据上述定义可知,给定两个曲面片 和 : ,沿公共边界 二阶几何连续的充要条件是存在函数 使得下列表达式沿 成立:
3.2. 初始控制网格的“混合细分”
对于任意拓扑形状的散乱点集得到的控制网格,采用本文第1节给出的形状可调的C-C细分算法,对网格进行细分,得到的网格曲面可以表示为
令 , 为双三次系数矩阵,则第 个曲面片对应的系数矩阵为 ,相应的参数调节矩阵为
为了保持双三次样条边界,必要时可以在此基础上重新进行Catmull-Clark细分,该过程称为“混合细分”。通过“混合细分”将奇异点从正则网格中隔离出来,构造出奇异点的 边洞,对于正则处已经满足二阶连续,下面要做的就是如何在保证二阶几何连续的情况下填充 边洞并且与周围的曲面片拼接后曲面整体达到二阶连续。如图1所示。
在图1中,与奇异点直接相邻的边,称为内部边界;与奇异点间接相邻的边称为外部边界。要使最后整张曲面为 连续,要求曲面片内部边界之间的拼接是 且外部边界与Catmull-Clark曲面片之间的拼接也满足 。经过“混合细分”后,构造出奇异点的二环,如下图2所示。
对于 边洞的填充,本文构造了双七次B-样条曲面片进行填充,令
则
若 为曲面片 和 之间的参数化矩阵,则由二阶几何连续性定义可以得到
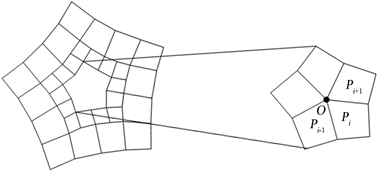
Figure 1. N-sided hole formed by mingle subdivision
图1. 混合细分产生的n边洞
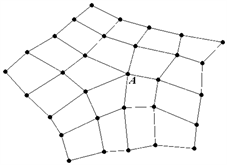
Figure 2. 2-ring around singular vertex on mesh
图2. 混合细分后奇异点的二环
那么,具有公共顶点的 个曲面片 ( ),相邻的曲面片之间满足几何连续和循环条件,则 个具有公共顶点的曲面片之间满足如下关系
从上式推得
要使最后整张曲面为 连续,要求曲面片内部边界之间的拼接是 且外部边界与Catmull-Clark曲面片之间的拼接也满足 。
3.2.1.内部边界的连续性
首先,定义内部边界的相关映射为 ,令
是以原点为中心 为单位的一个逆时针旋转变换
则可以得到 。于是,对于 价奇异点周围的曲面片 有
(1)
成立, , 为对应变换 , 的矩阵,并且 。
对于带有内部边界的曲面片 和 达到二阶几何连续,则需要满足下面三个条件
(2)
(3) (4)
令双七次张量积曲面片 ,则对于 边洞的第 和 个曲面片 和 可以得到 、 、 、 、 、 、 、 、 、 ,将上述结果代入(2)可以得到
代入(3)可得
.
为表示简便,在这里系数 表示
对于系数 表示
以此类推,代入(4)也可以得到8个方程。因此,可以得到24个约束方程,其中含有8个独立方程自动满足循环条件,因此,实际上得到16个约束方程。
3.2.2. 外部边界的连续性
外部边界指的是在奇异点周围,不以奇异点为顶点,并且在拼接过程中与周围曲面片共有的边。在这里可以将外部边界的两个端点分为两类:第一类是与奇异点相邻的点;第二类是与奇异点相对的点。定义映射 ,其中 为对应奇异点的价。对于第一类点,令
,
对应的链式规则矩阵分别为 , 为 的块对角矩阵,其中,
,
对于第一类点有
令 ,则 ,对于第二类点有
由上述两个式子可以推得
其中, ,又由对称性可得 。
在奇异点周围可以得到 个“混合细分”的双三次B-样条曲面片,对于外部边界,通过运用双三次节点插入算子,将B样条转化为 个Bernstein形式的双三次Bézier曲面片的控制点
,
其中 ,
为“混合细分”矩阵。
对于奇异点处的第 个曲面片,有
则Bézier曲面片的表达式
要使外部边界 满足二阶几何连续只需要满足下面条件即可
类似于内部边界,可以推得
、 、 、 、 、 、 和 。同时,由已知条件可以得到
对于外部边界 连续性条件,每个方程的化简计算后次数不超过7次,含有8个系数,由对应系数相等,可以得到24个方程,同理,对于外部边界 也可以得到24个方程。对于n价的奇异点则产生48n个约束方程。对于曲面片 和 的内部边界,由连续性条件可以得到24个约束方程,但是当 时, 和 所确定的9个二阶混合偏导自动满足约束条件,与外部边界的二阶连续性条件重复,因此,对于 价的奇异点则产生16n个约束方程。这样,一共得到了64n个方程,对于价为 的奇异点,双七次曲面环恰好有64n个未知数,因此可以求得该方程解即所求的控制顶点。
3.3. Bézier控制点的求解
对于简单的公式,可以直接以文本方式输入;对于复杂的公式,可以考虑使用公式编辑器,或者将公式制作成图片后插入文中。编辑公式的过程中要特别注意减号与连字符的区别,前者较长,后者较短。令双七次曲面片控制顶点的系数矩阵为 ,则对应的第 个曲面片的系数矩阵为 ,为了保证曲面片整体的二阶连续性,则需要满足如下条件
其中, 为循环矩阵, 为双七次曲面片控制顶点,矩阵 对应图2二环中第 个曲面片的样条顶点。对于循环矩阵 [7] ,它的全部特征根为 ,其中 ,并且 相似于对角阵 。
为了使二次能量函数 [8] 最小,接下来采用Lagrange乘子法 [9] ,可将约束条件转化为下列形式
对于第 个块方程,有
其中,对于第 个方程,只有 的系数为 ,其余的均为0。
然后采用傅里叶变换 [10] (DFT),令 ,其中, , ,
Euler系数 , 则有
(5)
其中, 。
将 代入(5)式即可得到 。
于是上式可转化为 解得 (其中 ),求得 后再利用傅里叶逆变换(IDFT),将 代入(5)式即可反求出相应的双七次控制顶点 。
4. 曲面造型结果
下面是运用本文的算法对某品牌汽车进行样条重建的实例,对工业设计中汽车车身出现的5-边洞和3-边洞进行局部填充,图3(a)和图4(a)是汽车局部网格图;图3(b)和图4(b)是网格的控制顶点图,为了清楚进行了一些旋转;图3(c)和图4(c)是奇异点附近的网格填充图。整个填充过程如图3和图4所示。
下面是采用本节的方法对汽车局部模型进行曲面造型的结果。该汽车局部散乱点为1452个,“混合细分”后的四边形网格有323个,图中分给出了10个奇异点多变行动填充。图5(a)为“混合细分”得到的四边形控制网格,图5(b)为奇异点的二环结构,图5(c)经过双七次样条拟合后,奇异点周围各曲面片之间满足 连续,具体过程如图5所示。
 (a)3价奇异点局部网格
(a)3价奇异点局部网格
 (b)3奇异点的控制顶点
(b)3奇异点的控制顶点
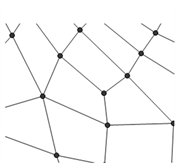 (c)3价奇异点的拟合
(c)3价奇异点的拟合
Figure 3. 3-sided hole filling
图3. 3-边洞的填充
 (a)5价奇异点局部网格
(a)5价奇异点局部网格
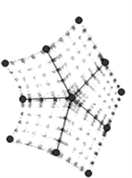 (b)5奇异点的控制顶点
(b)5奇异点的控制顶点
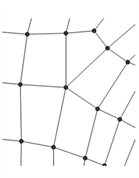 (c)5价奇异点的拟合
(c)5价奇异点的拟合
Figure 4. 5-sided hole filling
图4. 5-边洞的填充
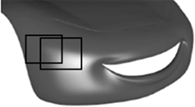 (a) 进行“混合细分”
(a) 进行“混合细分”
 (b) 对n边洞进行填充
(b) 对n边洞进行填充
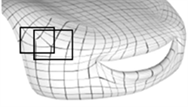 (c) G2连续曲面
(c) G2连续曲面
Figure 5. Surface modeling with G2 continuity
图5. G2连续曲面造型
5. 小结
本文致力于细分曲面造型中奇异点处的 连续性研究,给出了奇异点处的 算法,主要给出了细分曲面中奇异点处的 重建算法,主要分为三个部分:第一,给出了形状可调的C-C细分算法;第二,具体给出了奇异点处的 重建方法;第三,给出了奇异点处3边洞和5边洞的填充结果。增加了工业设计中细分曲面的可调性,逐步拓宽了应用范围。
基金项目
国家自然科学基金(51175248/E050603);南京航空航天大学基本科研业务费资助(NZ2013201)。
文章引用
唐月红,李 森,刘 浩,古玉屏. 细分曲面奇异点处的光滑过渡
Smooth Connection near Singular Points on Subdivision Surfaces[J]. 应用数学进展, 2017, 06(09): 1163-1173. http://dx.doi.org/10.12677/AAM.2017.69141
参考文献 (References)
- 1. Cashman, T.J. (2010) NURBS-Compatible Subdivision Surfaces. University of Cambridge Compute Laboratory, 773-873.
- 2. Cashman, T.J., Dodgson, N.A. and Sabin, M.A. (2009) Selective Knot Insertion for Symmetric, Non-Uniform, Refine and Smooth B-Splines Subdivision. Computer Aided Geometric Design, 26, 472.
https://doi.org/10.1016/j.cagd.2008.11.002 - 3. 刘浩, 廖文和. 用C-C细分方法和流行方法构造G2连续的自由型曲面[J]. 计算机辅助设计与图形学学报, 2005, 17(4): 644-649.
- 4. Loop, C. (2004) Second Order Smoothness over Extraordinary Vertices. Proceedings of the 2004 Eurographics/ACM Siggraph Symposium on Geometry Processing, 71, 165- 174.
https://doi.org/10.1145/1057432.1057454 - 5. 王卫民, 罗国明, 张纪文, 等. 一种可调的Catmull-Clark细分曲面[J]. 工程图学学报, 2002, 23(3): 115-121.
- 6. 王国谨, 汪国昭, 郑建民. 计算机辅助几何设计[M]. 北京: 高等教育出版社; 海德堡: 施普林格出版社, 2001.
- 7. 邓群毅. 关于循环矩阵的推广及应用[D]: [博士学位论文]. 宁波: 宁波大学, 2012.
- 8. Eck, M. and Hoop, H. (1996) Automatic Reconstruction of B-Spline Surfaces of Arbitrary Topological Type. Computer Graphics, 30, 325-334.
https://doi.org/10.1145/237170.237271 - 9. Yong, J.-H. and Cheng, F.H. (2005) Adaptive Subdivision of Cat-mull-Clark Subdivision Surfaces. Computer-Aided Design & Applications, 2, 253-261.
https://doi.org/10.1080/16864360.2005.10738373 - 10. Li, W.-X., Zhang, D. and Xu, Z.-Q. (2002) Palmprint Recognition Based on Fourier Transform. Journal of Software, 13, 879-886.